Рабочеподобное» обучение

Этот несколько необычный термин используется для случая, когда эмпирические данные являются итогом серии действий, каждое из которых происходит в ситуации, соответствующей значению и сопровождается получением некоторой совокупности данных наблюдения и принятием решения , причем выбирается из того же множества решений U, что и решение 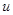в рабочей ситуации. При таком способе получения эмпирических данных может встретиться несколько характерных случаев.

1). Потери для всех определяются той же функцией потерь, что и в рабочей ситуации, но несущественны, а сами решения выбираются независимо от нас. Это соответствует использованию чужого опыта в ситуациях, аналогичных интересующей нас рабочей ситуации, о котором мы получаем информацию, но за который в каж­дом случае принятия решения расплачивается кто-то другой.

Очевидно, что этот случай не отличается принципиально от про­стого обучения, поскольку платить за последствия приходится только один раз - в рабочей ситуации. Может измениться только содержание информации, заключенной в .

Наряду с рассмотренным ранее, каждая из составляющих может содержать в себе решение и величину потерь , соответствующую этому решению и значению параметра (известному либо нет), ха­рактеризующему -ю ситуацию. Эти сведения довольно содержательны с точки зрения возможности решения задач синтеза систем, когда априори функция потерь 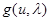, то есть критерий качества системы, не задана или известна неполностью. Эмпирические данные { 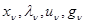} для различных позволяют с той или иной степенью полноты восста­новить зависимость функции потерь или апостериорного риска от своих аргументов для принятия оптимального решения 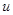в рабочей ситуации. В отношении постановки задачи отыскания правила решения в этом случае имеет место все сказанное в п. 3.3.1 в.

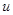2). Для всех и в рабочей ситуации решения и выбираются независимо, причем решение выбирается из условия минимума ожидаемых потерь для функции , а решение 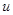- для функ­ции 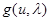. Функции могут быть как одинаковыми с 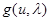, так и различными. Независимый выбор решений означает требование ло­кальной оптимальности для каждого элемента серии и ра­бочей ситуации. Любая из составляющих может иметь то же содержание, что в п. 1, то есть наряду с данными подобными х, содержать сведения о , и . Довольно часто совокупность { } пред­ставляет собой упорядоченную последовательность. В этом случае каж­дое очередное решение может зависеть от всех , подобно тому, как решение 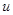в рабочей ситуации может использовать х и .

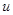3). Следующим характерным случаем является такой, когда после­довательность решений и решение в рабочей ситуации объединены единой целью, количественным выражением которой является функция потерь , и требуется минимизировать общий риск, соответствующий этой функции потерь. При этом решения и 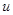уже не могут приниматься независимо, а выбор частных решений в процессе набора эмпирических данных должен обеспечивать как уменьшение риска в каждой -й си­туации, так и его минимальное значение в конечной рабочей ситуации.

Обычно серия представляет в этом случае упорядочен­ную последовательность, что соответствует возможности выбора реше­ния , зависящего от всех предыдущих значений 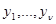и соответственно . Составляющие эмпирической последовательности могут иметь ту же природу, что и выше, а сама последовательность решений представляет собой многоша­говый процесс, описанный в §2.7.

Два наиболее типичных случая задания меры потерь соответст­вуют аддитивной функции потерь, когда

(3.3.6)

ифункции потерь, не зависящей от { }, то есть

. (3.3.7)

Последняя сосредоточивает все внимание при выборе решений в процессе набора эмпирических данных на обеспечении минимальных потерь в рабочей ситуации. Естественно, что для функции потерь (3.3.7) зависимость в выборе решений будет только тогда, когда эмпириче­ские данные действительно имеют ценность, то есть существует априорная неопределенность, связанная с незнанием или неполным знанием функ­ции правдоподобия 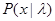и априорного распределения 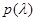, или имеется статистическая зависимость между х и { }. В против­ном случае, как следует из общих выражений гл. 2, многошаговый про­цесс принятия решений распадается на отдельные независимые шаги и выбор последовательности решений { } не влияет на выбор решения 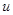в рабочей ситуации.

В заключение отметим, что, как и в разд. 3.3.1, при наличии эмпи­рических данных может быть различная степень априорной неопреде­ленности в отношении статистического описания х, и { } - от полного незнания их распределений вероятности до полного стати­стического описания; и как и в предыдущих случаях, чрезвычайно удобно параметрическое описание с использованием имеющихся физических представлений и соответствующих им закономерностей.

Дата добавления: 2015-09-03