Принцип асимптотической оптимальности

В практических задачах синтеза в условиях априорной неопреде­ленности часто характерно наличие большого объема данных наблюде­ния х, которые могут включать в себя (см. гл. 3) информацию о прошлом опыте, данные обучения, эмпирическую статистику и т. д. При этом в случае полного статистического описания значительная часть этих дан­ных оказалась бы избыточной, зато в условиях априорной неопределен­ности такая избыточность является в какой-то степени компенсацией за отсутствие четкого и полного статистического описания задачи. 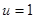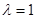Поясним это на примере простой задачи двухальтернативного решения ( или , или , , 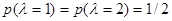) на основа­нии данных наблюдения , образующих совокупность независимо распределенных величин. Пусть

(4.3.3)

где - некоторый параметр плотности вероятности . Статистическое описание (4.3.3) соответствует, например, случаю, когда фактически ре­шение должно быть принято на (n+ 1)-м шаге по результатам наблюде­ния , а предыдущая серия { }наблюдалась в условиях точно известной ситуации (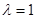) и может рассматриваться в качестве обучаю­щей последовательности. Возможная априорная неопределенность в дан­ной задаче связана с незнанием параметра , из-за чего статистическое описание (4.3.3) становится неполным.

Если априорная неопределенность отсутствует - параметр извес­тен - оптимальное правило решения имеет вид (гл. 2): принимается 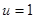, если

. (4.3.4)

Это правило, естественно, зависит только от , а все остальные дан­ные наблюдения являются избыточными. Если параметр неизвестен, то знание { }очень существенно, поскольку оно может быть использовано для уменьшения априорной неопределенности из-за неиз­вестности .

При этом по крайней мере интуитивно ясно, что чем больше объем подобных «избыточных» данных (в рассматриваемом примере этот объ­ем характеризуется числом наблюдений ), тем меньше влияние апри­орной неопределенности. Поэтому можно надеяться, что при увеличении объема и улучшения качества наблюдаемых данных х можно получить решение такого же качества, как если бы априорная неопределенность отсутствовала и распределение нам было бы известно точно. Отсюда
логически вытекает принцип асимптотической оптимальности, который может быть сформулирован следующим образом:

- более предпочтительным является такое правило решения 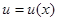, для которого средний риск с увеличением объема данных наблюдения стремится к минимальному байесову риску
для всех P равномерно.

Само правило решения 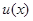, удовлетворяющее этому требованию, является асимптотически равномерно наилучшим решением, а при огра­ниченном, но большом объеме данных наблюдения х - приближенно равномерно наилучшим. Принцип асимптотической оптимальности имеет очевидный недостаток - он не определяет вполне однозначно и оставляет открытым вопрос, какое из асимптотически оптимальных пра­вил решения лучше при ограниченном объеме данных наблюдения. Однако столь же очевидна и его полезность - он позволяет отклонить как неудовлетворительные те правила, которые даже асимптотически су­щественно отличаются от оптимального байесова.

Дата добавления: 2015-09-03