
Читайте также:
|
Найти пределы, используя правило Лопиталя
1) 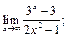 2)
2) 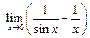 .
.
Раскрытие неопределенных выражений вида  .
.
1) 
| Определим вид неопределенного выражения. Правило Лопиталя можно применять при неопределенностях вида  . .
| |
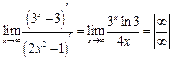
| После вычисления производных неопределенное выражение сохранилось. | |
= 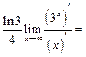 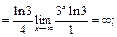
| Применим правило еще раз. Неопределенность раскрыта, получен ответ. | |
2) 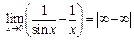 = = 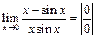
| Приведение к общему знаменателю позволяет получить неопределенное выражение, которое можно раскрывать с помощью правила Лопиталя. | |
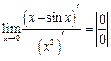 = = 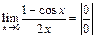 ; ;
| Перед вычислением производных учтем, что 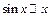 при при  , и , и 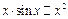 . .
| |
 = =  .
Здесь вместо повторного применения правила Лопиталя произведена замена эквивалентными бесконечно малыми величинами.
Задача 5.
Методами дифференциального исчисления исследовать функцию и построить ее график .
Здесь вместо повторного применения правила Лопиталя произведена замена эквивалентными бесконечно малыми величинами.
Задача 5.
Методами дифференциального исчисления исследовать функцию и построить ее график
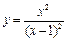 .
Решение. .
Решение.
| ||
Рассмотрим аналитическое выражение, задающее функцию: 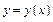 и определим следующие характеристики.
и определим следующие характеристики.
Область
допустимых значений (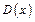 , ОДЗ) , ОДЗ)
| Знаменатель функции обращается в нуль в точке  . ОДЗ данной функции . ОДЗ данной функции 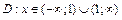 . .
| |||
Нули функции и точки пересечения с осью  . .
| График пересечет ось ординат  при значении абсциссы при значении абсциссы 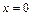 , ,  , поэтому график функции проходит через начало координат: , поэтому график функции проходит через начало координат: 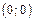 . .
| |||
| Четная, нечетная, общего вида | 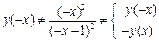 , значит данная функция является функцией общего вида. , значит данная функция является функцией общего вида.
| |||
| Исследование точек разрыва и поведения функции на границах ОДЗ | Исследуем вид разрыва в точке  . .
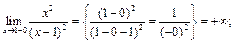
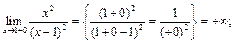 В точке
В точке  имеется разрыв 2-го рода и вертикальная асимптота функции имеется разрыв 2-го рода и вертикальная асимптота функции  . .
| |||
| Наклонные игоризонтальные асимптоты функции |  , где , где  и и 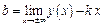 . .
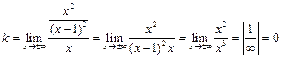 ; ;
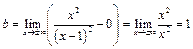 . Данная функция имеет горизонтальную асимптоту . Данная функция имеет горизонтальную асимптоту 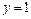 . .
| |||
| Точки возможных экстремумов - критические точки |  ; ;  ; преобразованное выражение производной: ; преобразованное выражение производной: 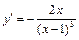 . Критические точки: . Критические точки:
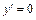 при при  и и
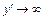 при при 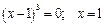 (точка разрыва). (точка разрыва).
| |||
 7 7
| Интервалы возрастания / убывания (монотонности). Обозначения: - возрастает, ¯ - убывает | Критическая точка и точка разрыва разделяют интервалы монотонности функции. Определим знаки первой производной на каждом интервале. | ||
Экстремумы (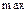 / / 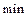 ) )
| Теперь можно сделать заключение об экстремуме функции в точке 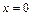 . При переходе через эту точку первая производная меняет знак, убывание функции сменяет возрастание, поэтому это точка минимума функции: . При переходе через эту точку первая производная меняет знак, убывание функции сменяет возрастание, поэтому это точка минимума функции:  .
В точке .
В точке  не существует экстремума, так как это точка разрыва второго рода. не существует экстремума, так как это точка разрыва второго рода.
| |||
| Точки возможного перегиба графика функции |  Найдем точки возможного перегиба графика функции:
Найдем точки возможного перегиба графика функции:  при при 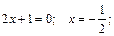 и и
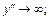 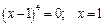 (точка разрыва). (точка разрыва).
| |||
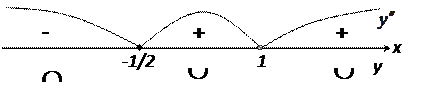 10 10
| Интервалы выпуклости / вогнутости. Обозначения: È - вогнута, Ç - выпукла | Две найденные точки разделяют интервалы выпуклости / вогнутости функции. Определим знаки второй производной на каждом интервале. | ||
| Точки перегиба | Теперь можно сделать заключение о точке перегиба функции. При переходе через точку  вторая производная меняет знак, выпуклость функции меняется на вогнутость, поэтому это точка перегиба функции: вторая производная меняет знак, выпуклость функции меняется на вогнутость, поэтому это точка перегиба функции: 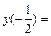 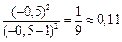 . .
| |||

Построение графика функции рекомендуется начинать с построения всех асимптот и всех точек, через которые проходит график функции, которые получены в процессе исследования.
Дата добавления: 2015-08-21; просмотров: 44 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 3. | | | Желаю Вам всегда быть красивыми, здоровыми, чтобы никогда Вам не попадался товар, вредящий вашей красоте, здоровью и жизни! |