Задача 1. Линейная алгебра

Часть 1

Линейная алгебра. Аналитическая геометрия

Задача 1.

Вычислить определитель .

Решение.

Способ 1.

Вычислим определитель методом понижения порядка.

Выносим за знак определителя из четвертого столбца общий множитель :

,

, а затем будем последовательно умножать третью строку на и складывать соответственно с первой и со второй строками. Имеем

.

Далее полученный определитель раскладываем по элементам третьего столбца

.

Получим определитель третьего порядка, который можно вычислить по правилу Саррюса или подобным приемом свести к вычислению одного определителя второго порядка. Для этого последовательно умножим элементы первого столбца на и прибавим соответственно к элементам второго и третьего столбцов. Получаем

.

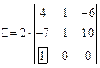Полученный определитель раскладываем по элементам третьей строки, имеем:

.

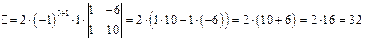Способ 2.

Вычислим определитель методом приведения его к треугольному виду.

Выполним следующие операции. Выносим за знак определителя из четвертого столбца общий множитель , а затем переставим местами первую и четвертую строки – определитель меняет свой знак на противоположный:

.

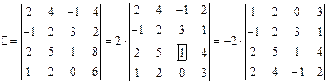Далее, первую строку определителя сложим со второй, эту же строку, умноженную на с третьей, на с четвертой строкой. В итоге получим определитель, который равен исходному:

.

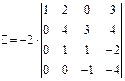Вторую строку определителя умножим на 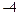и сложим с третьей:

.

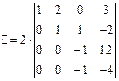Из четвертой строки вычтем третью:

.

Определитель треугольного вида равен произведению элементов его главной диагонали. Имеем

.

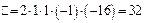Дата добавления: 2015-08-21