
Читайте также:
|
Решите систему уравнений тремя способами:
1) по формулам Крамера;
2) с помощью обратной матрицы (матричным методом);
3) методом Жордана - Гаусса.
Выполните проверку.
Решение.
1) Если определитель  системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, которое может быть найдено по формулам Крамера
системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, которое может быть найдено по формулам Крамера
 ,
,
где  определитель системы,
определитель системы,
 вспомогательные определители, которые получаются из определителя
вспомогательные определители, которые получаются из определителя  заменой столбца из коэффициентов соответственно при
заменой столбца из коэффициентов соответственно при  столбцом свободных членов.
столбцом свободных членов.
Определитель системы равен
 .
.
Вычислим вспомогательные определители:
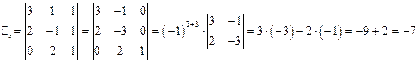 ;
;
 ;
;
 .
.
По формулам Крамера найдем:

2) Систему линейных алгебраических уравнений можно записать в виде матричного уравнения:
 ,
,
где  матрица системы;
матрица системы;  столбец неизвестных;
столбец неизвестных; 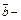 столбец свободных членов.
столбец свободных членов.
Если матрица  невырожденная, то решение системы определяется по формуле:
невырожденная, то решение системы определяется по формуле:
 ,
,
где  обратная матрица.
обратная матрица.
Для данной системы

столбец неизвестных  , столбец свободных членов
, столбец свободных членов  .
.
Найдем обратную матрицу  по формуле
по формуле
 ,
,
где  определитель матрицы
определитель матрицы  ,
,
 союзная матрица, которая получается из матрицы
союзная матрица, которая получается из матрицы  заменой всех ее элементов соответствующими им алгебраическими дополнениями.
заменой всех ее элементов соответствующими им алгебраическими дополнениями.
Определитель матрицы
 .
.
Вычислим алгебраические дополнения для элементов матрицы  по формуле
по формуле
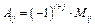 ,
,
где  минор элемента
минор элемента  .
.
 ,
,  ,
,  ,
,
 ,
,  ,
, 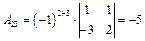 ,
,
 ,
,  ,
,  .
.
Составим союзную матрицу
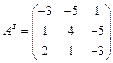 .
.
Обратная матрица будет равна
 ,
,
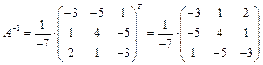 .
.
Проверим правильность нахождения обратной матрицы, используя соотношение  .
.
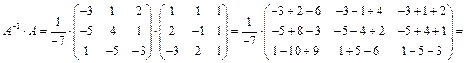
 .
.
Теперь можно получить решение системы в матричном виде:
 .
.
 .
.
3) Метод Жордана – Гаусса (метод полного исключения неизвестных).
Пусть задана СЛАУ  . Запишем ее расширенную матрицу
. Запишем ее расширенную матрицу 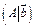 . Каждому элементарному преобразованию строк расширенной матрицы соответствует аналогичное преобразование уравнений в исходной СЛАУ.
. Каждому элементарному преобразованию строк расширенной матрицы соответствует аналогичное преобразование уравнений в исходной СЛАУ.
Элементарные преобразования в расширенной матрице:
1) перемена местами строк;
2) перемена местами столбцов с запоминанием, какому неизвестному соответствует каждый столбец;
3) умножение (деление) строки на ненулевую постоянную;
4) прибавление к любой строке линейную комбинацию других строк;
5) вычеркивание одной из двух пропорциональных (равных) строк;
6) вычеркивание нулевой строки.
Эти преобразования не меняют множество решений системы.
Если элементарными преобразованиями строк матрица 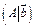 переведена в матрицу
переведена в матрицу  , то столбец
, то столбец  есть решением системы линейных уравнений
есть решением системы линейных уравнений  .
.
Составим расширенную матрицу 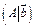 и проведем необходимые элементарные преобразования:
и проведем необходимые элементарные преобразования:



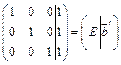 .
.
 .
.
Проверка.
Подставив полученное решение в систему, убедимся в правильности полученного решения:

Дата добавления: 2015-08-21; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 1. | | | Задача 6. |