Задача 18.

Построить кривую, заданную уравнением, приведя его к каноническому виду. Определить:

1) для окружности – координаты центра и радиус;

2) для эллипса – координаты центра, полуоси, координаты фокусов, эксцентриситет, уравнения директрис;

3) для гиперболы – координаты центра, действительную и мнимую полуоси, координаты фокусов, эксцентриситет, уравнения директрис, уравнения асимптот;

4) для параболы – координаты вершины, параметр параболы, координаты фокуса, уравнение директрисы.

Решение.

а) Исследуем кривую второго порядка, заданную своим уравнением .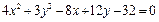

В этом уравнении второго порядка коэффициенты при квадратах переменных имеют одинаковый знак. Значит, уравнение относится к эллиптическому типу. Выделяя полные квадраты по обоим переменным, получаем

,

,

,

,

.

Точка центр эллипса. малая полуось, большая полуось эллипса. Так как , то фокусы лежат на вертикальной оси симметрии. Поэтому , а эксцентриситет (отношение фокального расстояния эллипса к его большой оси) . Координаты фокусов: . Уравнения директрис: ; для данного эллипса: .

Рисунок

б) В уравнении кривой второго порядка коэффициенты при квадратах переменных имеют противоположный знак. Поэтому уравнение относится к гиперболическому типу. Выделяя полные квадраты по обоим переменным, получаем

,

,

,

,

.

Уравнение задает сопряженную гиперболу с центром в точке , действительной полуосью , мнимой полуосью . При этом , а эксцентриситет (отношение фокального расстояния гиперболы к ее действительной оси) . Координаты фокусов: . Уравнения директрис: ; для данной гиперболы: . Уравнения асимптот: ; для данной гиперболы: .

Рисунок

в) Уравнение кривой второго порядка относится к параболическому типу, поскольку содержит только одно слагаемое с переменным в квадрате. Выделяя полный квадрат по , получаем

,

,

,

,

,

.

Это парабола с горизонтальной осью симметрии, для которой параметр , а . Вершина параболы находится в точке . Координаты фокуса: ; для данной параболы . Уравнение директрисы ; для данной параболы .

Рисунок

Дата добавления: 2015-08-21