Задача 6. Исследовать на совместность и в случае совместности найдите общее решение методом

Исследовать на совместность и в случае совместности найдите общее решение методом Жордана – Гаусса и одно частное решение системы. Выполните проверку.

Решение.

Используем метод Жордана – Гаусса (метод полного исключения). Составим расширенную матрицу неоднородной СЛАУ и проведем необходимые элементарные преобразования строк:

.

, где число неизвестных. Система совместна, имеет бесчисленное множество решений. Базисный минор 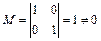. Число свободных переменных . Пусть базисные переменные, свободные переменные.

Исходная система равносильна системе из двух уравнений

Общее решение неоднородной СЛАУ представим так:

.

Полагая, например, , найдем частное решение:

.

Непосредственной подстановкой в систему частного решения убедимся в его правильности:

Дата добавления: 2015-08-21