Задача 11. Вычислите площадь параллелограмма, построенного на векторах и

Вычислите площадь параллелограмма, построенного на векторах и , если .

Решение.

Площадь параллелограмма, построенного на векторах 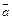и , равна

.

Согласно свойствам векторное произведение векторных многочленов производится по тем же правилам, что и умножение алгебраических многочленов. Тогда, используя антикоммутативность векторного произведения и тот факт, что векторное произведение вектора на самого себя равно нуль – вектору, получим

.

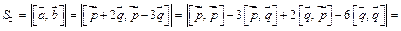
Задача 12.

Вычислить 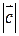, если .

Решение.

.

Задача 13.

Найти вектор , ортогональный векторам и и удовлетворяет условию .

Решение.

Вектор коллинеарен векторному произведению , следовательно, . Поскольку

,

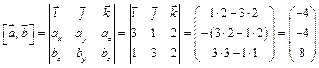то

.

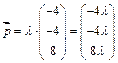Так как , то

,

,

.

Теперь можно определить координаты вектора

.

Дата добавления: 2015-08-21