Построение математической модели объекта по экспериментальной переходной характеристике.

Задача построения математической модели включает в себя несколько этапов:

1. Выбор аппроксимирующей передаточной функции, дающей приемлемую модель объекта для проектирования АСР с типовыми регуляторами;

2. Определение параметров модели, обеспечивающих совпадение аппроксимируемой и аппроксимирующих переходных характеристик согласно выбранному критерию приближения;

3. Оценка точности аппроксимации.

Выбор вида аппроксимирующей функции.

Разработано большое количество методов определения, отличающихся друг от друга структурой модели, критериями приближения, особенностью выполнения расчётов. Применим хорошо зарекомендовавший себя метод, согласно которому, передаточная функция модели ищется в виде:

(2)

где: Т₁, T₂, k, t — соответствующие постоянные времени, коэффициент передачи, запаздывание модели объекта.

n — показывает определяющий порядок знаменателя передаточной функции.

Критерием приближения (адекватности) является требование совпадения аппроксимируемой h(t) и аппроксимирующей h_a(t) характеристик в точках t=0, t=¥ и в точке перегиба. Кроме того, в точке перегиба эти характеристики должны иметь одинаковый наклон. Таким образом, критерий приближения имеет следующий вид:

(3)

Для определения производной h’(t) переходной характеристики h(t) в точке, где эта характеристика имеет максимальный наклон, проводится касательная и определяется длина отрезка Т₀ заключённого между точкой этой касательной с горизонтальной осью (абсцисс) и линией нового установившегося значения характеристики, то есть с линией h_уст. Приняв значение: 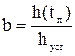, критерий приближённости можно переписать следующим образом:

(4)

Это условие позволяет найти численные значения постоянной времени Т₁, Т₂, величину t_п.а. и запаздывание t = t_п ‑ t_п.а. аппроксимирующей передаточной функции.

Дата добавления: 2015-10-31