Последовательность расчета оптимальных настроек цифровых регуляторов.

Расчёт оптимальных настроек цифровых регуляторов произведем на ЭВМ. Расчёт осуществляется методом расширенных частотных характеристик и проводится в два этапа. На первом этапе производим расчёт и построение в плоскости параметров настроек регулятора линии равной степени колебательности (m=const), на втором этапе определяем в области заданного запаса устойчивости настройки регулятора, обеспечивающие наилучшее качество регулирования. Линия равной степени колебательности m=const строится в плоскости параметров определяемых по формулам: 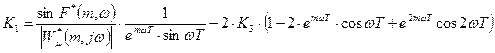(25)

(26)

Процесс расчета оптимальных настроечных параметров будет состоять из следующих этапов:

1. Задаемся значением периода квантования Т. Увеличение периода квантования ведет к ухудшению качества процесса регулирования. Однако, при очень малых Т улучшение качества достигается за счет существенного возрастания затрат на управление. Поэтому не следует выбирать период квантования слишком малым. Для нахождения приемлемого периода квантования можно использовать следующие рекомендации:

Т=0,01Т₉₅¸0,1Т₀, в нашем случае T=(0,0605¸0,375) мин,

где Т₉₅ ─ время достижения регулируемой координаты величины, равной 95% ее установившегося значения при действии на объект ступенчатого возмущения; Т₀─ доминирующая постоянная времени объекта.

2. Задаемся значением параметра k₃ = 0 и строим в плоскости параметров k₁, k₂ по уравнениям (25), (26) линию m = m₃. При расчетах промышленных систем регулирования следует выбирать значение степени колебательности m из диапазона 0,221 < m < 0,366, что обеспечит степень затухания наиболее колебательной составляющей переходного процесса в пределах 0,75 < ψ< 0,9. В нашем случае при нахождени настроек примем m=0,221.

3. Примем в качестве оптимальных такие значения настроек ПИ- и ПИД‑регулятора, при которых система обладает запасом устойчивости не ниже заданного (m>m₃) и коэффициент при интегральной составляющей в законе интегрирования имеет максимальную величину (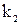 =max). Таким образом, для нахождения оптимальных настроек k₁, k₂, при заданных Т и , достаточно определить точку максимума кривой, равной степени колебательности m=m_з.

4. По определённым оптимальным настройкам k₁, k₂ задаёмся значением параметра из диапазона: 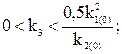строим в плоскости параметров новую линию m=m₃ и определяем новые значения оптимальных настроечных параметров. Такой порядок нахождения значения коэффициента k₃ связан с тем, что качество регулирования улучшается при увеличении k₃ лишь до некоторого его критического значения. Дальнейшее увеличение k₃ приводит к ухудшению качества регулирования.

5. Задаваясь рядом других значений периода квантования Т из диапазона Т=0,01Т₉₅¸0,1Т₀, определяем для них оптимальные настройки. Вычисление расширенной комплексной частотной характеристики эквивалентного объекта произведён по формуле:

(27)

Дата добавления: 2015-10-31