
Читайте также:
|
В цьому випадку відповідний вектор відносних оцінок  .
.
Варіювання коефіцієнта ЦФ базисної змінної впливає на відносні оцінки усіх небазисних змінних. Нехай змінюється коефіцієнт ЦФ  -ї базисної змінної
-ї базисної змінної 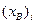 . В цьому випадку вектор коефіцієнтів ЦФ зміниться таким чином:
. В цьому випадку вектор коефіцієнтів ЦФ зміниться таким чином:
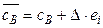 .
.
Тоді вектор відносних оцінок стане рівним

де  –
–  -й рядок матриці
-й рядок матриці 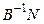 (коефіцієнти
(коефіцієнти  -го рядка симплекс-таблиці, що відповідають небазисним змінним).
-го рядка симплекс-таблиці, що відповідають небазисним змінним).
Відносна оцінка  -ої небазисної змінної
-ої небазисної змінної
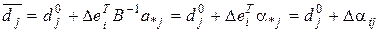 ,
,
де 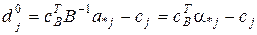 - відносна оцінка
- відносна оцінка  -ої небазисної змінної в поточному оптимальному розв’язку
-ої небазисної змінної в поточному оптимальному розв’язку  .
.
Для того, щоб розв’язок залишався оптимальним, повинна виконуватися умова
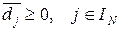 ,
,
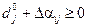
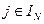 ,
,
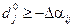 ,
, 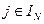 .
.
Розділимо  -ту нерівність на
-ту нерівність на  :
:
якщо 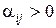 , то відповідна нерівність прийме вигляд
, то відповідна нерівність прийме вигляд  ,
,
якщо  , то відповідна нерівність прийме вигляд
, то відповідна нерівність прийме вигляд 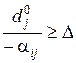 .
.
Отже, для базисної змінної діапазон стійкості, в якому може змінюватися коефіцієнт ЦФ 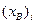 , залишаючи поточний розв’язок оптимальним, задається виразом:
, залишаючи поточний розв’язок оптимальним, задається виразом:
– відносний діапазон:
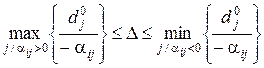
| (6) |
(якщо відсутні 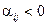 чи
чи 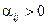 , то
, то  і
і 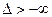 відповідно),
відповідно),
– абсолютний діапазон:  ,
,
Приклад 1
Нехай маємо ЗЛП.
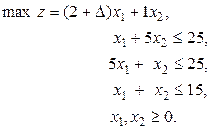
Розв’яжемо задачу за умови  .
.
| БЗ | 
| 
| 
| 
| 
| Розв’язок |
| z | -2- 
| -1 | ||||

| ||||||

| ||||||

|
| БЗ | 
| 
| 
| 
| 
| Розв’язок |
| z | 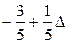
| 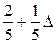
| 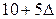
| |||

| 
| 
| ||||

| 
| 
| ||||

| 
| 
|
| БЗ | 
| 
| 
| 
| 
| Розв’язок |
| z | 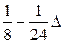
| 
| 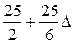
| |||

| 
| 
| 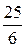
| |||

| 
| 
| 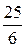
| |||

| 
| 
| 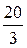
|
Нехай  приймає значення, відмінне від 0. Розв’язок
приймає значення, відмінне від 0. Розв’язок  =
= 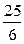 ,
, 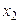 =
= 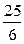 залишиться оптимальним за умови
залишиться оптимальним за умови 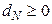 , тобто
, тобто
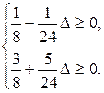
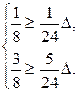
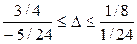 ,
,
 .
.
Отже, отримали той же результат, який дає співвідношення (6).
Приклад 2
Нехай для деякої ЗЛП отримали такий оптимальний розв’язок (перетворену задачу):

Якщо коефіцієнт ЦФ базисної змінної  стане рівним
стане рівним 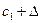 , то відносні оцінки небазисних змінних зміняться таким чином
, то відносні оцінки небазисних змінних зміняться таким чином
 ,
, 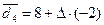 ,
, 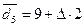 .
.
Відносний діапазон зміни:
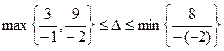 ,
,
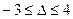 .
.
Абсолютний діапазон зміни: 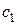 -3 £
-3 £ 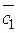 £
£ 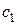 +4.
+4.
9.2.2.2 Задача на мінімум
В цьому випадку в оптимальному розв’язку вектор відносних оцінок
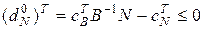 .
.
Для того, щоб розв’язок залишався оптимальним повинна виконуватися умова
 ,
,
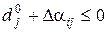
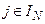 ,
,
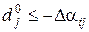 ,
, 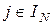 .
.
Розділимо  -ту нерівність на
-ту нерівність на 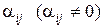 :
:
якщо 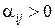 , то відповідна нерівність прийме вигляд
, то відповідна нерівність прийме вигляд 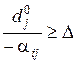 ,
,
якщо  , то відповідна нерівність прийме вигляд
, то відповідна нерівність прийме вигляд 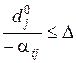 .
.
Тоді в задачі на мінімум для базисної змінної діапазон стійкості задається виразом:
– відносний діапазон: 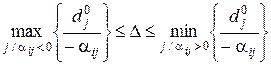
(якщо відсутні  чи
чи 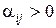 , то
, то 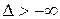 і
і  відповідно),
відповідно),
– абсолютний діапазон: 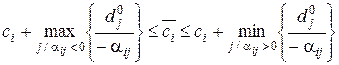 .
.
Висновки
1 Існує діапазон зміни коефіцієнтів ЦФ як базисних, так і небазисних змінних, в яких поточний оптимальний розв’язок залишається оптимальним.
– для небазисних змінних існує тільки нижня або верхня межа;
– для базисних - зазвичай існують і нижня і верхня межі.
2 Зміна коефіцієнта ЦФ базисної змінної завжди приводить до зміни значення ЦФ (оскільки 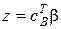 , а
, а  - змінюється).
- змінюється).
3 Ефект від зміни коефіцієнтів ЦФ може розглядатися з двох позицій:
– з погляду збуту нас цікавлять рівноважні ціни;
– з погляду виробництва нас цікавить діапазон зміни коефіцієнта ЦФ, в межах якого поточний план виробництва залишається оптимальним.
9.3 Аналіз зміни коефіцієнтів матриці обмежень
Коефіцієнти  , як правило, відомі з більшою достовірністю, ніж компоненти вектора ЦФ
, як правило, відомі з більшою достовірністю, ніж компоненти вектора ЦФ 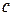 або вектора обмежень
або вектора обмежень 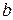 , оскільки зазвичай вони задаються особливостями технологічного процесу і не залежать так сильно від ринкових змін, як ціни або об'єми ресурсів.
, оскільки зазвичай вони задаються особливостями технологічного процесу і не залежать так сильно від ринкових змін, як ціни або об'єми ресурсів.
Розглядатимемо зміни коефіцієнтів, відповідних тільки небазисним змінним, оскільки зміна значень коефіцієнтів  при базисних змінних приводить до зміни базисної матриці
при базисних змінних приводить до зміни базисної матриці 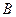 , і проаналізувати це дуже складно.
, і проаналізувати це дуже складно.
Нехай 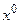 – оптимальний розв’язок,
– оптимальний розв’язок, 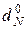 – відповідний вектор відносних оцінок небазисних змінних,
– відповідний вектор відносних оцінок небазисних змінних, 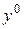 – цінності ресурсів,
– цінності ресурсів,  – небазисна змінна
– небазисна змінна
Спочатку розглянемо випадок, коли змінюється тільки одна компонента одного з небазисних векторів, а потім – випадок одночасної зміни усіх компонент небазисного вектора.
9.3.1 Аналіз зміни одного елемента матриці 
Якщо 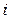 -ий компонент вектора
-ий компонент вектора 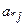 зміниться на величину D, то це вплине тільки на відносну оцінку
зміниться на величину D, то це вплине тільки на відносну оцінку 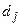 цієї змінної. Нехай
цієї змінної. Нехай  , тоді
, тоді
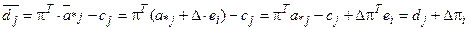 ,
,
де 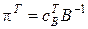 - вектор оцінок обмежень.
- вектор оцінок обмежень.
В точці оптимуму маємо: 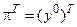 . Отже
. Отже 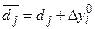 .В задачі на максимум розв’язок залишається оптимальним, якщо
.В задачі на максимум розв’язок залишається оптимальним, якщо 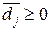 , тобто
, тобто
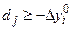
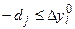 .
.
Тоді діапазон допустимих змін такий:
якщо 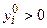 , то
, то 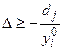 ;
;
якщо 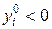 , то
, то 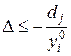 .
.
9.3.2 Умови, при яких неефективний вид діяльності становиться ефективним
Випадок одночасної зміни усіх компонент небазисного вектора  розглянемо на конкретному прикладі.
розглянемо на конкретному прикладі.
Змістовна постановка задачі
Підприємство випускає три види продукції:  ,
,  та
та  . У процесі виробництва використовують три технологічні операції. На рисунку 9.5 показано технологічну схему виробництва продукції.
. У процесі виробництва використовують три технологічні операції. На рисунку 9.5 показано технологічну схему виробництва продукції.
ОШИБКА!!!! В РИСУНКЕ!!!
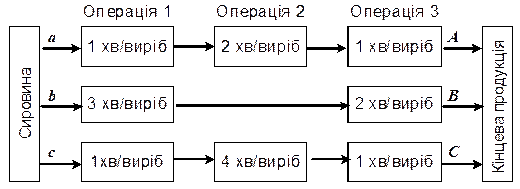
Рисунок 9.5
У прямокутниках вказано тривалість технологічних операцій при виготовленні однієї одиниці продукції кожного виду. Оскільки ці технологічні операції підприємство використовує і для інших виробничих цілей, фонд робочого часу, протягом якого операції 1, 2 і 3 можуть бути використані для виробництва продукції  ,
,  та
та  ., обмежений такими значеннями (за добу): для першої операції – 430 хв, для другої операції – 460 хв, для третьої операції – 420 хв. Ціна продажу одиниці продукції
., обмежений такими значеннями (за добу): для першої операції – 430 хв, для другої операції – 460 хв, для третьої операції – 420 хв. Ціна продажу одиниці продукції  ,
,  та
та  складає 3, 2 і 5 грн відповідно.
складає 3, 2 і 5 грн відповідно.
Визначити найбільш вигідний добовий обсяг виробництва кожного виду продукції.
Математична модель задачі
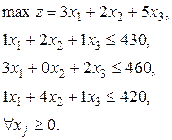
Оптимальний розв’язок задачі
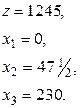
Двоїста задача
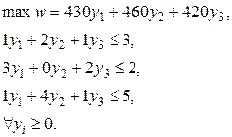
Оптимальний розв’язок двоїстої задачі
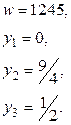
Оптимальний розв’язок передбачає виробництво продукції  та
та  , і вимагає відмови від виробництва продукції
, і вимагає відмови від виробництва продукції  . Це означає, що в поточній економічній ситуації виробництво продукції
. Це означає, що в поточній економічній ситуації виробництво продукції  не рентабельне (навіть якщо
не рентабельне (навіть якщо 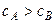 ). Разом з цим ринок продукції вимагає випуску цього виду продукції. Розглянемо як зробити прибутковим виробництво продукції
). Разом з цим ринок продукції вимагає випуску цього виду продукції. Розглянемо як зробити прибутковим виробництво продукції  . Згідно теорії ЛП виробництво продукції
. Згідно теорії ЛП виробництво продукції  буде вигідним тільки тоді, коли
буде вигідним тільки тоді, коли
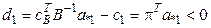
| (7) |
В оптимальному розв’язку 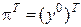 , де
, де 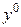 – вектор оптимальних значень двоїстих змінних (цінності ресурсів). Значить (7) можна переписати таким чином:
– вектор оптимальних значень двоїстих змінних (цінності ресурсів). Значить (7) можна переписати таким чином:
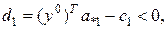
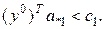
| (8) |
Коли ми розглядали економічну інтерпретацію двоїстої задачі, прийшли до висновку, що в ліва частина відношення (8)– це вартість ресурсів, необхідних для виробництва однієї одиниці продукції відповідного виду. Отже необхідно, або збільшити коефіцієнт 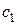 (прибуток від продажу одиниці продукції
(прибуток від продажу одиниці продукції  ) шляхом збільшення ціни продукції, або знизити вартість ресурсів необхідних для виробництва цієї продукції.
) шляхом збільшення ціни продукції, або знизити вартість ресурсів необхідних для виробництва цієї продукції.
Зростання ціни продукції небажане, оскільки це знизить їх конкурентну спроможність на ринку. Більш привабливим є зменшення величини  . Для цього необхідно просто скоротити час виконаних операцій, необхідних для виробництва продукції
. Для цього необхідно просто скоротити час виконаних операцій, необхідних для виробництва продукції  .
.
Нехай 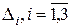 – частка (доля) (
– частка (доля) (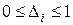 ) скорочення часу операції
) скорочення часу операції 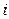 на обробку одиниці продукції
на обробку одиниці продукції  .
.
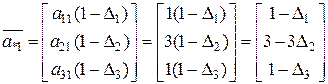 .
.
Визначимо значення 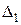 ,
,  ,
, 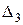 з умови
з умови  ,
,
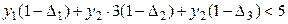
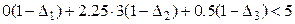
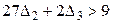
| (9) |
Таким чином, будь-які значення величин 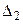 та
та 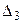 від 0 до 1, що задовольняють нерівності (9), приведуть до прибутковості виробництва продукції
від 0 до 1, що задовольняють нерівності (9), приведуть до прибутковості виробництва продукції  , наприклад:
, наприклад: 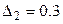 та
та 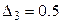 . Відмітимо, що скорочення часу виконання другої операції в 13,5 раз вигідніше (ефективніше) скорочення часу виконання третьої операції.
. Відмітимо, що скорочення часу виконання другої операції в 13,5 раз вигідніше (ефективніше) скорочення часу виконання третьої операції.
9.4 Приклад постоптимального аналізу ЗЛП
Постоптимальний аналіз ЗЛП розглянемо на прикладі задачі визначення оптимального асортименту продукції кондитерського цеху.
9.4.1 Змістовна постановка задачі
Кондитерський цех випускає чотири види виробів: ватрушки, сушки, пиріжки з повидлом, здобні булочки (одиниця випуску — контейнер). У виробництві продукції використовують три види ресурсів: пшеничне борошно, цукор, дріжджі. Добові обсяги використання борошна і цукру обмежені: цукор — 70 мішків, борошно — 80 мішків. Умови постачання й особливості збереження дріжджів визначають обсяг їх використання — не менше 25 кг на день. Витрати вихідних продуктів відповідно до рецептури їх виготовлення наведені у табл. 1.
Таблиця 1
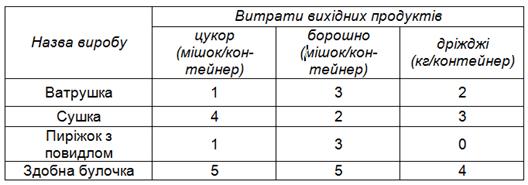
Цех має ряд постійних клієнтів (кафе, кіоски). Відповідно до договорів з ними добові постачання ватрушок, пиріжків з повидлом і здобних булочок складають не менше 10 контейнерів у день. При цьому обсяг випуску сушок повинен дорівнювати сумі обсягу випуску пиріжків і подвоєному обсягу випуску ватрушок. Прибуток за один контейнер ватрушок, сушок, пиріжків з повидлом і здобних булочок складає 15, 10, 8 і 2 од. вартості відповідно.
Знайдіть добові обсяги випуску продукції кожного виду для одержання максимального прибутку.
Дата добавления: 2015-10-31; просмотров: 136 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача на максимум | | | Математична модель |