
Читайте также:
|
Змінні:  – добовий обсяг випуску продукції
– добовий обсяг випуску продукції  -го виду у контейнерах (
-го виду у контейнерах ( — ватрушки, сушки, пиріжки з повидлом і здобні булочки відповідно).
— ватрушки, сушки, пиріжки з повидлом і здобні булочки відповідно).
Цільова функція: сумарний добовий прибуток від реалізації усіх кондитерських виробів
max  .
.
Обмеження
Сумарний добовий обсяг використаного цукру не може перевищувати його максимального добового запасу у 70 мішків:
 .
.
Сумарний добовий обсяг використаного борошна не може перевищувати його максимального добового запасу у 80 мішків:
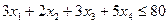 .
.
Сумарний добовий обсяг використання дріжджів не може бути менше ніж 25 кг:
 .
.
Сумарний обсяг випуску ватрушок, пиріжків і здобних булочок не може бути менше 10 контейнерів у день:
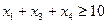 .
.
Співвідношення обсягів випуску ватрушок, сушок і пиріжків у контейнерах (обмеження, що враховують комплектність випуску продукції):
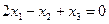 .
.
Усі змінні повинні бути невід’ємні:
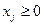 ,
, 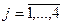 .
.
9.4.3 Розв’язання засобами MICROSOFT EXCEL
Заповнимо лист MICROSOFT EXCEL відповідними даними і введемо формули так, як це показано на рис. 9.6.

Рисунок 9.6
У діалоговому вікні Поиск решения заповнемо всі необхідні поля (комірку цільової функції, напрям оптимізації, діапазон комірок-змінних і використовувані обмеження) (рис. 9.7).
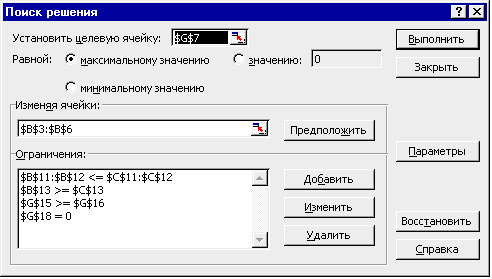
Рисунок 9.7
Результати пошуку розв’язку показано на рис. 9.8.

Рисунок 9.8
Засобами MICROSOFT EXCEL можна провести аналіз на чутливість до зміни параметрів моделі задачі лінійного програмування. Для цього у діалоговому вікні Результаты поиска решения необхідно вибрати Тип отчета: Устойчивость. Після цього MICROSOFT EXCEL створить новий лист — Звіт про стійкість 1.
Звіт за результатами показано на рис. 9.9, звіт про стійкість — рис. 9.10.
Рисунок 
9.9
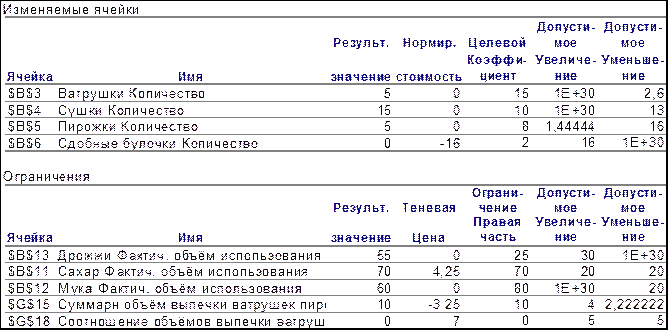 Рисунок 9.10
Рисунок 9.10
9.4.4. Розв’язання задачі симплекс-методом
Зведемо задачу до канонічної форми:

Результати ітерацій розв’язання задачі табличним двоетапним симплекс-методом наведено у табл. 2 — 9. Результати реалізації етапу I представлено у табл. 2 — 7, етапу II — у табл. 8 — 9.
Таблиця 2
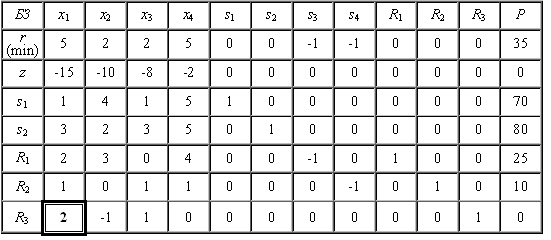
Тут і далі БЗ — базисні змінні, Р — розв’язок.
Таблиця 3

Таблиця 4

Таблиця 5
Таблиця 6

Таблиця 7

Етап І завершено, оскільки  і усі штучні змінні є небазисними, тобто отримали оптимальний розв’язок початкової задачі. Переходимо до етапу ІІ: видаляємо
і усі штучні змінні є небазисними, тобто отримали оптимальний розв’язок початкової задачі. Переходимо до етапу ІІ: видаляємо  -рядок, але стовпці, що відповідають штучним змінним, із таблиці вилучати не будемо — надалі для проведення постоптимального аналізу моделі нам знадобляться ці стовпці результуючої оптимальної симплекс-таблиці. У таблицях наступних ітерацій коефіцієнти
-рядок, але стовпці, що відповідають штучним змінним, із таблиці вилучати не будемо — надалі для проведення постоптимального аналізу моделі нам знадобляться ці стовпці результуючої оптимальної симплекс-таблиці. У таблицях наступних ітерацій коефіцієнти  -рядка для штучних змінних не обчислюємо (оскільки у разі використання двоетапного методу на другому етапі ці коефіцієнти не мають змісту).
-рядка для штучних змінних не обчислюємо (оскільки у разі використання двоетапного методу на другому етапі ці коефіцієнти не мають змісту).
Таблиця 8

Таблиця 9

Таблиця 10

Отже:  ,
,  ,
,  ,
,  ,
,  .
.
9.4.5 Визначення цінностей ресурсів
Одне з основних положень теорії двоїстості: цінність ресурсу збігається зі значенням відповідної двоїстої змінної.
9.4.5.1 Визначення цінностей ресурсів способом 1
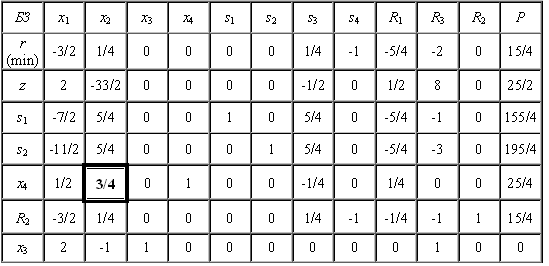
Початкова симплекс-таблиця прямої задачі зображена у таблиці 11. В ній виділені вектор-стовпці, які складали початкову базисну матрицю.
Таблиця 11

В таблиці 12, що відповідає оптимальному розв’язку задачі, відповідні стовпці містять поточну обернену матрицю.
Таблиця 12

Оптимальний розв’язок двоїстої задачі (цінності ресурсів) знаходимо із співвідношення

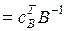 .
.
де  - матриця, обернена до базисної, яка відповідає оптимальному ДБР,
- матриця, обернена до базисної, яка відповідає оптимальному ДБР,
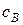 – підвектор коефіцієнтів цільової функції, що відповідають базисним змінним оптимального розв’язку.
– підвектор коефіцієнтів цільової функції, що відповідають базисним змінним оптимального розв’язку.
З оптимальної симплекс-таблиці виділяємо обернену базисну матрицю, що відповідає оптимуму:
 .
.
З урахуванням того, що  = (15, 0, 10, 0, 8), маємо
= (15, 0, 10, 0, 8), маємо
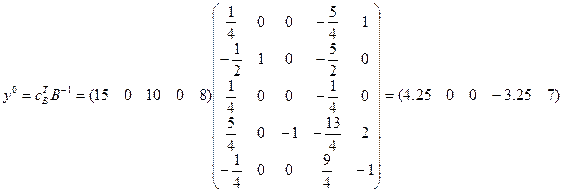 .
.
Відзначимо, що отримані аналітичним шляхом значення цінності ресурсів повністю збігаються з результатами MICROSOFT EXCEL (див. рис. 9.10 — стовпець Тіньова ціна).
9.4.5.2 Визначення цінностей ресурсів способом 2
Побудуємо задачу, двоїсту до розглянутої.
Пряма задача:

Двоїста задача має такий вигляд:

В оптимальній таблиці прямої задачі (див. табл. 10) базисними є змінні  ,
,  ,
,  ,
,  ,
,  . Згідно з співвідношеннями доповнюючої нежорсткості відповідні цим змінним обмеження-нерівності двоїстої задачі в точці оптимуму виконуються як рівності. Таким чином ми одержимо систему лінійних рівнянь, розв’язок якої і дасть нам оптимальні значення двоїстих змінних:
. Згідно з співвідношеннями доповнюючої нежорсткості відповідні цим змінним обмеження-нерівності двоїстої задачі в точці оптимуму виконуються як рівності. Таким чином ми одержимо систему лінійних рівнянь, розв’язок якої і дасть нам оптимальні значення двоїстих змінних:





| базисні | 
| 
| 
| 
|
Розв'язок отриманої системи лінійних рівнянь:

Основна теорема двоїстості: якщо пряма і двоїста задача мають розв’язки, то їх значення співпадають. Переконаємося в цьому:
 Згідно з теорією двоїстості двоїста змінна
Згідно з теорією двоїстості двоїста змінна  (
( ) визначає цінність
) визначає цінність 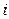 -го ресурсу (оцінку ресурсу, shadow price, тіньову ціну) – значення, на яке зміниться цільова функція у разі збільшення на одиницю рівня запасу відповідного ресурсу (відносну цінність одиниці додаткового ресурсу).
-го ресурсу (оцінку ресурсу, shadow price, тіньову ціну) – значення, на яке зміниться цільова функція у разі збільшення на одиницю рівня запасу відповідного ресурсу (відносну цінність одиниці додаткового ресурсу).
9.4.6. Діапазони стійкості
Визначимо допустимі діапазони, в яких можуть змінюватись рівні запасів ресурсів і цін продукції. При цьому отриманий розв’язок повинен залишатись оптимальним.
9.4.6.1. Зміна компонентів вектора обмежень
Недефіцитні ресурси
У нашій задачі змінна  (базисна, дорівнює 20), отже, другий ресурс недефіцитний. Відповідне обмеження має знак "£", значить діапазон зміни правої частини (
(базисна, дорівнює 20), отже, другий ресурс недефіцитний. Відповідне обмеження має знак "£", значить діапазон зміни правої частини ( ) другого обмеження такий:
) другого обмеження такий:
 ;
;
 ;
;
 ;
;
 .
.
Змінна  (базисна, дорівнює 30), отже, третій ресурс недефіцитний. Відповідне обмеження має знак "³", тоді маємо такий діапазон зміни правої частини (
(базисна, дорівнює 30), отже, третій ресурс недефіцитний. Відповідне обмеження має знак "³", тоді маємо такий діапазон зміни правої частини ( ) третього обмеження:
) третього обмеження:
 ;
;
 ;
;
 ;
;
 .
.
Фрагмент звіту про стійкість показано на рис. 9.11. З нього видно, що вище отримані результати збігаються з результатами MICROSOFT EXCEL.
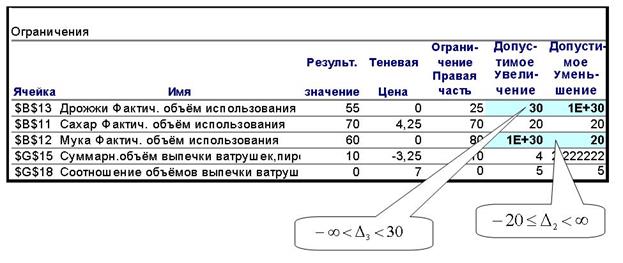
Рисунок 9.11
Дефіцитні ресурси
У нашій задачі змінна  — небазисна, отже, перший ресурс — дефіцитний. Вихідне обмеження має знак "£". У цьому випадку допустимий діапазон змін
— небазисна, отже, перший ресурс — дефіцитний. Вихідне обмеження має знак "£". У цьому випадку допустимий діапазон змін  визначається формулою:
визначається формулою:
 .
.
У оптимальній симплекс-таблиці (рис. 9.12) виділено стовпець  , що відповідає небазисній змінній
, що відповідає небазисній змінній  . Тоді допустимий діапазон змін
. Тоді допустимий діапазон змін  такий:
такий:

 ;
;
 .
.

Рисунок 9.12
Отримані результати співпали з результатами MICROSOFT EXCEL (рис. 9.13 — рядок Сахар Фактич. объём использования, стовпці " Допустимое Увеличение " і " Допустимое Уменьшение ").
Абсолютний діапазон зміни рівня запасу ресурсу такий:
 ,
,
 .
.

Рисунок 9.13
У нашій задачі змінна 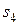 — небазисна, отже, четвертий ресурс — дефіцитний. Вихідне обмеження має знак "³", тоді діапазон зміни
— небазисна, отже, четвертий ресурс — дефіцитний. Вихідне обмеження має знак "³", тоді діапазон зміни  такий
такий


(знаменники дробів узято зі стовпчика  оптимальної симплекс-таблиці, див. рис. 9.12):
оптимальної симплекс-таблиці, див. рис. 9.12):

Маємо збіг із результатами MICROSOFT EXCEL (див. рис. 9.13).
Абсолютний діапазон зміни правої частини обмеження:
 , або
, або 
Проаналізуємо наслідки зміни правої частини останнього обмеження моделі (співвідношення обсягів випуску ватрушок, сушок і пиріжків):  .
.
Обмеження такого роду звичайно є обмеженнями на комплектність випуску продукції. У цьому випадку права частина обмеження, по суті, не може бути відмінною від нуля. Якщо допустити можливість зміни значення правої частини, то у разі аналізу цього ресурсу питання можна було б поставити так: на яку величину сума подвоєного обсягу випуску ватрушок і та обсягу випуску пиріжків може перевищувати (або бути менше) обсяг випуску сушок. У такому контексті обмеження перестає бути обмеженням — вимогою комплектності продукції.
У початковому допустимому базисному розв'язку це обмеження містило штучну базисну змінну  (цю змінну можна розглядати як невід’ємну залишкову, тому для визначення діапазону змін
(цю змінну можна розглядати як невід’ємну залишкову, тому для визначення діапазону змін  слід використовувати співвідношення (4)).
слід використовувати співвідношення (4)).
 ;
;

 або
або 
4.6.2. Зміна коефіцієнтів цільової функції
Небазисні змінні
У нашій задачі (див. оптимальну симплекс-таблицю на рис. 9.14), змінна  є небазисною, тому для неї
є небазисною, тому для неї


що збігається з результатами MICROSOFT EXCEL (відповідний фрагмент звіту про стійкість зображено на рис. 9.15). Тоді із врахуванням початкових значень діапазон зміни коефіцієнта цільової функції при даній змінній
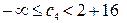 або
або  .
.

Рисунок 9.14
 Рисунок 9.15
Рисунок 9.15
Базисні змінні
Наша задача – задача на максимум, тоді для базисної змінної діапазон стійкості, у якому може змінюватися коефіцієнт  , залишаючи поточний розв'язок оптимальним, задається виразом:
, залишаючи поточний розв'язок оптимальним, задається виразом:
 , де
, де
 .
.
Змінна  — базисна (дані узято з оптимальної симплекс-таблиці, див. рис. 4.9). Отже
— базисна (дані узято з оптимальної симплекс-таблиці, див. рис. 4.9). Отже


Із урахуванням початкових значень абсолютний діапазон зміни коефіцієнта цільової функції даної змінної:

Змінна  — базисна (див. рис. 9.14), тоді
— базисна (див. рис. 9.14), тоді

 .
.
Абсолютний діапазон зміни коефіцієнта цільової функції для цієї змінної:


Змінна  — базисна:
— базисна:

Абсолютний діапазон зміни коефіцієнта цільової функції для цієї змінної:

Всі результати збігаються з результатами MICROSOFT EXCEL EXCEL (див. рис. 9.15).
Для залишкових і надлишкових змінних (у нас —  і
і  ) такий аналіз не проводять.
) такий аналіз не проводять.
9.4.6.3. Інтерпретація результатів розв’язання і постоптимального аналізу задачі
Оптимальний розв’язок задачі
При вихідних даних оптимальні обсяги випуску продукції такі:
– ватрушки — 5 контейнерів;
– сушки —15 контейнерів;
– пиріжки з повидлом — 5 контейнерів;
– здобні булочки — 0 контейнерів.
При цьому прибуток становитиме 265 од. вартості.
Діапазони зміни рівня запасів ресурсів.
Відносні діапазони зміни рівнів запасів ресурсів (на скільки можуть зменшитися або збільшитися рівні запасів, не впливаючи на розв’язок) ( ):
):
– добові запаси цукру 
– добові запаси борошна 
– добові запаси дріжджів 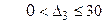 (запаси дріжджів не можуть бути від’ємними);
(запаси дріжджів не можуть бути від’ємними);
– обсяги обов'язкових постачань 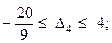
– перевищення суми обсягу випуску пиріжків і подвоєного обсягу випуску ватрушок над обсягом випуску сушок  .
.
Абсолютні діапазони зміни рівнів запасів ресурсів (до яких меж можна зменшувати або збільшувати рівні запасів  ):
):
– добові запаси цукру 
– добові запаси борошна 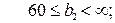
– добові запаси дріжджів 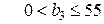 (запаси дріжджів не можуть бути від’ємними);
(запаси дріжджів не можуть бути від’ємними);
– обсяги обов'язкових постачань 
– перевищення суми обсягу випуску пиріжків і подвоєного обсягу випуску ватрушок над обсягом випуску сушок 
Цінність ресурсів
Статус і цінність ресурсів наведені в табл. 13.
Таблиця 13

У разі зміни рівнів запасів ресурсів у знайдених діапазонах, маємо:
– кожний додатковий мішок цукру дозволить збільшити сумарний прибуток на 4,25 од. вартості (відповідно, нестача одного мішка цукру приведе до зменшення сумарного прибутку пекарні на 4,25 од. вартості);
– зміна рівнів запасів борошна і дріжджів не приведуть до зміни сумарного прибутку;
– кожний додатковий контейнер обов'язкових кондитерських виробів відповідно до договорів із постійними клієнтами зменшить сумарний прибуток на 3,25 од. вартості (зменшення на один контейнер обсягу обов'язкових постачань приведе до збільшення сумарного прибутку на 3,25 од. вартості);
– збільшення (зменшення) різниці обсягів випуску ватрушок, пиріжків і сушок  на один контейнер приведе до збільшення (зменшення) сумарного прибутку на 7 од. вартості.
на один контейнер приведе до збільшення (зменшення) сумарного прибутку на 7 од. вартості.
Діапазони зміни цін продукції
Допустимі відносні діапазони зміни цін продукції, за яких оптимальний розв’язок не зміниться:
– ватрушки 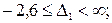
– сушки 
– пиріжки 
– булочки 
Допустимі абсолютні діапазони зміни цін продукції, за яких оптимальний розв’язок не зміниться:
– ватрушки – 
– сушки 
– пиріжки 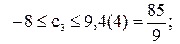
– булочки 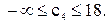

Дата добавления: 2015-10-31; просмотров: 299 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача на максимум | | | Прочие условия |