
Читайте также:
|
Приклад
Розглянемо обмеження–нерівність  .
.
Приведемо його до канонічної форми  .
.
Якщо в оптимальному розв’язку  , то вихідні змінні задачі (
, то вихідні змінні задачі ( ) задовольнятимуть нерівності
) задовольнятимуть нерівності  , а також будь-який іншій нерівності такого ж вигляду, але із значенням правої частини, більшим ніж 80. Отже
, а також будь-який іншій нерівності такого ж вигляду, але із значенням правої частини, більшим ніж 80. Отже  , або
, або  .
.
9.1.2 Дефіцитний ресурс
Якщо додаткова змінна  небазисна, то аналізоване обмеження є зв’язуючим (активним в точці оптимуму), а ресурс — дефіцитним.
небазисна, то аналізоване обмеження є зв’язуючим (активним в точці оптимуму), а ресурс — дефіцитним.
При зміні відповідної компоненти вектора  змінюється і вектор
змінюється і вектор  і значення ЦФ
і значення ЦФ  . При цьому існує діапазон змін
. При цьому існує діапазон змін  , при яких
, при яких  , тобто, значення базисних змінних змінюються, але не змінюється базис оптимального розв’язку. В цьому випадку питання стоїть так: знайти такий діапазон зміни компонента
, тобто, значення базисних змінних змінюються, але не змінюється базис оптимального розв’язку. В цьому випадку питання стоїть так: знайти такий діапазон зміни компонента  , при якому базис оптимального розв’язку не зміниться (тобто розв'язок залишається оптимальним в тому сенсі, що базис його не змінюється).
, при якому базис оптимального розв’язку не зміниться (тобто розв'язок залишається оптимальним в тому сенсі, що базис його не змінюється).
9.1.2.1 Обмеження виду “£”
Розглянемо обмеження виду “£”:

| (1) |
де  — залишкова змінна.
— залишкова змінна.
Нехай тепер права частина обмеження зміниться на 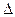 , тобто прийме значення
, тобто прийме значення  , тоді рівняння (1) можна переписати у вигляді
, тоді рівняння (1) можна переписати у вигляді
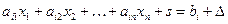 ,
,
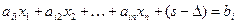
| (2) |
отже ( ) замінює
) замінює  .
.
Оскільки в оптимальному розв’язку змінна  небазисна (=0), то компоненти вектора
небазисна (=0), то компоненти вектора  при зміні
при зміні  змінюються згідно рівняння:
змінюються згідно рівняння:
 ,
,
 ,
,
 ,
,
де  — стовпець оптимальної симплекс-таблиці, відповідний змінній
— стовпець оптимальної симплекс-таблиці, відповідний змінній  :
:
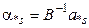 .
.
Оскільки всі компоненти вектора 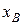 мають бути ³ 0, то отримаємо:
мають бути ³ 0, то отримаємо:
 ,
,

| (3) |
Співвідношення (3) – це система з  нерівностей:
нерівностей:
 ,
,  .
.
Розділимо  -ту нерівність на
-ту нерівність на  :
:
якщо  , то відповідна нерівність прийме вигляд
, то відповідна нерівність прийме вигляд 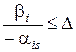 ;
;
якщо  , то відповідна нерівність прийме вигляд
, то відповідна нерівність прийме вигляд  .
.
Таким чином, діапазон змін:
 (від’ємні) (додатні)
(від’ємні) (додатні)
| (4) |
Якщо немає жодного  , то
, то  .
.
Якщо немає жодного  то
то  .
.
Вираз (4) дає відносний діапазон змін, абсолютний діапазон зміни рівня запасу дефіцитного ресурсу такий:
 ,
,
На рисунку 9.3 проілюстровано діапазон можливих змін коефіцієнта  для зв’язуючого обмеження виду “£”.
для зв’язуючого обмеження виду “£”.

Рисунок 9.3
Приклад
Нехай маємо ЗЛП.
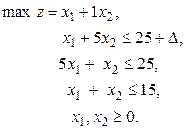
Розв’яжемо задачу за умови  .
.
| БЗ | 
| 
| 
| 
| 
| Розв’язок |
| z | -2 | -1 | ||||

| 25+ 
| |||||

| ||||||

|
| БЗ | 
| 
| 
| 
| 
| Розв’язок |
| z | 
| 
| ||||

| 
| 
| 20+ 
| |||

| 
| 
| ||||

| 
| 
|
| БЗ | 
| 
| 
| 
| 
| Розв’язок |
| z | 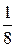
| 
| 
| |||

| 
| 
| 
| |||

| 
| 
| 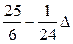
| |||

| 
| 
| 
|
Нехай  приймає значення, відмінне від 0. Отриманий розв’язок залишиться допустимим і оптимальним за умови
приймає значення, відмінне від 0. Отриманий розв’язок залишиться допустимим і оптимальним за умови  , тобто
, тобто
 ,
,
Або

Розв’язками системи нерівностей є:  .
.
Отже, отримали той же результат, який дає співвідношення (4).
9.1.2.2. Обмеження виду “³”
Розглянемо обмеження виду “³”:

| (5) |
при приведенні до канонічної форми вводиться надлишкова змінна:
 .
.
Нехай запас ресурсу змінився на величину  :
:
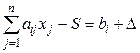 ,
,
 .
.
Оскільки в оптимальному розв’язку змінна  небазисна (=0), то компоненти вектора
небазисна (=0), то компоненти вектора  при зміні
при зміні  змінюються згідно рівняння:
змінюються згідно рівняння:
 ,
,
 ,
,
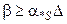 .
.
Отримали систему з  нерівностей, перепишемо її так:
нерівностей, перепишемо її так:
 ,
, 
Розділимо  -ту нерівність на
-ту нерівність на 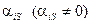 :
:
якщо  , то відповідна нерівність прийме вигляд
, то відповідна нерівність прийме вигляд  або
або 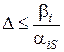 ,
,
якщо  , то відповідна нерівність прийме вигляд
, то відповідна нерівність прийме вигляд 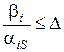 .
.
Таким чином, діапазон змін величини  :
:
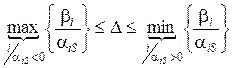 .
.
Якщо немає жодного  , то
, то  ,
,
якщо немає жодного  , то
, то 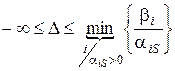 .
.
Абсолютний діапазон зміни рівня запасу дефіцитного ресурсу такий:
 .
.
На рисунку 9.4 проілюстровано діапазон можливих змін коефіцієнта  для обмеження виду “³”.
для обмеження виду “³”.
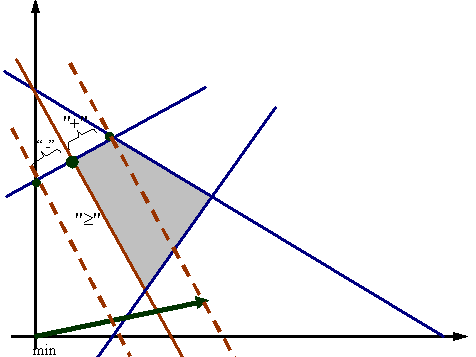
Рисунок 9.4
Цей аналіз можна провести і іншим шляхом, розглядаючи зміну компонентів вектора обмежень у вигляді

де  — одиничний вектор, відповідний аналізованому обмеженню. Тоді нове значення
— одиничний вектор, відповідний аналізованому обмеженню. Тоді нове значення  :
:
 ,
,
Обмеження виду «£»
Стовпець перетвореної задачі, що відповідає залишковій змінній  :
:  оскільки стовпець матриці обмежень, відповідний залишковій змінній
оскільки стовпець матриці обмежень, відповідний залишковій змінній  — одиничний.
— одиничний.
Обмеження виду «³»
Стовпець перетвореної задачі, що відповідає надлишковій змінній  :
:  , оскільки стовпець матриці обмежень, відповідний надлишковій змінній
, оскільки стовпець матриці обмежень, відповідний надлишковій змінній  такий:
такий:
 .
.
Таким чином, маємо:
– для обмежень «£»:  ,
,  ;
;
– для обмежень «³»: 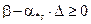 ,
,  .
.
Що збігається з отриманим раніше.
9.2 Аналіз зміни коефіцієнтів ЦФ
9.2.1 Небазисна змінна
Зміна коефіцієнта ЦФ небазисної змінної впливає на відносну оцінку тільки цієї змінної.
Задача на максимум
Нехай  – оптимальний розв’язок, значить відповідний вектор відносних оцінок небазисних змінних
– оптимальний розв’язок, значить відповідний вектор відносних оцінок небазисних змінних
 .
.
Відносна оцінка небазисної змінної  :
:
 ,
,
величина  не входить у вираз компонентів вектора
не входить у вираз компонентів вектора  , які відповідають іншим змінним.
, які відповідають іншим змінним.
Нехай коефіцієнт ЦФ при небазисній змінній  прийняв значення
прийняв значення
 ,
,
тоді її нова відносна оцінка буде такою:

Розв’язок залишиться оптимальним, якщо  або
або  . Отже, для небазисної змінної
. Отже, для небазисної змінної 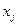 діапазон стійкості в якому може змінюватися її коефіцієнт ЦФ:
діапазон стійкості в якому може змінюватися її коефіцієнт ЦФ:
– відносний діапазон:  ,
,
– абсолютний діапазон:  ,
,
де  - відносна оцінка змінної
- відносна оцінка змінної 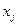 в оптимальному розв’язку.
в оптимальному розв’язку.
Якщо  (
( ), то
), то  стане одним з альтернативних оптимумів.
стане одним з альтернативних оптимумів.
9.2.1.2 Задача на мінімум
Нехай  – оптимальний розв’язок, значить відповідний вектор відносних оцінок небазисних змінних
– оптимальний розв’язок, значить відповідний вектор відносних оцінок небазисних змінних
 .
.
Нехай коефіцієнт ЦФ при небазисній змінній  прийняв значення
прийняв значення
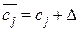
тоді її нова відносна оцінка буде такою:

Розв’язок залишиться оптимальним, якщо 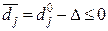 або
або  . Отже, для небазисної змінної
. Отже, для небазисної змінної 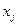 діапазон стійкості в якому може змінюватися її коефіцієнт ЦФ:
діапазон стійкості в якому може змінюватися її коефіцієнт ЦФ:
– відносний діапазон:  ,
,
– абсолютний діапазон:  ,
,
де  - відносна оцінка змінної
- відносна оцінка змінної  в оптимальному розв’язку.
в оптимальному розв’язку.
9.2.1.3 Рівноважна ціна
Нехай маємо деякий виробничий процес і нехай змінна 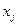 - кількість виробництва
- кількість виробництва  -го продукту, який може бути проданий за ціною
-го продукту, який може бути проданий за ціною  од.варт./од.прод. І нехай в оптимальному розв’язку ця змінна небазисна (випуск цього продукту – не вигідний, тому він не виробляється) і її відносна оцінка дорівнює 2 од.варт./од.прод. Таким чином, якщо ціна зросте до
од.варт./од.прод. І нехай в оптимальному розв’язку ця змінна небазисна (випуск цього продукту – не вигідний, тому він не виробляється) і її відносна оцінка дорівнює 2 од.варт./од.прод. Таким чином, якщо ціна зросте до 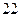 од.варт./од.прод., відносна оцінка стане рівною нулю, і подальше збільшення ціни приведе до від’ємної відносної оцінки, тобто поточний розв’язок перестане бути оптимальним. В цьому випадку стане вигідним виготовляти продукт, представлений змінною
од.варт./од.прод., відносна оцінка стане рівною нулю, і подальше збільшення ціни приведе до від’ємної відносної оцінки, тобто поточний розв’язок перестане бути оптимальним. В цьому випадку стане вигідним виготовляти продукт, представлений змінною 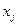 . Отже, 22 од.варт./од.прод.- це рівноважна ціна для
. Отже, 22 од.варт./од.прод.- це рівноважна ціна для 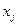 :
:
– при будь-якій нижчій ціні оптимальний розв’язок полягатиме в тому, щоб зовсім не виробляти цей продукт
– при вищій ціні вигідно ввести 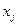 в базис.
в базис.
Продовжимо аналіз. Нехай в деякій ЗЛП ( в оптимальному розв’язку
в оптимальному розв’язку
 ,
,  ,
,  – не базисна,
– не базисна,  ,
,  ,
,  .
.
Таким чином, при ціні 22 ед од.варт./од.прод. і більше стає вигідним виготовляти 4–й продукт і при цьому на кожну виготовлену одиницю 4–го продукту змінні  і
і  зменшуються на 1 і 2 відповідно, а
зменшуються на 1 і 2 відповідно, а  - збільшується на 3.
- збільшується на 3.
Знайдемо: 
 .
.
Якщо ми виготовимо п'ять одиниць продукту 4, то змінна  обернеться в нуль, і подальше збільшення
обернеться в нуль, і подальше збільшення  вимагатиме зміни базису. Відмітимо, що ми виконали ітерацію, не вирішуючи задачу заново. Для продовження аналізу нам потрібно буде лише виконати операцію заміщення, що відповідає зміні базису.
вимагатиме зміни базису. Відмітимо, що ми виконали ітерацію, не вирішуючи задачу заново. Для продовження аналізу нам потрібно буде лише виконати операцію заміщення, що відповідає зміні базису.
9.2.2 Базисна змінна
Нехай  - оптимальний розв’язок ЗЛП.
- оптимальний розв’язок ЗЛП.
Дата добавления: 2015-10-31; просмотров: 113 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| The Moving Finger | | | Задача на максимум |