
|
Читайте также: |
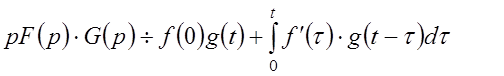 (15)
(15)
Кроме того, имеют место следующие предельные соотношения:
1) 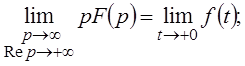
2)  если существует предел
если существует предел 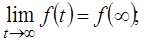
3) 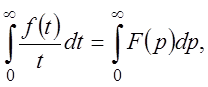 если сходится несобственный интеграл
если сходится несобственный интеграл 
Таблица оригиналов и их изображений
| № | Оригинал | Изображение |
| h (t) | 
| |
| eat | 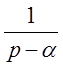
| |
| tn | 
| |
| sinbt | 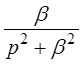
| |
| cosbt | 
| |
| shbt | 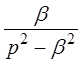
| |
| chbt | 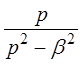
| |
| tneat | 
| |
| eatsinbt | 
| |
| eatcosbt | 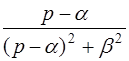
| |
| t×sinbt | 
| |
| t×cosbt | 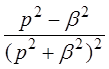
|
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
1. Преобразование Лапласа. Функция-оригинал. Существование и аналитичность преобразования Лапласа.
2. Свойства преобразования Лапласа (линейности, подобия, смещения, запаздывания).
3. Дифференцирование оригинала и изображения.
4. Интегрирование оригинала и изображения.
5. Понятие свертки. Изображение свертки. Интеграл Дюамеля.
6. Методы отыскания оригинала по изображению.
7. Решение линейных дифференциальных уравнений и систем дифференциальных уравнений операционным методом.
ЗАДАНИЯ
Задание1. Пользуясь определением, найти изображения следующих функций:
| 1.1. t | 1.2. sin t | 1.3. cos t |
| 1.4. ch t | 1.5. et | 1.6. 2t |
| 1.7. sin 2t | 1.8. cos 2t | 1.9. sh 2t |
| 1.10. 3t | 1.11. 1 - 2t | 1.12. sin 3t |
| 1.13. t - sin t | 1.14. tet | 1.15. t - et |
| 1.16. sin2t | 1.17. tsh t | 1.18. cos2t |
| 1.19. sin 3t | 1.20. cos 3t | 1.21. sh 3t |
| 1.22. 5t | 1.23. te-2t | 1.24. t sin t |
| 1.25. sh t | 1.26. ch 2t | 1.27. e-5t |
| 1.28. t2 | 1.29. cos 3t | 1.30. tch t |
| 1.31 2t - e2t | 1.32. t cos t | 1.33 3 -5t |
| 1.34. t - cos t | 1.35. 5 - et | 1.36. 3t - 3t |
| 1.37 sin23t | 1.38 tsh5 t | 1.39 t sin2 t |
| 1.40. 2t - 5t | 1.41. t2-3t+7 | 1.42 cos22t |
| 1.43. t2sh2 t | 1.44 t cos2 t | 1.45. t3 |
| 1.46. te -3t | 1.47. 3t - 2t2 | 1.48. 7 t –cos3 t |
| 1.49. t cos2 t | 1.50. t sin2t |
Задание 2. Найти изображения следующих функций:
| 2.1 | a) 2sint-cos3t | б) t2cost | г) sin(t-2)h(t-3) |
в) 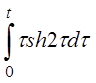
| д) 
| ||
| 2.2 | a) t2et | б) t2sint | г) cos(t-3)h(t-2) |
в) 
| д) 
| ||
| 2.3 | a) 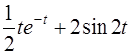
| б) t2sht | г)sin(t-3)h(t-2) |
в) 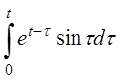
| д) 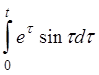
| ||
| 2.4 | a) t-sin3t | б) t2cht | г) cos(t-2)h(t-1) |
в) 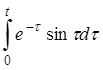
| д) 
| ||
| 2.5 | a) t+2sin3t | б) t2cost | г) et-2h(t-1) |
в) 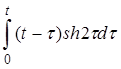
| д) 
| ||
| 2.6 | a) e2tsint | б) t2sin2t | г) th(t-1) |
в) 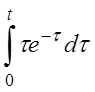
| д) 
| ||
| 2.7 | a) etsin3t | б) t2ch2t | г) th(t-2) |
в) 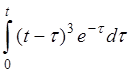
| д) 
| ||
| 2.8 | a) e2tcos3t | б) t2sh2t | г) (t-1)h(t-2) |
в) 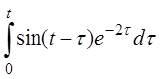
| д) 
| ||
| 2.9 | a) t3+sin3t | б) t2sh3t | г) sin(t-1)h(t) |
в) 
| д) 
| ||
| 2.10 | a) cos2t | б) t2sin3t | г) (t-3)h(t-3) |
в) 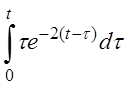
| д) 
| ||
| 2.11 | a) sin2t | б) t2cos3t | г) (t+2)h(t-1) |
в) 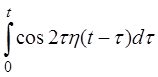
| д) 
| ||
| 2.12 | a) 4t2cos2t+sh2t | б) e2cos2t | г) eth(t-1) |
в) 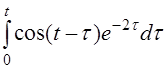
| д) 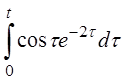
| ||
| 2.13 | a) tet+cht | б) t2ch3t | г) et+2h(t-1) |
в) 
| д) 
| ||
| 2.14 | a) (t+1)sint | б) costcos3t | г) sinth(t-3) |
в) 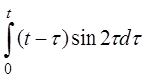
| д) 
| ||
| 2.15 | a) tsin5t | б) sintcos3t | г) costh 
|
в) 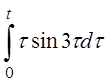
| д) 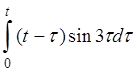
| ||
| 2.16 | a) tcost | б) etsin2t | г) sinth(t-  ) )
|
в) 
| д) 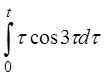
| ||
| 2.17 | a) tsin2t | б) etcos2t | г) costh(t-  ) )
|
в) 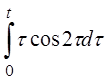
| д) 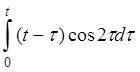
| ||
| 2.18 | a) t-sin2t | б) t4et | г) eth(t-4) |
в) 
| д) 
| ||
| 2.19 | a) t-cos2t | б) t2e-2t | г) (t-1)h(t-1) |
в) 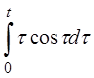
| д) 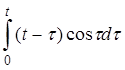
| ||
| 2.20 | a) t3+tcost | б) sin23t | г) th(t-2) |
в) 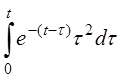
| д) 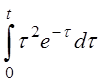
| ||
| 2.21 | a) tsh2t | б) cos2tcos3t | г) e2th(t-1) |
в) 
| д) 
| ||
| 2.22 | a) e5tcos3t | б) t2 sin4t | г) e3th(t-1) |
в) 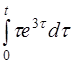
| д) 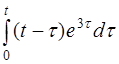
| ||
| 2.23 | a) e5tsin3t | б) tcos22t | г) e-2th(t-1) |
в) 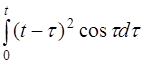
| д) 
| ||
| 2.24 | a) (t+1)sin3t | б) tsin23t | г) e-5th(t-2) |
в) 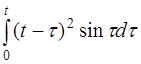
| д) 
| ||
| 2.25 | a) (t+2)sh3t | б) t2cht | г) th(t+2) |
в) 
| д) 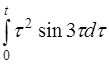
| ||
| 2.26 | a) (t+2)ch3t | б) t3e-4t | г) e3th(t-1) |
в) 
| д) 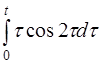
| ||
| 2.27 | a) cos22t | б) t3cos22t | г) et+1h(t-2) |
в) 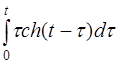
| д) 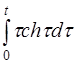
| ||
| 2.28 | a) sin32t | б) tsin22t | г) (t+1)h(t-2) |
в) 
| д) 
| ||
| 2.29 | a) tcost+t4 | б) t3e-5t | г) th(t-5) |
в) 
| д) 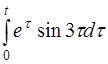
| ||
| 2.30 | a) e3tcost | б) t3e4t | в) t2h(t-3) |
г) 
| д) 
| ||
| 2.31 | a) cos32t | б)te–2t sin3t | г) (t-1)2h(t-2) |
в) 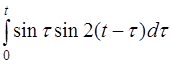
| д) 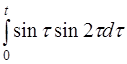
| ||
| 2.32 | a) 3sint-cos5t | б) t3sint | в) sin(t-2)h(t-3) |
г) 
| д) 
| ||
| 2.33 | a) t3et | б) t2sh3t | в) cos(t-3)h(t-2) |
г) 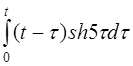
| д) 
| ||
| 2.34 | a) 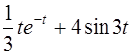
| б) t3cht | в) et-1h(t-2) |
г) 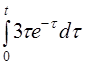
| д) 
| ||
| 2.35 | a) t-sin5t | б) t3cos3t | в) th(t-3) |
г) 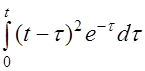
| д) 
| ||
| 2.36 | a) t+3sin2t | б) t3cost | г) th(t-3) |
в) 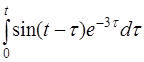
| д) 
| ||
| 2.37 | a) e4tsint | б) t3ch3t | в) (t-3)h(t-2) |
г) 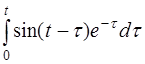
| д) 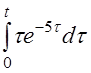
| ||
| 2.38 | a) etsin5t | б) t4sh4t | в) sin(t-2)h(t) |
г) 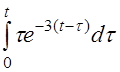
| д) 
| ||
| 2.39 | a) etsin5t | б) t2sh6t | в) (t-5)h(t-5) |
г) 
| д) 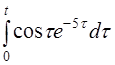
| ||
| 2.40 | a) t5+sin5t | б) t3sin2t | в) (t+1)h(t-2) |
г) 
| д) 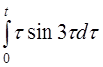
| ||
| 2.41 | a) sin23t | б) e3cos2t | в) et+1h(t-2) |
г) 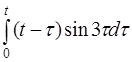
| д) 
| ||
| 2.42 | a) 5t2cos3t+sh3t | б) t2ch5t | в) sinth(t-4) |
г) 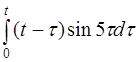
| д) 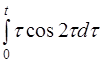
| ||
| 2.43 | a) 3tet+ch2t | б) cos5tcos3t | в) costh 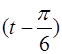
|
г) 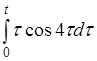
| д) 
| ||
| 2.44 | a) (t+7)sint | б) sin3tcost | в) sinth(t- 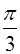 ) )
|
г) 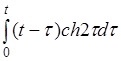
| д) 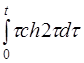
| ||
| 2.45 | a) tsin7t | б) e2tsin2t | в) e-5th(t-5) |
г) 
| д) 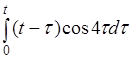
| ||
| 2.46 | a) t5-2sin2t | б) t3e-4t | в) th(t-4) |
г) 
| д) 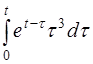
| ||
| 2.47 | a) t2-2cos2t | б) sin26t | в) e4th(t-2) |
г) 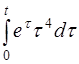
| д) 
| ||
| 2.48 | a) t2+tcos3t | б) cos2tcos5t | в) e4th(t-3) |
г) 
| д) 
| ||
| 2.49 | a) (t+3)sin5t | б) t2ch3t | в) e6th(t-4) |
г) 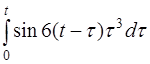
| д) 
| ||
| 2.50 | a) (t+1)ch7t | б)te–3t sin2t | в) et+2h(t-1) |
в) 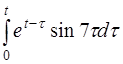
| д) 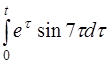
|
Задание 3. Найти оригиналы по заданным изображениям:
| 3.1 | а) 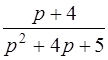 ; ;
| б) 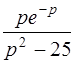 . .
|
| 3.2 | а)  ; ;
| б) 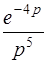 . .
|
| 3.3 | а) 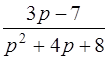 ; ;
| б) 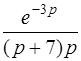 . .
|
| 3.4 | а) 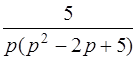 ; ;
| б)  . .
|
| 3.5 | а) 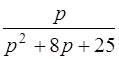 ; ;
| б) 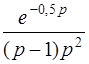 . .
|
| 3.6 | а) 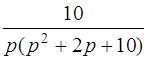 ; ;
| б) 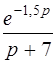 . .
|
| 3.7 | а) 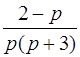 ; ;
| б) 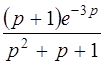 . .
|
| 3.8 | а) 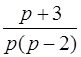 ; ;
| б) 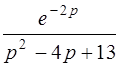 . .
|
| 3.9 | а) 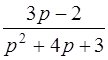 ; ;
| б)  . .
|
| 3.10 | а) 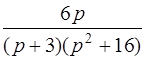 ; ;
| б) 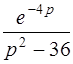 . .
|
| 3.11 | а)  ; ;
| б) 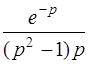 . .
|
| 3.12 | а)  ; ;
| б)  . .
|
| 3.13 | а)  ; ;
| б) 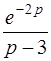 . .
|
| 3.14 | а) 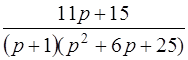 ; ;
| б)  . .
|
| 3.15 | а) 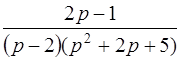 ; ;
| б) 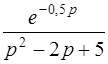 . .
|
| 3.16 | а) 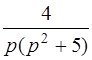 ; ;
| б) 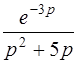 . .
|
| 3.17 | а) 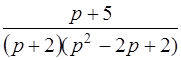 ; ;
| б) 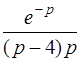 . .
|
| 3.18 | а) 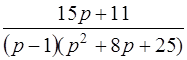 ; ;
| б) 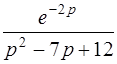 . .
|
| 3.19 | а)  ; ;
| б) 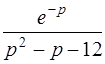 . .
|
| 3.20 | а) 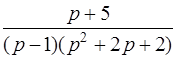 ; ;
| б) 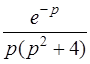 . .
|
| 3.21 | а)  ; ;
| б)  . .
|
| 3.22 | а)  ; ;
| б)  . .
|
| 3.23 | а) 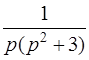 ; ;
| б) 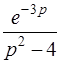 . .
|
| 3.24 | а) 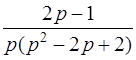 ; ;
| б)  . .
|
| 3.25 | а) 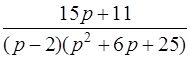 ; ;
| б) 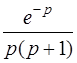 . .
|
| 3.26 | а) 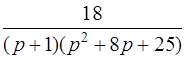 ; ;
| б)  . .
|
| 3.27 | а) 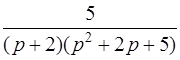 ; ;
| б)  . .
|
| 3.28 | а) 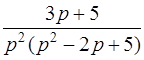 ; ;
| б) 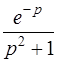 . .
|
| 3.29 | а) 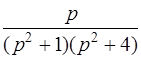 ; ;
| б)  . .
|
| 3.30 | а) 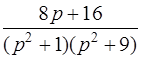 ; ;
| б) 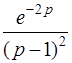 . .
|
| 3.31 | а) 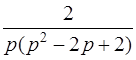 ; ;
| б)  . .
|
| 3.32 | а)  ; ;
| б) 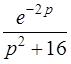 . .
|
| 3.33 | а) 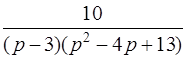 ; ;
| б)  . .
|
| 3.34 | а) 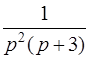 ; ;
| б) 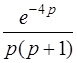 . .
|
| 3.35 | а)  ; ;
| б) 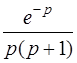 . .
|
| 3.36 | а)  ; ;
| б) 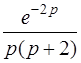 . .
|
| 3.37 | а)  ; ;
| б)  . .
|
| 3.38 | а)  ; ;
| б) 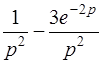 . .
|
| 3.39 | а)  ; ;
| б) 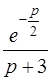 . .
|
| 3.40 | а) 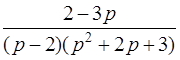 ; ;
| б) 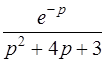 . .
|
| 3.41 | а)  ; ;
| б)  . .
|
| 3.42 | а) 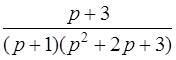 ; ;
| б) 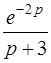 . .
|
| 3.43 | а) 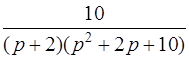 ; ;
| б) 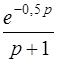
|
| 3.44 | а) 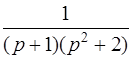 ; ;
| б)  . .
|
| 3.45 | а)  ; ;
| б) 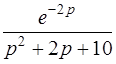 . .
|
| 3.46 | а) 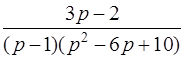 ; ;
| б) 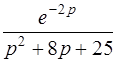 . .
|
| 3.47 | а) 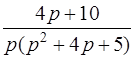 ; ;
| б) 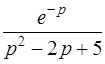 . .
|
| 3.48 | а)  ; ;
| б) 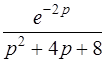 . .
|
| 3.49 | а) 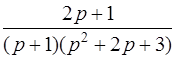 ; ;
| б)  . .
|
| 3.50 | а) 
| б)  . .
|
Задание 4. Операционным методом решить дифференциальные уравнения, удовлетворяющие заданным начальным условиям:
| 4.1 | 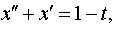 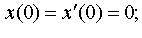
| 4.2 | 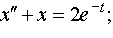 
|
| 4.3 | 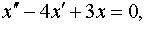 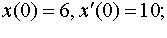
| 4.4 | 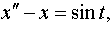 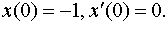
|
| 4.5 | 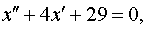 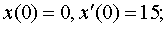
| 4.6 |  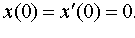
|
| 4.7 |  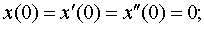
| 4.8 | 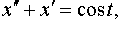 
|
| 4.9 | 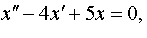 
| 4.10 | 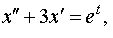 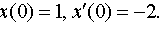
|
| 4.11 |  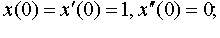
| 4.12 | 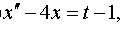 
|
| 4.13 | 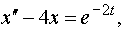 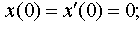
| 4.14 |  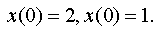
|
| 4.15 | 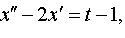 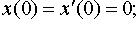
| 4.16 |  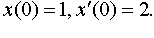
|
| 4.17 | 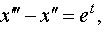 
| 4.18 |  
|
| 4.19 |  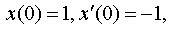
| 4.20 |  
|
| 4.21 | 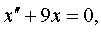 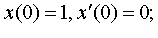
| 4.22 | 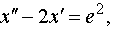 
|
| 4.23 |  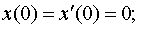
| 4.24 |  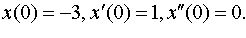
|
| 4.25 | 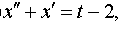 
| 4.26 |  
|
| 4.27 |  
| 4.28 |  
|
| 4.29 |  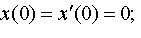
| 4.30 | 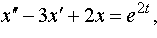 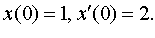
|
| 4.31 | 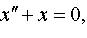 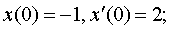
| 4.32 | 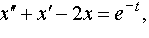 
|
| 4.33 | 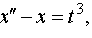 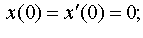
| 4.34 | 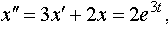 
|
| 4.35 | 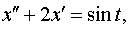 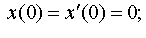
| 4.36 | 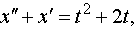 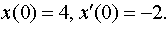
|
| 4.37 | 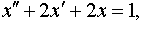 
| 4.38 | 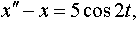 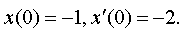
|
| 4.39 | 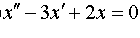 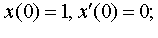
| 4.40 |  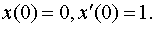
|
| 4.41 | 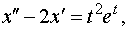 
| 4.42 | 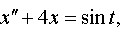 
|
| 4.43 | 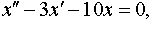 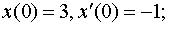
| 4.44 |  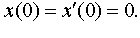
|
| 4.45 |  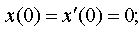
| 4.46 | 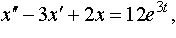 
|
| 4.47 | 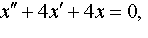 
| 4.48 | 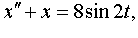 
|
| 4.49 |  
| 4.50 | 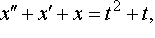 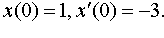
|
Задание 5. Решить систему дифференциальных уравнений:
5.1.  5.2.
5.2. 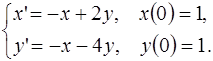
5.3.  5.4.
5.4. 
5.5. 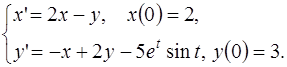 5.6.
5.6. 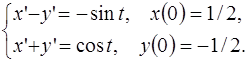
5.7. 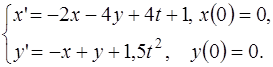 5.8.
5.8. 
5.9.  5.10.
5.10. 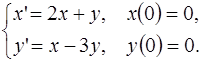
5.11. 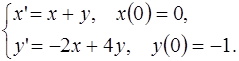 5.12.
5.12. 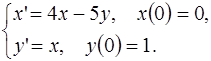
5.13. 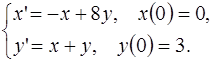 5.14.
5.14. 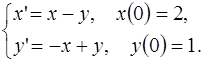
5.15. 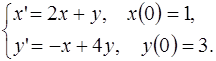 5.16.
5.16. 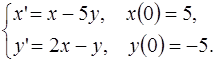
5.17.  5.18.
5.18. 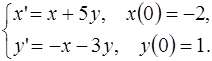
5.19. 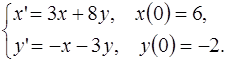 5.20.
5.20. 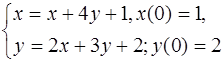
5.21. 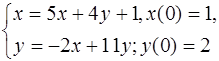 5.22.
5.22. 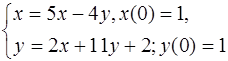
5.23. 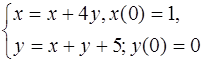 5.24.
5.24. 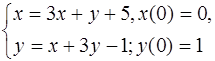
5.25. 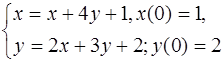 5.26.
5.26. 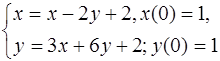
5.27. 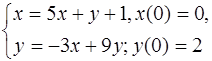 5.28.
5.28. 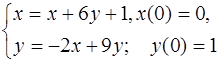
5.29. 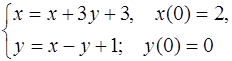 5.30.
5.30. 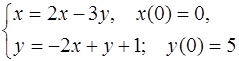
5.31.  5.32.
5.32. 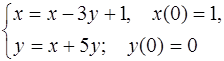
5.33. 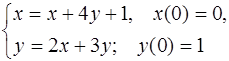 5.34.
5.34. 
5.35.  5.36.
5.36. 
5.37. 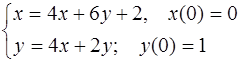 5.38.
5.38. 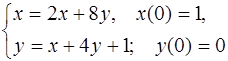
5.39. 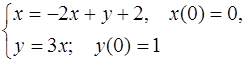 5.40.
5.40. 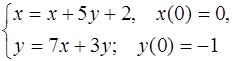
5.41. 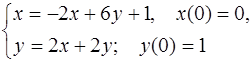 5.42.
5.42. 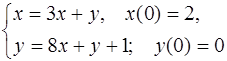
5.43.  5.44.
5.44. 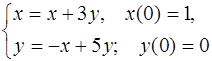
5.45. 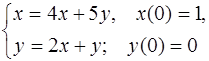 5.46.
5.46. 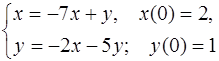
5.47. 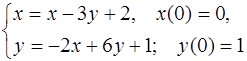 5.48.
5.48. 
5.49.  5.50.
5.50. 
ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАЧ
Пример 1: Пользуясь определением, найти изображение функции е2t.
Решение: В силу формулы (2) имеем

Пример 2: Найти изображение функции е2tsin 7 t.
Решение: Применяя формулу 9 из таблицы изображений при a =2, b =7, будем иметь
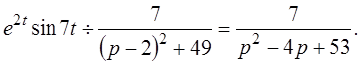
Пример 3: Найти изображение функции

Решение: Воспользуемся свойством интегрирования оригинала и результатом решения предыдущего примера, будем иметь
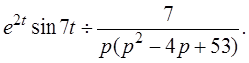
Пример 4: Найти изображение функции

Решение: Т. к. 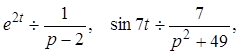 то в силу теоремы о свертке (см. (14)) будем иметь
то в силу теоремы о свертке (см. (14)) будем иметь
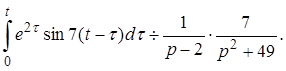
Пример 5: Найти изображение функции
е2tsin 7(t- 3)× h (t- 3).
Решение: Преобразуем выражение так, чтобы можно было воспользоваться теоремой запаздывания
е2t × sin 7(t- 3)× h (t- 3)= е6 × е2(t-3) × sin 7(t- 3)× h (t- 3)¸

Пример 6: Найти изображение функции
(t2 +1) е-t.
Решение: Используя свойство линейности и формулы 2 и 8 в таблице изображений, получим
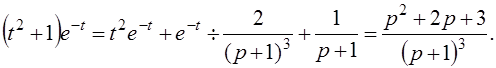
Пример 7: Найти оригинал функции

Решение: Представим данную дробно-рациональную функцию в виде суммы простейших дробей:
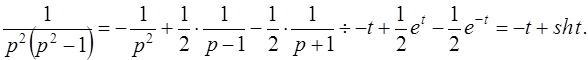
Здесь мы воспользовались формулами 2 и 3 из таблицы оригиналов.
Операционный метод особенно просто применяется к решению линейных дифференциальных уравнений с постоянными коэффицентами и систем таких уравнений. Рассмотрим это на конкретном примере.
Пример 8: Решить дифференциальное уравнение х²+х¢=е 2 t.
Решение: Пусть x (t)¸ X (p), тогда x¢ (t)¸ рX (p)-1, x¢¢ (t)¸ р 2 X (p)- р- 2, x¢¢¢ (t)¸ р 3 X (p)- р 2 - 2 р- 0 согласно свойству дифференцирования изображения, кроме того, 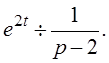 Тогда данное уравнение в изображениях примет вид:
Тогда данное уравнение в изображениях примет вид:

Разложив функцию Х (р) на простейшие дроби с помощью неопределенных коэффициентов, получим

Тогда решение х (t)=0,5+0,1 e 2 t+ 0,4cos t +1,8sin t.
Пример 9: Решить систему

при начальных условиях х (0)= х¢ (0)=1, у (0)= у¢ (0)=0.
Решение: Пусть x (t)¸ X (p), у (t)¸ У (p), тогда x¢ (t)¸ рX (p)-1, x¢¢ (t)¸ р 2 X (p)- р- 1, у¢ (t)¸ рУ (p), у¢¢ (t)¸ р 2 У (p), согласно свойству дифференцирования изображения. Перейдем к операторной системе
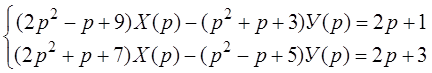
Для упрощения системы найдем сумму и разность ее уравнений:
 .
.
Отсюда
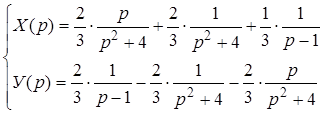 .
.
Переходя к оригиналам, найдем решение
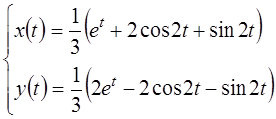 .
.
Дата добавления: 2015-10-30; просмотров: 138 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ОБЩИЕ УКАЗАНИЯ | | | Порядок проведения |