CTHOFO peffleHFl5J

ilpaBoll acm 3T0F0 BHHF15J

HO5IK BHHH5I

Ecirn y(O) = 1, TO CTHO pemeie BHHFI5I y’ — = 0 HMT BH

y=e 2x+1 y=e 2x—1 y=e 2x y=e —2x+1

O6wee pemee BHHH5I xy’ +2 in x = 0 HMT BM

y=21n2x+C y=—21n2x+C y=—41n2x+C y=—ln2x+C

Ec.rrn y(1) = 2, TO ‘-IaCTHOe pemee BHHWI xy’ — 3m2 x =0 HMT BH

y = in3 x +2 y=91n3x+2 y=6inx+2 y=31n3x+2

O6ee pemeHile — exy=e +C

—y=—e +c

y=2e +C

y = —e1 + C

ECJmy(1)=_,TO acoe pemee BHHH51 + 2e

y=2e

2

y = ex

2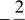

y=4e

e

O6ee pemee — Sin2 X = 0 JIMeeT BII

cOSx

y=3sin3x+C y=2sinx+C

sin3 x +c

sin3 x +c

Ec.nM y(O) = 1, TO ‘-IaCTHOe pemee BHHII5I e’ — X = 0 HMT BIIL

y = xe_x + e_x

y = _xe_x — e_x +3y = _xe_x — e —1y = —xe — e +2

Ec.nM y() = 2, TO ‘-IaCTHOe pemee BHHH5I cos2 x• — 2tgx = 0 HMT BH

y=2tg2x

y = 4tg2x—2

1 3

+—

cosx 2

y=tg2x+1

YpaBReRMe l3epHyJU[H 5{BJ15JTC5I C HMHHMMH upu

n=1 n=0 n=2

113 HHMX Lw1xjJepeHuHaJmHbIx ypaBHeHHH

1) y’=4 2)(3_x)_ysinx=ex;

xy dx

,

3)yy+xy

=cosx; 4)——Y --+7x+2y=O

dx

BHHH5{MH l3epHyJUlH 5IBJI5IIOTC5I TOJThKO

—3),4)

2)

—1),3)

—1),4)

PemeHiEieM,Lwfr1ePeHuHaJThHO1-O)IpaBHeHHSJ y’ — tgx = 1 5JBJ15ITC5I 4YHKUH5I

1

cosx y=tgx y=—tgx

y=ctgx

HHTeT-paJThHaSJ KpHBaSI, KOTO5I opeenne pemee ypaBFleFlua xy’ = y —1 lipH y(1) = 1,

MMT BM4

—A

—B

—C

113 HHMX lwcl)4)epeHuHaJmHbIx ypaBHeHHH

1) 2y’+3x2 +2y=O; 2) (x_y)dy=(3x+2y2x;

3) x2y’ + y —2 = 0; 4) yy’ — x2y = exy3

BHHH5IMH C Pa3LeI15IIOwHMHC51 HCCMHHMMH 5{BJT5IIOTC5I

—3)

—1),2)

—2),4)

—1),4)

PeuJeHileM Lw14)epeHuHaJmHoro ypaBueuwi y’ + 2xy = 2x 5JBI15ITC5I 4yHKuH5

y=1+ex y = e_X2

y = 1— eX2

y=1+e

HHTerpaJmHa5J KpHBa5I, COOTBTCTBY}OH45J pemeuio wjxJepeHuHaJmHoro BHHH5I

xy’ = y +3 HH y(1) = —3, ilMeeT BI1

—C

—B

—D

—A

y ex+1

PemeRMeM,Lw1xepeHuHaJmHoro BHHH5{ 3) + — = 51BJ15ITC5I (1)YHKUH5{

x x

y=nx+1

HHTerpaJmHa5J KpHBa5I, COOTBTCTBY}OH45J pemeio H4JepeHLI1aJTbHOFO BHHI45I

xy’ =y—4 HH y(2)= 6, MMeeTBML

-2

—A

—C

—D

—B

PemeRMeM,LwxepeHuHaJmHoro BHHH5I y’ + y = 3e2x 5JBJ15ITC5I YHKUH5I

—y=e —2x

y = e_X

—y=e —2x

—y=e 2x

+e x

+e —x

HHTerpaJmHa5J KpHBa5I, KOTO51 opeeiiei pemee BHHH5I (x — 2)y’ = y ripi y(O) = —4

HMT BH)

—B

—A

PemeHMeM,LwjxjepeHunaJmHoro BHHFT5J y’ + ctgx y = 1 5JBJ15JTC5I YHKUH5I

—y=ctgx+

—y=—tgx+

sin x

1

sin x

1 +1

cosx

y=—ctgx+ 1

sin x

113 HHMX w1)c1)epeHuHaJmHbIx ypaBHeHHH

1) (x —yy—ydx=O; 2)

e2

dy=xy2dx;

3)y’+4x2—y=O; 4)y3y’+x3(y+1)=O

BHHF151MF1 C P3CJ15IIOWHMHC51 HCMHHMMH 5JBJT5JIOTC5J TOJThKO

—1),3)

—2),4)

2),3)

—1),4)

PemeHileM,LHc1xepeHuHaJmHoro BHHH5J y — — = —i- 51B1[5ICTC5I 4YHKuH5I

x x

y=x 2 +

x

1

y=x 2

YHKUH f(x, Y)= BeTC OHOOHO YHKUH

Ro opica

6-ro HO5{K

1- ro HO5{K

2- o HO5{K

O6wee pemee BHHH51 y”= e2 HMT BH

y=1e2x +C1x+C7

y = + C1x+ C2

y = e21 + Cx

y = 4e2x + C1x+ C,

O6WeepemeHne BHHFT5I ))“ COS IlMeeT BII

y=—cos—+C1x+C,

4 2

1 x

y=——cos—+C1x+C, 4 2 -

y=4cos+C1x+C,

x v=—4cos—+C1x+C, 2

O6wee pemee BHHH51 Y” —s- MMT BII

y=—+C1x+C,

y=—1nx+C1x+C,

y=+C1x+C,

y = 1nx + C1x + C,

O6wee pemee BHHH5{ v”= e HMT BH

y=1e2 +C1x+C,

y=—4e2+C1x+C,

y=——e 2+C1x+C,

4 -

y=4e 2+C1x+C,

EcJ1M y(l) = 0, TO CTHO pemee BHHH51 xy’ — X = y HMT BHL

y = x1n(ex)

y = x1nx y = 1nx

x

YHKUH5I f(x,y) = — 3x2y + 5{BJ15{TC5I O,THOpO,THO 4YHKUHeH

8-ro HO5{K

6-ro HO5{K

3-ro opia

0-ro HO5J)K

O6ee pemeie BHHFT5I xy” —y’ = 0 JIMeeT BII

y =

C1x2

+ C2

y=+C1x+C,

y = 2C1x + C2

y=2x2 +C1x+C,

O6wee pemee BHHH5I xy” + = 0 IIMT BII

— y=C1x +C2

y=C11nx+C7

y = x2 + C1x + C,

y=—+C1x+C2

Ecirny(1) = 1, TO ‘-IaCTHOe pemee BHHH5I xy’ + X y HMT BH

y=xln—

e y=x1n

jx y=—x +2

=

y ex 2

O6wee pemee BHHH5I y” = sin2x HMT BH

y=4sin2x+C1x+C.,

1.

y=-sin2x+C1x+C,

y = —4 sin 2x+ C1x+ C2

1.

y=——sin2x+C1x+C,

O6wee pemene BHHH5I y’ + 2x = 2xy nMeeT BH

y=4x +

y = +1

y=x +C

y = e2x2 + 1

113 HHMX,LwjxjepeHunaJmHbIx ypaBHeHHH

1)

p 2x i

xy =y e —1;

2)

,

y

=T;

3)y2y’+x3y=O;

BHHF151MF1 C pa3.LeJ15IIomFTMFTc5I HMHHMMH 5JBJT5JIOTC5J TOJTbKO

—1),2)

1),3)

—2),3)

2), 4)

p	Y	Y
	x	x

113 HHMX.lrncl)cl)epeHuHaJmHbIx ypaBHeHHH

1)yy p +xy=O;

3)xy p +2y=y 2 e x; 4)2y p +3x2+2y=O

BHHF151MF1 l3epHyJU[11 5JBJI5JIOTC5J TOJThKO

—1),3)

2), 3)

— 2), 4)

—1),4)

TEMA 13..iIIfHelIHbIe JIfljjepeHIufaJIbHbIe BHHhISI 2-ro nopnjia C HOCTOSIHHbIMH

KO4PIfIufeHTaMII

O6ee pemel-me w1x1)epeHuHaJmHoro BHHH5J y” + a1y’ + a2y = f(x) co,LepIurr Be HOF13BOJThHbI IIOCTO5IHHM

— TH HO143BOJThHM HOCTO51HHM

OH HOW3BOJThHIO IIOCTO5JHHIO emipe HOF13BOJThHbI HOCTO51HHM

O6wee pemee OLHOpOLHOrO BHHH5J y” + + 9y = 0 MMT BHL

y = Cie_3x + C2e3x Y = (C1 + C2)e_3x Y = (C1 + C2x)e3x Y = (C1 + C2)e3x

BM ‘-IaCTHOFO pemeHH5J JIHHCHHOFO HeOLHOpOLHOrO H)PHUHJThHOFO ypaBHeHH5I 2-roHO51K C IIOCTO5JHHMMH KO3c1xHuneHTaMH 3BHCHT OT

BW HBO11 acm ii KOpHell xapaKTepllcTw-IecKoro BHHH5J

HOp51,LKa 3T0F0 BHCHH5I

o6wero pemewi oLHopoLHoro H)epeHuHaJmHor’o ypaBHeHI45I 2-ro nopia

HOF13BOJThHMX HOCTO5JHHMX

Ecrn

const

— peme BHCHH y” + a1y’ + a7y = 0 H — HCKOTOMC

HocTo5IHHbIe, TO o6wee pemee 3T0F0 BHHH5J HMCT BH

y=C1y1 +C2

YC1Y1 +C,Y2

Y(C1 +C2)/(Y1 ±Y7)

y = C1 + C,

Yi Y2

XapaKTepHcmecKoe ypaee JI5I I1HHeiiHOrO OLHOpOLHOrO BHHH5{ Y” + a1j/ + a2’ = 0

HMT BH

r2 + a1r = a2

r2 +r+(a1 +a2)=O

+ a1r + a2

a1r2 + a7r + 1=0

O6ee pemee O,THOpO,THOFO,TH4xepeHuHaJmHoro BHHH5I y” + — = 0 HMT BH,T

y = (C1 + C2x)e2x

y = Cie_4x + C2ex

y = C1 cos4x+ C2 sinx

y = C1 sinx—C2 cos4x

O6ee pemel-me O,LHOpO,LHOrO epeuaimoro BHHH5J y” — 8y’ + l6y = 0 neeBH

y = C1 cos 4x — C2 sin 4x

y=(C1 +C2x)sin4x

y=(C1 +C2x)e4x

—y=C1e —4x

4x

+C2e

O6wee pemee BHHH5I Y” — 4Y’ — 5Y = 0 MMeeT BM

Y = Cie_5x + C2ex Y = Cie_x + C2e5x Y = (C, + C2x)e4x

Y = C1 cosx+C2 sin5x

O6wee pemee BHHH51 Y” + 4))’ + 5)) = 0 HMT BH

Y = e_)x (C1 cosx+ C2 sinx)Y = ex(Ci cos2x+ C2 sin2x)Y = e)x(Ci + C2x)

Y=ex(Cl —2C,x)

O6wee pemee BHHH51 Y” 6Y’ + 13)) = 0 HMT BH

Y=(C1+C2x)e’

y=C1e +C2e

Y = e3x(Ci cos2x+C2 sin2x)

e(C1 cos3x + C2 sin3x)

O6ee pemee IIHHeHH0F0 oLHopoLHoro H)PHUHJThHOFO ypaBHeHH5Iy” +))‘ — 20)) = 0

MMeeT BH

Y = C1e5x + C2e4x

Y = Cie_5x + C2e4x Y = Cie_5x + C2e_4x Y = C1e5x + C2e_4x

O6wee pemene IIHHeHHOFO O,THOpO,THOFO,TH l4epeHUHaJTbHoFo BHHH5Iy”—2y’— 15y=OHMeeTBH

Y = Cie_3x + C7e_5x

y = Cie_3x + C2e5x y = C1e3x + C2e5x y = C1e3x + C2e_5x

O6ee pemene JmHeHHOFO OLHOpOLHOrO HjxepeHuHaJJbHoFo BHHI45I

y”— 7y’ + l2y = 0 MMT BII,L

—y=C1e —3x

—y=C1e —3x

—y=C1e 3x

—y=C1e 3x

—4x

+C2e

4x

+C2e

4x

+C2e

—4x

+C2e

O6wee pemee BHHF151 y” + 14))’ + 49y = 0 HMT BH

y = C1 cos7x+C2 sin7x

y = C1e7x + C2e_7x y = (C1 + C2x)e7x y = (C1 + C2x)e7x

O6wee pemee BHHH51 y” — l6y’ + 64y = 0 HMT BH

y = C1e8x + C2e_8x

y = C1 cos8x+ C2 sin8x

y = (C, + C2x)e8x

y = (C1 + C2x)sin8x

O6wee pemee BHHH51 y” + 8y’ + 25y = 0 HMT BH

e3x(Ci cos 4x + C2 sin 4x)

y = e3x(Ci cos 4x+ C2 sin 4x)

—y=C1e +C2e

y = e_4x(Ci cos3x+ C2 sin3x)

O6wee pemee BHHH51 3)” + l6y = 0 HMeeT BH

y = C1 cos 4x + C2 sin 4x

y=C/ 1 +C2xj ‘ e x

—y=C1e 4x

—4x

+C2e

y = e_4X (C1 cos 4x + C2 sin 4x)

O6wee pemee BHHH5{ 3) 3y = 0 BH

y = C1e3x

y=(C1 +C7)e3x

y=C1 +C2e3x y=3C1x

O6ee pemel-me BHHFT5I)‘ + 9j = 0 MMT BII

y = C1e3x + C2e_3x

y = C1 cos3x+C, sin3x

y = (C1 + C,x)e3x

y = e_3x(C1 cos3x+C, sin3x)

O6wee pemee BHHH5I)’ —16)’ = 0 MMT BM

y = C1 + C,e4x

y = (C1 + C,x)e4x

— y=C1cos4x+C,sin4x

y = C1e + C,e4x

O6wee pemee BHHH51 y” + 4y’ = 0 MMT BII

y = (C1 + C2x)e4x

y=(C1 +C2)e

y = C1 + C2e_4x

y = Cie_4x +

EcJ1M r1 = —2, r = 3 — KOH11 BHHH5I HKOTOOFO.IIHHeHHOFOOHOOHOFO Lw1xepeHuHaJmHoro BHHH5{ 2-ro Hop5ILKa C HOCTO5{HHMMHKo34x1?HLWeHTaMFI, TO HHO ypaee HMCCT BHL

—y” +y’—6y=O

—y”—y’—6 = 0

—y” +y’—6 = 0

EcJ1M r = 4 ± 31— KOpHH BHCHH5I HCKOTOOFO JWHCHHOFO OHOOHOFO wjxepeHuHaJmHoro BHCHH51 2-ro Hop5I,TKa C HOCTO5IHHMMHKo3c1?c1HuHeHTaMH, TO HHOC ypaee HMCCT BHL

—y”± 8y’+25y=O

—y,,—25y,+8y=o

—y,,—8y,+25y=o

+ 25y’ + 8y = 0

EcJ1H r1 = =4— KOHH BHHH5I HCKOTOOFO JIHHeHHOrOOHOOHOFO Lw1xepeHuHaJmHoro BHCHH5{ 2-ro HOp5I,TKa C HOCTO5{HHMMHKo34Jcl?HUHeHTaMH, TO,TaHHOe ypaee HMCCT BHL

—y”—8y’+ 16y=O

—y,,—4y=o

—y”+ 8y’+ l6y=O

O6ee pemee BHHFT5I 2y” + = 0 JIMeeT BIIL

y=e2x(Ci cos4x+C,sin4x)

y=Cie_4x+C,e4x

y=C1e +C,e

C cos2x + C2 sin 2x)

Ec.nn r1 = —3, r = —2 — KOH11 xapaepncmecoro BHHII5I HKOTOOFO JmHeHHOFO OHOOHOFO.Lw1x1epeHunaJmHoro BHHH5I 2-ro nop5I,LKa C HOCTO5IHHMMHK034J4JFIWIeHTaMH, TO HHO ypaene ilMeeT BH,L

—y”— 5y’ + = 0

+ = 0

+ 6y’ + = 0

—

Eciin r = 3 ± 5i — KOH11 xapaepncmecoro BHHH5I HKOTOOFO JmHeHHOrO OHOOHOFO,Lw14epeHuHaJmHoro BHHH5I 2-ro nop5ILKa C HOCTO5IHHMMH

Ko34x1HLweHTaMF1, TO HHO ypaene HMT BHL

—y” + + = 0

—y”+6y’+ l6y=O

—y”—6y’+ l6y=O

—y”— 6y’ + = 0

Ec.nn r1 = = —5 — KOHH BHHH5I HKOTOOFO JIHHCHHOFO

OHOOHOFO w1xepeHuHaJmHoro BHHH5I 2-ro nopa C HOCTO5IHHMMH

Ko3clxl?HUHeHTaMII, TO HHO ypaene HMT BHL

—y,,—5y,=o

—y”+ lOy’+25y=O

—y,,—5y=o

—y”— lOy’+25y=O

O6wee pemene ypaBHCHH5I 2y” — — = 0 neeT BH

y=C1e+C,e2 y=C1e +C7e

3 3

y=e (Acos--x+Bsin--x)

-

3 3

-

y=xe (Acos--x+Bsin--x)

---

Дата добавления: 2015-10-30