MMT BepTFIKaJmHyIO CHMHT0T

K1— K2

YriioM)BM5I H5IMMMH H3MBTC5J

MeHbIIII1H f OIL, H KOTOphIM Ha,Lo HOBHTh o6e H5JMM Lo ux coBnaLeHu5I C oci3io Ox

— MeHbfflMuI yrOIL,H KOTOphIM Ha,Lo HOBCHTb OH H5JMIO O ee coBnaLeHu5I C FOH

H51MOF1

— MHMJIHF1 yroJi, Ha KOTObIH Ha,Lo HOBCHTh o6e H5IMM O fix COBnaLeHH51 C OCMO 0))

— 3HOCTb yrILOB, O6pa3OBaHHbIX 3THMH H5JMMMH

YpaBliefille Hp5lMoFl, ilpoxowiwen epe HHIO TOK B HHOM HaHpaBJTeHHH, HMT BH

(x2 — x1)(— = (2 —1)(x — x1)

ab

—y —yo=Ko(x — xo)

B BHHH11 H5IMbIX C L1HTPOM B TOK A yrJIOBOH KO3c1xHuHeHT K —

cl?I1KCI1p0BaHHMH

6ecKoHeHbIii

HpOFI3BOJmHbIH

cera pae 0

YpaBliefifle H5IMMX C UHTPOM B TOT-lKe M0 (x0 HMT BH

—+=1

ab

Ax+By+C=O

ly—yo=K(x—xo)

YpaBliefifle Hp5IMoH B OT3KX HMT BHL

ab Ax+By+C=0

—y —yo=Ko(x — xo)

O6wee ypaee Hp5IMOH HMT BH,T

Ax+By+C=0

ab

—y —yo=Ko(x — xo)

YpaBReHile Hp5lMoH, llpoxo5JweIi epe TOKH A(—2;3) Fi B(4;—3), ilMeeT BH,L

y=—x—5 y=—x+1 y=—2x+1

PaccTo5lHMe OT TOK1kI O H51MOFI ollpe,LeJ15IeTc5I c1OPMYJIOH

d=(x2 —x1)2 +(y2 —y1)2

d= Ax0 +By0 +C

A2 +B2

d_0 +By0 +C

-

A2+B2

d= °_+By0 +C

A2 +B2

YrI1oBoii KO34x1HLweHT H51MOF1 Ax+By+C=O ripi B O pae

A B

A

B

TaHFeHC yriia HKJIOH np5IMOcI + = 1 K OCH Ox pae

ab

b

a

a

b b

a

YpaBHeHMe Hp5IMoH, poxownue epe TOK A(1;2) apauiemo Hp5IMOH x + y —1 = 0,

HMT BH

y=—x+3 y=—x—5

y=—x—3

YpaBHeHHe IIpnMoM, HpoxowIwen epe TOK A(—1;2) HePHeH.IWKYJmPHO H5IMOF1

y = 2x +3, ilMeeT BII,R

y=——x—3

1 3

2 2

1 2

y=——x+—

2 3

1 3

2 2

B Tpeyl-OJThHIkIKe C BepfflHHMH B TO’ucaX A(—1;1), B(1;2), C(3;—2) ypaBHeHue MC4I$HM AM

HMCCT BH4

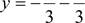x2

x3

y =——+—

x

x2

B TFOJThHF1K C BCpHIHHaMH B TOKX A(—1;1), B(1;2), C(3;1) ypaee Hp5IMOH AC

MMT BII,T

y=x

y=1

x=1

y=x+1

Hp5IMa5

xy

—+-—=1,re

ab

a O Fi b O

apauiema oci Ox

apauiema OCFi Oy

epeceae oc Ox B TOKC (a;O) epeceae OCh Oy B TOKC (a;O)

YpaBReRMe Hp5IMoH, poxownue epe TOK A(2;3) Fi o6pa3yloweii c HOY1O)KHTJThHMM

oci Ox yroi 450, HMT BHL

y=x

y=x+5 y=x—2 y=x+1

YpaBHeHHe Hp5lMoFl, HpoxoJweIl epe TOK B(4;1) Fi o6pa3yIowei c HOY1O)KHTJThHMM

HaHpaB.TIeHI4eM oci yroi 1350, MMT BML

x+y—5=O x—y—3=O x+y—3=O

— —x+y—5=O

K H51MOF1 y = —4x + 1 H5JM5I

— y=——x+2

— y=—x+2

y=4x+2

— y=—4x+3

Yro.ri Meicy H5{MMMH 2x + 3y —4 = 0 Fi 3x — 2y +1 = 0 paeii 00

YpaBReRMe Hp5IMoM, poxoiwe epe TOKH A(x1,y1) Fi B(x,,y2), HMT BHL

y—y1

=

x—x1

Y2 Yi X2 —X1

Y2 +1

X2 +X1

=

YYi X—X1

y—y1

=

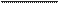x—x1

X2 —X1 Y2 Yi

YY2 XX2

Y2 Yi X2 —X1

PaccTwrnlle OT TOKH A(2;—1) o Hp5JMOH 4x — 3y +9 = 0 BHO

—2,8

—4

—14

—7

113 H51MMX

a)x—5y—3=O; 6)5x—y+4=O; B)5x+y—3=O; r)x+5y+3=O Hapaiii1eIIbHokK

Hp5IMOFI y = 5x —3 6y,LeT

a)

B)

r)

6)

113 H51MbIX

a)2x+y—3=O; 6)x+2y—3=O; B)2x—y+5=O; r)x—2y+3=O

HepHeHW1KyI151pHOM K Hp5JMOH y = —2x +3 6y,LeT

a)

—6)

r)

B)

TOTIKaMF1 epeceewi Hp5JMOH 3x — —12 = 0 C OC5IMH KOOpLHHaT Ox H Oy 5IBJI5IIOTC5I

COOTBTCTBHHO TO’-IKH

A(4;0) Fi B(0;—3)

A(0;—3) Fi B(4;0)

— A(—4;3) Fi B(3;—4)

A(—4;0) Fi B(0;3)

YpaBHeHHe Hp5IMoFl, poxowiwe	epe TOKH A(2;3) Fi B(2;—1), HMCCT BH,L
—y=2x
—y=2
—x=2 —y=x—2

YpaBHeHHe Hp5IMoH, poxownue epe TOKH A(3;—1) Fi B(— 2;—1), HMCCT BHL

y=3x—2

Ecilil x2 = x1, TO BHCHHC Hp5IMoH, poxoiwe i epe T01IKH A(x1 y1) Fi B(x2 HMCCTBH

y—y1

=

x—x1

Y2Y1 x2—x1

x = x1

y = x1

y = k(x — x1)

Ecirn y2 = y1, TO Hp5IMon, npoxo,L5Ime I iepe3 TOKH A(x1 y1) Fi B(x,,; ilMeeTBH

y—y1 x—x1

Y2Y1 x2—x1

y=y1

y—y1 =x—x1

x = x1

4 3

Hp5lMMe y=—x+1 ii y—x—2

—

—

o6pa3yloT fOI1 B 450

o6pa3yloT yFOJI, BHbW arctg

To’-wa M pa36HBaeT OT3OK AR, re A(1;2), B(4;5), TaK, T-ITO AM = 2 MB. KoopHHamI TO’-IKFI M BHM

(3;4)

(2;3)

(2;4)

(2,5;3,5)

PaccTo5lHMe OT TOKF1 M(3;4) o H5{MO y = 2x —1 BHO

1

YrI1oBoii KO3c1Jc1JHLWeHT Hp5IMOH 2x — —6 = 0 paeii 3

—3

Yroi HKI1OH Hp5IMoH 3x + 4y —1 = 0 K HOI1O)KHTJThHOM HHBJIHHIO OCH Ox pae

—arctgj­

3

—arctg—

arctgj­

3

arctg—

B TFOJThHF1K C BCpTJIHHaMH A(— 3;—2), B(2;3), C(4;—1) ypaee CTOOHM BC HMCCTBM

y=—2x+7

1 7

YjX+j

y=x+5

y = 4x—3

B TFOJThHF1KC C BCpHJHHaMH A(— 3;—2), B(2;3), C(4;—1) I1HH Me,LnaHbI AM paa

EcilM A(— 2;3), B(6;—3), TO TOK C, eiiua OTC3OK AR B OTHOTJICHHH KOOIIHTbI

(-3;3)

(-6;6)

AC

= —, HMCCT

CB

YpaBHeHMe Hp5IMoH, poxownue epe TOKH A(— 2;3) iT B(2;—1), HMCCT BHL

x—y+1=O x+y—3 = 0x+y—1=0 x—y—1=0

B TCFOJThHHKC C BCfflHHMH A(— 3;—2), B(2;3), C(4;—1) ypaieie BMCOThI CD HMCCT BH

x+y—3=0

x+y+3=O x+y+5=O x+y—5=O

B TFOJThHF1K C BfflHHMH B TOKX A(2;3), B(— 3;—2), C(4;—1))I1MH BMCOTM AD

Paa

7q1

5

TEMA 2. flpee.JibI II YHK1WI4

Ecilil lima(x) =0, TO YHKU1151 cL(x) H3hIBTC5I

x—*3

— 6ecKoHeHo 6ommoIi yHKu11en B TOK

x3

— 6ecKoHeHo Ma.nOFl c1yHKLwe11 B TOK x = 3

— HOCTO5IHHOH B TOT-W x = 3

y6blBaloweui 4yHKu11eH B OKCTHOCT11 x = 3

EcliM 6ecKoHeHa51 11CJ1OB5J nOCI1e,LOBaTeJmHOCTb {a } 11MT 11pe,LeI1 a, TO 8 — OKCTHOCTbTOKH a COepK11T

6ecKoHeHoe ‘-IMCJIO q.neHOB 11OCI1OBTJThHOCT11

KOHeT-IHOe TI11CJ1O q.TIeHOB 11OC.neLOBaTeJmHOCT11 6ecKoHeHo aioe T-IMCJIO T-UIeHOB 11OCJIe,LOBaTeJmHOCT11 OBHO fl q.TIeHOB

2x2—x—3

Hpeeii urn pae

x-*-13x +2x—1

5

5

5

4

5

KaKoe 113 yTBep)KLeH11H BepHO?

Ec.nM 11OCI1OBTJThHOCTb HMT Hpe,LeI1, TO OH MOHOTOHH

Ecjw 11OCI1OBTJThHOCTb M0H0T0HHa, TO OH CXO11TC5I

Ec.nM 11OCI1OBTJThHOCTb MOHOTOHH 11 orpaHHeHa, TO OH HMT npeeii

EcliM 11OCI1)OBTJThHOCTb CXO,LI11TC5{, TO OH 3HKOHOCTO51HH

BbIpaeHHe cc — ciD

BHO 0

—paBHO

BHO

—

5IBJ15{TC5{

ECJIH uirn f(x) TO c1JYHKUH5{ f(x) H3MBTC5I

—*

6ecKoHeHo Malloll BeIlHqHHOH B TOK x =

6ecKoHeHo 6omuioii BeJIHqHHOH B TOK X =

HHMBHO11 B TOK X =

KOHCTaHTOH

Hpeeii Llfllsa pae

a—>O a

—cc

—1

Hpeeii HOCTO5IHHOii C 0 pae

— CMO11 HOCTO5IHHOFI pyrOH HOCTO5JHHOFI

Hpeeii HpOF13Be.LeHw1,LByX 4yHKuHH pae

cyMMe Hpe,LeJIoB 3THX 4)YHKUHH

3HOCTF1 peeiio 3THX cyHKunHHOM3BHMIO peeio 3THX 4yHKuHHOTHOII1HF1IO peeio 3TFIX 4yHKuHH

41115{ CYWCTBOBHH5I npeLeJ1a YHKUHH f(x) B TO’-we X0, BHOFO ‘-iciiy a 0, Heo6xoLHMo

Fi,LocTaToqHo, To6M B HKOTOOF1 OKCTHOCTH TO’-IKFI X0 ilpil yciloBilil, TO a(x) —

6ecKoHeHo MaJIa5{ c1yHKUH5{ B TOK X0

f(x)=a(x)

f(x)=a+a(x)

f(x)=a.a(x)

a

a(x)

Hpeeii

( i

+ pae

l1fl1I1

8— OKCTHOCTMO TOKH a H3MBTC HHTepBan I1HHOH 8 C UHTPOM B TOK aHHTepBan I[HHOH 26 C UHTPOM B TOK aHHTCBfl I[HHOH 26, coep)KawHH TOK 0HHTepBan J1HHOH 6 C UHTPOM B HJ1

Ecim 6ecKoHeHa qMcI1oBa HOCIIe,OBaTeJThHOCTh {an } MMT Hpe,eJ1 a, TO BH 8 —

OKCTHOCTH TOKH a COKMTC5J

KOHHO qilCilO ee qileHOB

— 6ecKoHeHoe ‘IHCIIO ee T-LTIeHOB

— 4HIKCF1pOBaHHOe tWCIlO qIleHOBOBHO fl T-LTIeHOB

2x2—7x+3

Hpeeii Tim pae

3x —lOx+3

5

5

5

1’

Hpeeii 1im 1— — pae

n)

5

e3 e15

5

Ec.nH q.neHbl HocI1e)oBaTeJmHocTeH {an }, {bn }, {cn } ripFi mo6Mx n e N OBI1CTBO5IIOT

an bn

c,,, ii Tim a,7 = Tim c, = a, TO

fl—>D fl—>D

Imb

n—*cID

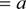limb,1

n—*cf

Limb,1

n—*cIJ

limb,1 <a

Eclill urn a, = a, urn b, = b Fi I15J rno6Mx n N BMHOJ1H5ITC5I HBHCTBO a, b,, TO

fl-* fl-*

ab a<b a b

a b

(i’ Hpeeii Timl+jJ PBH

5

5

e3

e5

urn

2x3—x2+3

Hpeeii -, pae

x-°° 3x +x—2

—3x2+x—2

Hpeeii Tim pae

x-> 4x —1 lx +3

—0

3x2—5x+7

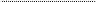Hpeeii Tim pae

x-*c4x +2x—5

—c/D

5

5

sin3x

Hpeeii 1111 pae

—3

—0

sin x

Hpeeii lim 2 pae

x—*O x

—0

/

Hpeeii Tim(1+ I pae

X->D\

e3 e3

x

I

Hpe,reii urnt I pae

X*QC\ 2xJ

e3

e4

3X 4

Hpeeii Tim pae

4X +5

x_*oo

—0

5

—3x+2

Hpeeii Tim pae

x- 2x+3

2

Ecrni HH x x0 YHKUH a(x)— 6ecKoHeHo MaJ1a BJlHHH, TO

paa 6ecKoHeHocm 6ecKoHeHo 6oJmma5I ernina

— HOCTO51HH51 Be.nwrnHa

BJ1FIHH

a(x)

Ecrn HH x x0 YHKUH f(x) — 6eCKOHeHO 6obma BernlqnHa, TO

paa HJT[O

HOCTO51HH51 Be.rlwrnHa 6eCKOHeHO MJ15I BJ1HHH

BeJlw-lHHa

f(x)

Ec.nH B OKCTHOCTH TO’-IKH X0 HKOTOIO c1yHKuHIo f(x) MO)KHO IIpe,LCTaBHTb KK

f(x) = a + r,ie a— HOCTO51HHO IHCIIO, a(x) — 6ecKoHeHo MaJla5I BeJwqHHa upil x —*

TO 111T1 f(x) paieii

—a

a+a(x)

a huM a(x) B 3BHCHMOCTH OT OKCTHOCTH X0YKa3am Bblpa)KeHHe, KOTOO He 5IBJ151TC5{

(“0

()

YKa3am BMpa)KeHHe, KOTOO He 5IBJ15ITC5I

(“0

jim x2

pae

x—*3—O x2 —9

—-D

jim x2

pae

x—*3+0x2 9

—-cc

—0

—1

jim

3x

pae

x—*2—O 4 —

—-D

—0

—3

3x

Tim pae

x—>—2+O 4 —

—-D

—3

—0

lim(1 — 3x)x pae

x—*O

ECILH 6ecicoHeHo MaJTbI B TOqK X0 4JyHKUHH a(x) H f3(x) 3ICBHBaMeHTHM, TO urn

a (x)

—0

—1

cc

—A o,Ai

X—*Xo /3(x)

Ec.nH a(x) = e’ —1 Fi /3(x) = x —1 — 6ecKoHeHo amie B TOK x = 1 BeJIWIFIHbI, TO

CL(x) Fi [3(x) — 3KB14BJTHTHM

(1(x) — 6ecKoHeHo MJl5J BeJIIIqFIHa 6oiiee BMCOKOO Hop5JKa, ‘leM [3(x) (1(x) — 6ecKoHe’lHo MJl5J BJ1WIF1H 6oiiee HH3KOT’O Hop5JKa, ‘lM [3(x) (1(x) Fi [3(x) — 6ecKoHe’lHo amie BJ1WIHHM 3HMX HOp5JLKOB

EcilM a(x) = ln(1 + 4x) Fi /3(x) = 2x — 6ecKoHe’lHo amie BJ1W1I1HM B TO’lK x = 0, TO(1(x) Fi [3(x) — 3KBFIBaJIeHTHJil

CL(x) Fi [3(x) — 6ecKoHe’lHo aimie BJ1H’lHHM O,LHOFO HOp5JLKa

CL(x) — 6ecKoHe’lHo MJ15J BeJlw-IHHa 6oiee HI43KOFO Hop5JKa, qeM [3(x)(1(x) — 6ecKoHe’lHo MJ15J BeJlw-IHHa 6o.iiee BbICOKOFO Hop5JKa, qeM [3(x)

Ec.nM a(x) =1— cos3x Fi /3(x) = x3 — 6ecKoHe’lHo MJIM B TO’-lKe x = 0 BeIIHqFIHM, TO

(1(x) — 6ecKoHe’lHo Ma.iia5j BeJlw-lHHa 6o.iiee BbICOKOO Hop5JKa, qeM [3(x) (1(x) Fi [3(x) — 6ecKoHe’lHo amie BJ1W1HHM OLHOFO HOp5JLKa

(1(x) Fi [3(x) — 3KBMB3J1HTHM

(1(x) — 6ecKoHe’lHo MJI5J BeJIw-lHHa 6o.jiee HH3KOFO Hop5JKa, [3(x)

Ecrn a(x) = sin2 3x Fi /3(x) = 3x — 6ecKoHe’lHo amie B TO’-lKe x = 0 BeJIHqFlHbI, TO

(1(x) Fi [3(x) — 3KBF1BJ1HTHM

(1(x) — 6ecKoHe’lHo MJI5{ BeJIw-lHHa 6o.riee HH3KOFO Hop5{Ka, [3(x) (1(x)— 6ecKoHe’lHo MJI5I BJ1H’lHH 6oiiee BMCOKOO Hop5{Ka, ‘lM [3(x) CL(x) Fi [3(x) — 6ecKoHe’lHo amie BI[HqHHbI OLHOFO Hop5{LKa

EcJ1M CL(x) Fi [3(x) — 6ecKoHe’lHo amie B TO’lK x0 (1)yHKUHH 11

• a(x)

/3(x)

= 0, TO

(1(x) — 6ecKoHe’lHo aiia BI1H’lHH 6oiiee BbICOKOFO nopia, ‘lM [3(x)CL(x) Fi [3(x) — 3KBF1BJ1HTHM

CL(x) — 6ecKoHe’lHo aiia BejinqnHa 6oiiee HH3KOFO Hop5JKa, ‘lM [3(x)

cL(x) Fi [3(x) — 6ecKoHe’lHo amie BJ1H’lHHM OLHOFO Hop5JLKa

EcJ1M CL(x) Fi [3(x) — 6ecKoHe’lHo amie B TO’lK x0 (1)YHKUHH 11

• a(x)

/3(x)

= TO

a(x) — 6ecKoHe’lHo aiia BJIH’lHH 6oiiee BMCOKOFO opi,ijca, qe [3(x)ct(x) Fi [3(x) — 3KBHBJ1HTHM

ct(x) — 6ecKoHe’lHo aiia BeJIHqHHa 6ojiee HH3KOFO opi,ijca, qe [3(x)

a(x) Fi [3(x) — 6ecKoHe’lHo amie BJ1H’lHHM OLHOFO HOp5{,TKa

• a(x)

EcJ1H (1(x) Fl [3(x) — 6ecKoHe’lHo amie B TO’lK x0 (1)YHKUHH H /3(x) = A, re A 0,

A 1, TO

(1(x) Fl [3(x) — 3KBHBI1HTHM

(1(x) Fl [3(x) — 6ecKoHe’lHo amie BJ1H’lHHM O,THOFO HOp5{,TKa

cL(x) — 6ecKoHeHo Ma.r1a51 BJ1WffiH 6oiiee BMCOKOFO Hop5JKa, ieM [3(x)

cL(x) — 6ecKoHeHo Ma.r1a51 ernina 6o.jiee HW3KOT’O Hop5JKa, f3(x)

Ecirn a(x) = in sin x n /3(x) = 2x — — 6ecKoHeHo MJThI B TOT-we X — BeIlHqMHbI, TO

cL(x) n 13(x) — 3KBHBJ1HTHM

— cL(x) — 6ecKoHeHo MaJla5J erniqna 6oiee HH3KOFO HOp5JKa, ‘leM 13(x)

cL(x) n [3(x) — 6ecKone’lHo amie BeJIH’-IHHM O,LHOT’O Hop5JLKa

cL(x) — 6ecKoHe’lHo MaJla5J BeJIW-lHHa 6oiee BMCOKOO Hop5JKa, ‘-leM [3(x)

Hpeeii urn

1—cos22x

pae

x-*O 3x2

• sin3x

Hpeeii urn pae

xO x +4 —2

2 pae

Hpeeii u•rn x3+x2—2x

x-*1 x —3x+2

—0

——3

• 5n 2

Hpee 1im +3

X3_42

pae

xsin2x

Hpeeii urn pae

x-*O 1—cos2 x

Hpe,reii tim (‘/x2 + 2x — x) pae

x—÷+

HpeeM

• sin5x e4x_1

pae

5

4

5

4

e5X

Hpeen urn pae

x—*O 1—cos3x

5

5

—cc

TEMA 3. HenpepblBllocm yHKuHH. To’IKH 3bIB H CHMHTOTM ICllBbIX

YHKU115{ y =J(x) H3MBTC5J H11MBHOH B TOK X0, ecrni

oHa CyWeCTByeT B OKCTHOCTH TOKH X0 CYWCTBYT KOHHMH 11pe,LeII urn J(x)

x—>xo

— CYWCTBYT KOHeqHMH 11pe,LeJ1

urn J(x)=J(xo)

x—*xo

oHa CLUeCTBeT B TOK X0 11 B ee OKCTHOCT11

ToKa x0 iis c1yHKu1111f(x) 51BJ15JTC5J TOqKOH papia 1 -rOpo,La C KOHHMM cKaqKoM, eciTHXOT5I 6b1 O,L11H 113 O,LHOCTOpOHHHX npeLeY1oB urn J(x) iuii urn J(x) pae KOHeT-IHOMy

x_*xo_o x_*xo+o

qHc.Tly

KOHe’-IHJile OHOCTOOHH11 pe,eiii urn J(x) urn J(x)

x_*xo_o x_*xo+o

CYWCTBYIOT KOHe’-IHMe O,LHOCTOpOHHHe pe,eii urn J(x)H urn J(x)

x_*xo_o x_*xo+o

XOT5I 6M O11H 113 O,LHOCTOpOHH11X npeLeY1oB B TO’-we Xo 6ecKoHeeH

To’-wa x0 iii c1yHKuH11f(x) 51BJ15JTC5I TOT-IKOH papa 2-ro po,La, CJIH

XOT5I 6M OHH 113 OLHOCTOpOHH11X npeLe.r1oB urn J(x) H urn J(x) 6ecKoHeeH

x_*xo_o x_*xo+o

XOT5I 6M O,LHH 113 OLHOCTOpOHHHX Hpee.lloB urn J(x) H urn J(x) pae KOHeT-IHOMy

x_*xo_o x_*xo+o

HCJ1

KOHe’-IHJile OHOCTOOHHH peeiii urn J(x) = urn J(x)

x_*xo_o x_*xo+o

KOHe’-IHJile OHOCTOOHHH pe,eiii urn J(x) urn J(x)

x_*xo_o x_*xo+o

Fpa4rnK 4JyHKUHH y =J(x) HMT BTHKJThHIO CHMHTOT X = X0, CI1HCYLUCTBYT

LimJ(x)

TO’-wa X0 5{BJI5{eTC5{ yCTpaHHMOH TOqKOH papia viJ(x)

TO’-wa X0 5{BJI5{eTC5{ TO’-IKOH papia 2-ro poa (c 6ecKoHeHbIM cKaKoM) TO’-wa X0 5{BJ15{TC5{ TO’-IKOH papia 1 -ro poa (c KOHCHbIM cKaKoM)

ECIIH 4JYHKUH5I y = f(x) B TOK X = X0, TO

oHa opeeiiea B TOK

oHa MO)ICT 6Mm H oHpeeY1eHa B TOK

opeeiiea B3C B OKCTHOCTH TOKH X0, KOM caMoll TOKH X0

limf(x)=co

x—*xo

Ec.nH 4YHKUH5I f(x) Ha OT3K [a;b] H H KOHUX 3T0F0 OT3K HHHHMT 3HHH51 3HbIX 3HaK0B, TO

HaHeTc51 XOT5I 6M O)H ToqKa c e (a;b), B KOTOOH YHKUWI o6pamaeTc5l B 0

HH B OHOM TOqKe HHTBI1 (a;b) 4YHKUH51 f(x) He o6pamaeTc5l B 0

— BO BCM HHTBI1 (a;b) 4JYHKUH5I f(x) HOI1O)KHTJThH

— BO BCM HHTepBaJIe (a;b) 4JYHKUH5I f(x) OTPHUTJThH

EC.TIH c1)YHKUH5I f(x) Ha OT3K [a;b], TO OH

— MO)KT 6bIm Ha O)HOM 113 KOHUOB OT3K [a;b]

MO)KT 6bIm BHTH HHTBJ1 (a;b)

H CBepXy, 11 CH113

— orpaiea HuH cBepxy, 11.1111 CH113

HpHpaweHHe c1yHKuHH y = f(x) Ha OT3K [x0, x0 + Ax] HaXOLHTC5J HO 4)opMyue

f(x0 -Ax)-f(x0)

f(x0 +&)+f(x0)

f(x0 + Ax) - f(x0)

f(x0 -Ax)+f(x0)

YHKUH51 B TOK, eculil

6ecKoHeHo MI[OM HPHPWHHIO apryea COOTBTCTBT HO113BOJThHO nppaweecFYHKUHH

6ecKoHeHo MJIOM 1lpHpaWeHHIO 4YHKu11H COOTBTCTBT 6ecKoHeHo 6oimmoe

ppawee apryea

6eCKOHe’-IHO MJIOM HP11PWHHIO apryea COOTBTCTBT 6ecKoHeHo auioe pipawee 4JYHKUHH

6ecKoHeHo Ma.rlOMy HPHPWHHIO apryea COOTBTCTBT 411KCHpOBaHHOe

pipawee 4YHKUHH

IYHKUH5I B HHTepBaJIe, eculH oHaHa ero KOHUX

HMT KOHe’-IHOe ‘-IHCI[O TO’-IeK papia 1-rOpoa Ha 3TOM 11HTBJ1

HMT OH TO’-Wy papia 1-rOpoa B 3TOM 11HTBJ1

B Ka)K)OH ero TOqKe

To’-wa papa C KOHHMM CKKOM — 3T0 TO)K caMoe, TO

TO’-wa papia 2-ro poa

TO’-wa CTHHMOFO papia TO’-wa papia 1-ro poa

TO’-W, B KOTOpOH HpOH3BOLHa5I cJYHKUH11 KOHH

YruOBOii KO3c1J4JHUHCHT HaKuOHHOH CHMHTOTM HaXOLHTC5{ HO cjopMyuIe

kLjrnf(x)

x—*co

k=Li,E

kLim

x f(x)

f(x)

x—*O X

f(x)

kLim

X—*ci X

Y POF13OHTJThHOH CF1MHTOTM y = kx + b

— k O,b O

— k O,b=O

k=

k=O

Ec.TIH cj?yHKUWI f(x) B TO’-IKe Fi f(x0) 0, TO B 6ecKoHeHo MayloHOKCTHOCTH TOKH X0 c1yHKuH51 f(x)

o6paLuaeTc5I B 0

HMT TOT)K 3HaK, T-ITO Fi f(x0)

HMT HOH3BOJThHMF1 3HK

MH51T 3HK C

<<>> Ha

<<+>>

EC.TIH B TO’-we X0 CYWCTBYIOT He BHbI M)KLY CO6OH KOHHM.JTeBbIH H upaBbIll peemi cj?yHKUHH, TO

— TO’-wa papa 2-ro poa

— TO’-wa papia 1-P0poa

— CTHHM5{ TO’-wa papia

B TOT-we X0 HpOH3BOLHa5I 3TOH YHKUHH

ECIIH B TO’-we XOT5I 6M OLHH H3 OLHOCTOpOHHHX HpeLey1oB HKUHH 6ecKoHeqeH, TO

— TO’-IKa papia 1-P0poa

— CTHHM5{ TO’-wa papia

— TO’-wa papia 2-ro poa

B TO’-we He CYWCTBYT BTHKJThH5I CHMHTOT

x—3

IYHKUH5{ y = HMT BTHKJThHIO CHMHTOT

x —4x+3

x=1

x = 1,x = 3

x=3

y=1

YHKUH =

— 4x

HMT BCTHKMbHIO CHMHTOT

x=4

x = O,x = 4

x=O

y=x+2

Hycm Tim f(x) = —2, Tim f(x) = 2, ‘ror,ia CKa1OK 4YHKUHH f(x) B TO’-IKe X0 pae

x—*x0—O x—>x0+O

2x2+5x+6

4laHa 4YHKUMM y =. YTJIOBOH KO34X1MUHeHT HKJ1OHHOI1 CHM11TOThI pae

x—T

—cAD

—1

4IaHa cFYHKUHn y = 3x2 + 2x —5. YnroBoil KO34XFHUHeHT HaKIIOHHOfl CHM11TOThI pae

He CYWCTBYT

x2+2x—3

4IaHa 4YHKUHn y =. YpaBHeHHe HKJ1OHHOH CHMIITOThI uMeeT BH4

x

y=x—2 y=x+2

y=2

4aHa 4YHKUH5 =

X

x2 —4

YpaBHeHHe HaKHOHHOfl CHMHTOThI HMT BH

y=1 x=1

x=—2

x2+x e)THKUHS{ f(x) =

x —4x

x=O x=2

HMT CTHHMIO TOK B TOqK

He HMT CTHHMO11 TOKF1 papa

YpaBHeHHe HaK.TIOHHOiI CHMHTOTM LJ15J YHKUHH f(x) = ilMeeT BH,L

x +4

y=o

x2

y=x2 +4

2, ec.TIH x < —1;

411151 4JYHKUHH y= x2 +1,ecnH—1 x 1;

x +2, ec.TIH x> 1

— x = —1 — CTHHM5J TOK pa3pMBa; x = 1 — TOK papia 1-ro poa

— x = —1 — TOT-wa papa 1-ro poa; x = 1 — TOT-Wa papa 2-ro poa

— x = 1 — TOK papia 1-ropoa

TOK pa3plilBa HT

—x—3, ec.rIH x<—2;

21J151 c1yHKuHH y= 4—x2,ecnH—2 x 2;

x —2, ecn x> 2

x = —2 — TO’-Wa papa 2-ro poa; x = 2 — TO’-Wa papa 1-ro poa

x = —2 H X = 2 — CTHHMM TO’-IKH papia

x = 2 — TO’-wa papa 1-ro poa

x = —2 — TO’-wa papa 1-ro poLa

x+6, ec.riu x<—2; 4IJ15 4YHKUHH y= x2 —1,ec.riu—2 x<2;

—, ec.riu x 2

x

x = —2 — TO’-wa papia 1-ropoa

x = —2 — TO’-Wa papia 2-ro poa; x = 2 — TO’-Wa papia 1-ropoa

x = —2 H X = 2 — TOKH pa3plilBa 1-ropoLa TOqK papia HT

—x—5, ecii x —2;

JI5{ 4YHKUHH y= 1—x2,ecnH—2<x<2;

x -6, ecn x 2

x = —2 H X = 2 — TO’-IKH papia 1-ropo,Ta

x = 2 — TO’-wa papia 1-ropoa

x = —2 — TOK papia 1-ropoa; x = 2 — TOK papia 2-ro poa

x = —2 — TOK pa3pJ3IBa 1-ropoa; x = 2 — CTHHM5{ TOK papia

ecni x 1;

,111151 4YHKUMM 3) = 3x, ec.ri 1< x 3;

x +4, ecni x > 3

x = 1 — ycrpaiias ‘rornca pa3pMBa; x = 3 — ‘rornca papa 1-to poa

x = 1 — oqa papia 1-to poa; x = 3 — ‘rornca papa 2-to poa

—x = 1 FIX = 3 —ToqKH papia 1-to po,Ra

x = 3 — ToqKa papia 1-to poa

x2+2x—3

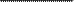YpaBHeHHe HIUIOHHOFI CFIMHTOTM,LJTh 4YHKUMM y MMT BH,R

x+1

y=x+1 y=x+2 y=x—3 y=x+3

YpaBReRMe HIUIOHHOFI CFIMHTOThI 41J151 c1YHKUHH y

y=3—x

y = 2x +3 y=2—x

3) = —x

3+2x—x2 x

HMT BH,L

eyHKuFI5l

x+1

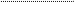= 2

MMT BepTFIKaJmHyIO CHMHT0T

x = —1

x=3

‘ x —2x—3

x = —1, x =3

y=O

eyHKUIDI Y

x2 —4x

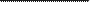= 2

x —3x —4x

Дата добавления: 2015-10-30