HMT YCTPHHMM T0KH 3bIB B TOKX

—X =—1, x = 0

= —1, x = 4

x = —4, x = 1

x = 0, x = 4

eyHKLWfl =

x=O x=6 x=3

2x —6 x2—3x

HMT TOK papa 1-topoia B TOK

He HMT TOKH papa 1-to poa

YHKUH5{ 3) = HMT CTHHMM TOKF1 B TOKX

x —4x

x = —2, x = 2

x = —2, x = 0, x = 2

x=2

— He HMT CTHHMMX TOK papia

2x+6

YHKUH51 y = HMT TOKH papia 1-ropo,La B TOKX

x —4

— He HMT

— x = —2, x = 2

— x = —3, x = —2, x = 2

2x —6

YHKUH5J y = B TO’-IKe x = 3 HMT

x +9

TO’-Wy papia 2-ro poaCTHHMIO TO’-wy papia He HMT TO’-IKH papia

HMT TO’-wy papa 1-ro poa

+

tYHKUH5{ y = HMT BepTHKaJThHMe CHMIITOTM (adilMuToTy)

x +x—6

x=2

x = —3, x =2

He HMT BepTHKaJThHMX CHMHTOT

2x2-i-3x—5

YpaBHeHHe HKJ1OHHOH CHMHTOTM,LI15{ 4YHKUHH y = HMT BHL

3—x

y = 2x —9

— y = —2x —9 y = —2x +9 y = —2x +3

TEMA 4. IHjHjepeHIUIaJIbHOe IIC’IIICJIeHIIe YHKUIIII OIHOII nepeeoit

Ec.LIH 4yHKUH5I y = f(x) B TO’-IKe MMT IIpOF13BO.LHyIO f’(x0), TO

f’(x0)=—

1im

f’(x0)=

Ax—* 0

—f(x0)= 1im-—

Av-*0Y

—f(x)= 1im--—

Ax-+0

Ec.LIH HOH3BOH51 c1yHKLwH f(x) B TO’-W X0 paa Hyjilo, T. e. f’(x0) =0, TO KCTJThH5I K

rpacjllucy c1yHKuHH B 3T011 TOT-IKe

OCFi Oy

oci Ox

He CYLUCTBYT

o6pa3yeT oCTpbIH Yf OJI C HOJ1O)KHTJThHMM ocu Ox

Ec.LIH cl?yHKUH5I y = f(x) Hc1x1ePeHuHPYeMa B TO’-IKe X0, TO OH 3bIBH B 3T011 TO’-IKe

B TO’-IKe

BO3CTT

y6bIBaeT

HpOH3BOHa51 4JyHKUHH y = paa

3sinx—1

3COSX 1n3

3smxlfl3COSX

3slflxlnsinx

4IH4x1?epeHuHaI1OM c1YHKUHH B TOK X0 H3MBTC5I HOH3BOH5{ c1JYHKUHH B 3T0 TOqKe

ppawee He3aBHCHMOH HepeMeHHoH

FJ1BH5{ I[HHeHHa5J acm HPHPWHH51 4JyHKUHH B 3T011 TOqKe

ppawee 4JyHKUHH B 3T011 TOK

HpOH3BOHa5I c1JYHKUHH y = Ji — 3x2 paa

3x

1_3x2

(1_3X2)3

3x
J1_3x2 1
2J1_3x2
wepeuai YHKUHM y= f(x)	B TOK X0 pae

dy = f’(x0)dx dy=f’(x0)

dy=

dx

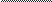f’(x0)

dY=f0)

dx

M4Jc1epeHuMaJI OT IIpOH3Be,LeHH5I (1)YHKLUIH u = u(x) Fi v = v(x) paieii

d(uv) = udv — vdud(uv)=vdu+udv d(uv) = vdv + udud(uv) = udu — vdv

4IMc1xjepeHuHaI[ BTOOFO llOp5ILKa 4YHKL1HH y = f(x) paieii

,,)

d 2 y=y iid2x d2y=y”dx dy=y dr

—a i2 y=ya i x

HpOM3BOHa5 c1JYHKUHH y = COS x paa

—sinx3

—sin3x

— 3x2 sin x3

——3x sinx

HpOM3BOHa51 c1JYHKUHH y = arcsin 2x parnia

Ji — 4x2

1

—

1_4x2

2

J1_4x2

2

1 + 4x2

HpOH3BOHa51 YHKUMM B TO’-IKe paa

THFHC yria HaK.nOHa K 0CM Ox HOMJ1M K KMBO11 B 3T011 TOKTHFHC yria HKJ1OH K 0CM Ox KCTJThHOM K KpMBOH B 3TOM TOKLT1 HKI1OH K 0CM Ox HOMaI1M K KpMBOM B 3TOM TOK

1J1HKI1OH K 0CM Ox KCTJThHOM B 3TOM TOK

HpOH3BOHa51 c1yHKww y = f(x) B TOK — 3T0

— CKOOCTb M3MCHCHM5I YHKUHH B TOK OTHOCHTJThHO W3MHHIIC c1yHKuHM B TOKC

CKOOCTh M3MCHCHM5J apryea OTHOCMTJThHO W3MHHMC apryea

HpOM3BOHa51 CI10)KHOI1 c1yHKuHH y = f(p(x)) paa

— f’(q(x))

f(q’(x))

f’(q’(x))

— f’(q(x))

Hp0M3B0Ha51 BT00F0 II0p5ILKa OT YHKUMH y = Sin x paa

sin x cos2 x

—Cosx

—sinx

Hp0M3B0Ha51 o6paTHoii 4YHKU1111 x = g(y) K 4YHKU1111 y = f(x) no opyiieg’(y) = -f’(x)

1

f(x)

f (x)

1

f’(x)

Hp0M3B0Ha5I c1JYHKUHH y = 1og x paa

1

x ax in a

x

1 x in a 1

x

HpOH3BOHa51 4YHKUMM =

— sin2 x cos x

1

cos x

1

ctg2x

ctgx

paa

HpOH3BOHa51 BTOOFO nop5I,LKa OT YHKUHH y = COS X paa

— COsx

sin2 x

—COsx

—sjnx

HpOH3BOHa51 YHKUHH y = paa

sin x

COSx

1

sin2 x

tgx

sin x ctgx sin x

HpOH3BOHa5I BTOOFO HOp5ILKa OT 4YHKUHH.Y in X paa

x2

x 2

—1

EcJ1H B HeKOTOpOii TOK x0 K KpHBOii y = f(x) HepHeHLHKyII5IpHa K ocii Ox, TO HOH3BOH51 B 3T0 TOK

paa HJTLO

paa 1

He CYTUeCTBYeT

HeHpepJIBHa

HpOH3BOHa5I c1JYHKUHH y =

tgx

paa

cos x

cos2 x

1

sin x

1

sin x

HpOH3BOHa51 c1yHKurn1 y = arctgx paa

1+ x2

arcctgx

—tgx

1

sin x

HpOM3BOHa51 c1yHKuHH y = aX paa

ax in a

a1na

_xa_X_

—a1na

4HddepeHuHan pae

dii dv

vdu — udv

udv — vdu

V

vdu + udv

V

H4J4JepeHuHan d(C + f(x)), re C — HOCTO5{HH5{ BenHqHHa, pae

C+f’(x)dx (C + f’(x))dxf’(x)dx

f’(x)

)jHflepeflqwan 4, 4y.iwipni y=In3x pae 3ln2xdx

x

—3ln2xdr

3m xctr

x

)jHddepemwan4, tyHI[ILHM)‘ = Sill2 X paBeH

—2coscfr

— —sin2x&

—sin2x&

—2sinx&

=

3HaeHHe HpOF13BOLHOM 4yHKLWF1 y

3/3— 2x 7

B TO’-we

HpOM3BOHa5 c1JyHKUHH = 31og3

Sfl X

paa

x3 1n3

—3sin 2 xcosx3cos 2 log3sin3x

—3sin2 xcosx

3HaeHMe HpOM3BOHOii cjyHKurn1 3) in3 X B TOK

e

3e

—0

H4J4JepeHuHaI1 4yHKUHH y	= esml2x	B TOK	=	pae
——2edx
——2dx —2edx

3HaeHHe HpOH3BOHOfi 4JYHKUHM y = ln(x2 — 2x) B TOK

HpOM3BOHa51 BTOOFO nop5I,LKa YHKUHH y = x2 in x paa

2lnx+1 2inx+3 2lnx+2

HpOM3BOHa51 BTOOFO Hop5I,LKa 4YHKUHH)) = X in X2 paa2

x

x

2+—

x

x

4Iwj4JepeHuHaI1 dy cl?yHKurn1 =

tgxdx dx

cos_ x dx

sln_ x

dx

sln_ x

ctgx

pae

HpOM3BOHa5 4YHKUHH y = Sin XCOSX paa

—cosxsinx

—cos2x

1.

——sin2x

cos2x

M4Jc1epeHuMaJ1 dy 4yHKWW y = tgxctgxpaBeH

ctgxtgxdx dx

-dx

w1JcjepeHuMaJ1 BTOOFO llOp5I,LKa YHKUHH y = c0s2 X pae

— cos2xdx2

— —2cos2xd2x

— cos2xd2x

—2cos2xdx2

HpOM3BOHa51 YHKUHH y = 3S

X paa

3SiflXlfl3sjfl2 sin2x.32x_1 2•3111n3•cosx

3sin2x

4IM4xjepeHuHaI1 BTOOFO Hop5ILKa d2y 4YHKLWH y = COSX Sin X pae

2sin2xdx2 2cos2xdx2

—2cos2xdx2

—2sin2xdx2

TEMA 5. IHjHjepeHUI4aJIbHOe Hc’IHcJIeHhle PyHKHIIII IBYX llMHHbIX (IpaIHeHT n llPOI13BOIHfl 110 HanpaB.JleHllIo)

Z4YHKUHH Z =x2 —xJJ—y3 +5 paa

2x——y3 2x——3y2

—2x—y—3y 2 +5

OHpeeI1eHHe aCTHOii HpOH3BO.LHOIi c1yHKLwH B TO’-we M0 (x0, y0) o epeeo X

BO3MOKHO, ecw c1yHKuH5I

opeeiiea TOJThKO B CaMOii TOT-we M0 (x0, y0)

opeeiiea TOJThKO B HeKOTOpOIi OKCTHOCTH TOT-1K11 M0 (x0, y0)

—He M0(x0,y0)

opeeiiea B TOK M0 (x0, y0) H B HeKOTOpOIi ee OKCTHOCTH

Ec.nH cl?yHKWUI Z = f(x, y). LBa)Kwil Hc134epeHuHpyeMa, TO

—z” z

—zif =z”

yy

—zif =z”

XX)J)

—zif =z”

Z4YHKUHH Z=x2—xfJ—y3+5 paa

— 3y2

—

2y

_x_3y2 +5

x2 —x—3y2

HoIrnbIii wcxjepeHuHaI1 cl?yHKUHH Z = f(x, y) oHpeLeINeTc5 HO c1OPMYJIe

dZ =(z +Z)dxdy

Z,dy

dZ = Zdx-Zdy

dZ=Zdx+Z,dy

Z4YHKUMM Z = — — + 5 paa

1

—0

Z4YHKUMM Z =x2 —xJJ—y3 +5 paa

1

1

—2— 1

—2x

HOJIHbIM wc1xjepeHunaJ1 BTOOFO Hop5ILKa 4YHKuHH Z = f(x,y) pae

Zdx2 +Zdy2 Zdx2 —Zdy2 (Zdx)2 +(Z,â5’)2

Zdx2 +2Z’dxdy+Z’dy2

Z, 4JyHKWW Z = x2 in 3) paa

2x+—

3)

2x

3)

2x

3)

x

3)

Z 4YHKUHH Z = x2 in y paa

2+iny

y

my

2 in y

PaBeHCTBO Z = Z nee MCTO,LI15I

— 4JYHKWW Z = f(x, y)

qeTHOll 43YHKLWH Z = f(x, y)

— rno6oii Ba){cLbI.LHc1xjepeHLwpyeMon YHKUHH Z = f(x, y) TOJThKO O.LHOpOHOM c1yHKuHH Z = f(x, y)

Z”, c1YHKunn Z = y2 in x paa

x2

2y-

2y

x

Z 4YHKUHH Z = y2 in x paa

y2

y x

y2

x2

x2

Z, 4YHKUHH Z = + — y2 +7 paa

2 1

3x+

1

—2

6x+

flonHsffl W144ePeHLWaJ1 dz 4yHKLU!M Z = x2 in y pae

2xlnydx+

y

x2dx+lnydy 2x

—dxdy

y

2xylnydx—x2dy y

ilpil CI1OB1k[51X B2 — 4AC < 0, A > 0 KB443TMH51 4opMa Ax2 + Bxy + Cy2 5IBI15ITC5I

3HaKOHeOHpe4eneHHOfl

OTPIWTJThHO

HHOI1O)KIE1TJThHO ollpe.ReHeHH0FI

HOI1O)KIE1TJThHO oHpe4eI1eHHoH

ilpil CI1OBIE1IE1 B2 — 4AC> 0 KB443TMH51 4opMa Ax2 + Bxy + Cy2SIBJIaeTCSI

3HaKOHeOHpe4eI1eHHOit

OTP1k1L1TJThHO oHpe,LeneHHoIE1 HHOI1O)KIE1TJThHO oHpe,LeneHHoIE1HOI1O)KIE1TJThHO oHpe,reneHHoF1

11pM)/C.TIOBIkISIX B2 — 4AC = 0, A <0 KB443THH51 4opMa Ax2 + Bxy + Cy2 5IBJ15ITC5I

3HaKOHeOHpe4eI1eHHOit

OTP1k1L1TJThHO

HHOJ1O)KMTJThHO oHpe_reneHHoF1

HOI1O)KMTJThHO

11pM CI1OBH5{X B2 — 4AC = 0, A > 0 KBa,TpaTHHan 4JopMa Ax2 + Bxy + Cy2 5IBJ15ITC5{

3HaKOHeOHpe4eI1eHHOit

HOTF1T4TJThHO OH4WI[HHOF1HHOJ1O)KHTJThHO oHpeLeneHHoF1 HOJ1O)KHTJThHO oHpeLeneHHoF1

KBapaTHHaS 4opMa —4x2 — 3xy + 2y2 flBI15JTC5I

3HaKOHeOHpe4eI1eHHOit

OT1k1T4TJThHO

HeHOJIO)KHTeJThHO oHpeLeneHHoF1

HOTHT4TJThHO

KBapaTHHaS 4opMa —4x2 + 3xy — 2y2 flBI15JTC5I

3HaKOHeOHpe4eI1eHHOli

OTMT4TJThHO

HHOJ1O)KHTJThHO oHpeLeneHHoF1

HOTHT1TJThHO

KBapamHa51 4JopMa 2x2 — 3xy + 5IBI15ITC5I

— 3HaKoHeoHpe.LeI1eHHo11 OTPHUTJThHO oHpeeI1eHHoM

— HOTPHUTJTbHO oHpeeI1eHHoM

— HO.T1OK14TeJmHO oHpe.LeJIeHHo11

KBapamHa51 cjopMa 4x2 — l2xy + 9y2 51BI151TC5I

— 3HaKoHeoHpe.LeI1eHHo11 OTP14UTJThHO oHpeeI1eHHoM

— HOTP14UTJThHO oHpeeI1eHHoM

— HO.T1OKF1TeJmHO oHpe.LeJIeHHoF1

KBapamHa51 cjopMa —9x2 + 24xy — 16y251BJI51TC5I

3HaKoHeoHpe.LeJIeHHoF1

— OTPF1UTJThHO oHpeeI1eHHoM

— HOTPF1UTJThHO oHpeeI[eHHoM

HeHO.nOKF1TeJmHO oHpe.LeJIeHHoH

KBapamHa51 cjopMa x2 — 4xy + 5y2 5{BJ15{TC5{ 3HaKOHeOHpe.LeI1eHHOF1

HeHO.T1OKF1TeJmHO oHpe,LeJIeHHoH HOTP11UTJThHO oHpeeI1eHHoM

HO.T1OKF1TeJmHO oHpe,reJIeHHoH

Z YHKUMM Z = + — y2 +7 paa

—2

x3

6x+—2

6x+ 2

HOJlHbIii WffJ4JepeHUHaI1 c1JYHKUHH Z = y2 in X pae

2xydxdy

—lnxdx +y2dy

YdX + 2ylnxdy

—dxdy

HOI1HbIIi H4J4JepeHUHaI1 c1JYHKUHH Z x3e2 pae

—x2e2”(3dx + 2xdy)xe2(3dx + x2dy)

—x2e2(3dx — 2xdy)x2e2(3dx + 2xYdY)

HOIIHMiI w epeiwai cjyHKLUrn Z = x2 cos 2y pae

— 2x(cos 2ydx — x sin 2ydy)

— x(2 cos 2ydx — x sin 2ydy)

— 2x(cos 2ydx + x sin 2ydy)

x(2 cos 2ydx + x sin 2ydy)

HOI1HMIi.2wcxjepeHLwaJI c1yHKwrn Z = pae

— x(2 cos ydx + x sin ydy) x(2 sin ydx — x cos ydy) x(2 cos ydx — x sin ydy)

— x(2 sin ydx + x cos ydy)

Z 4yHKurnI Z = paa

6x2tgy cos2y

2x2tgy

cos2y 6x2tgy

cos2y 6x2tgy

sin2y

Z 4YHKUMM Z = y2 tg x paa

2y2 cosx

sin3x 2y2 sinx

cos3x

2y2 cosx

—

sin3x 2y2 sinx

—

cos3x

Z 4yHKUMM Z = xsin2y paa

—2xcos2y

—4xsiny

—2x cos 2y 4x cosy

HOJlHbIIi wI4J4JepeHuHaIl 4JYHKUHH Z = in 1Jx2 + y2 pae

—xdx +ydy

x y

xdx+ydy

,Jx2+y2

xdx+ydy

x2+y2

Z dyHKuHH Z = y2tgx paBHa2ysec2x2y secx cosecx—2ysec2xy secx cosecx

Z1, 4yHKwrn Z = x2sin2y paBHa—2x sin 2y2x sin 2y4x sin y4x cosy

TEMA 6. OdiloBilbie TdOdMbI J1I)dPdHhIHJIbHO[O nc’IncJIeHHsI. ilpilMelleilne IIPOII3BOJIHOII JIJI1I IICC.JIeJIOBaHIISI cjyHKu1III

YHKUH5I y=f(x) 11MT B TO’-IKe Xo MaKCHMyM, ec.rw

f’(x0) = O,f”(x0) = 0

f’(x0) = 0, f”(x) <0

f’(x0) >0, f”(x0) <0

YCJIOBHeM BM11KJ1OCT11 KpHBOH yf(x) B F1HTBJ1 (a, b) 5IBJ15ITC5I

f”(x)=O

f”(x)>O

— f’(x)<O

f”(x)<O

YCIIOBHeM BOFHTOCT11 KpHBOH y=f(x) B 11HTdBJ1d (a, b) 5IBII5IdTC5I

— f(x) <0

— f’(x) >0

tyHKuw1 y = f(x) B TO’-we X0 MMddT MMHMMyM, eci

f’(x0) = O,f”(x0) <0

f’(x0)< 0, f”(x0) >0

f’(x0) >0, f”(x0) = 0

f’(x0) = 0,f”(x0) >0

tyHKuH5{ f(x) HMddT B TO’-we X0 MaKCHMyM, dCJT[I I15{ BCex X 113 HeKOTOpO1i OKdCTHOCTH TO’-IKM X0 BMHOJIH5{dTC5{ HdBdHCTBO

f(x0) f(x)

f(x0) 0

f(x0) f(x)

f’(x0) >0

I’yHKuH5{ f(x) HMddT B TO’-We X0 MHHMMyM, eci JI51 Beex X 113 HeKOTOpOii OKCTHOCT11TO’-IKM X0 BM11OJ1H5{TC5{ HBHCTBO

f(x0) f(x)

f(x0) 0

—f’(x0)<0

f(x0) f(x)

Ec.TIH c1JyHKUH5I y=f(x) BO BHTHHH TOK X0 o6IlacTn oHpe,LeJ1eHwI,LwxepeHunpyeMa H OCTHFT B TOK X0 Hall6oJmmero H HHMHMJIFO 3HaqeHH5I, TO HpOH3BO,LHa5I YHKUHH B 3T011 TOK

f’(x0) 0

— f’(x0) He CYLUCTBYT

f’(x0) =

KpHTHTIeCKHMH TOT-IKaMH c1yHKuHHf(x) Ha 3KcTpeMyM, H3MB}OTC5I TOqKH, B KOTOMX JT5J c1YHKTWHf(X) BMHOI1H51TC5J CJIOBH

Дата добавления: 2015-10-30