
apairiema OCH opLHHaT
OCH a6cUHcc OCH a6cUHcc
113 TeOpeMlil JIaHFpaH)Ka cJ1eyeT, TO B HHTBJI (a;b) HaHeTc5I TOqKa C TaKa5I, qTo
f(b) - f(a) b—a
 f(b)+f(a)
f(b)+f(a)
b—a
f(b) - f(a)
b+a
= f’(c)
- f()
= f’(c)
K 4JyHKUH5{MJ(x) H g(x) eopea KOIIIH HpHMeHHMa, ecylH
f(x) H g(x) Ha (a;b) H LHcxjepeHuHpyeMbI Ha (a;b)
—f(x) H g(x) HCHCh[BHh[ Ha [a;b] H g’(x) 0 B HHTCBI1C (a;b)
f(x) H g(x) HCHCh[BHM a [a; b], Hc1xepeHuHpyeMM Ha (a;b) H g’(x) 0 B HHTCBI1C
(ab)
f(x) H g(x) HCHCbIBHh[ Ha (a;b), Hc1xepeHuHpyeMM Ha (a;b) H g’(x) 0 B HHTCBI1C
(ab)
Ecirn 4JyHKUIWJ(x) Fi g(x) HIIEIBHM Ha OT3K [a; b], .LwjxjepeHuMpyeMbI B (a;b) 11
g’(x) 0 B HHTBI1 (a;b), To, corllacHo TeopeMe KomH, B HHTBJT (a;b) HaMeTc5I TO’-IKa
C TaKa5l, qTO
f(b) - f(a)
f’(c)
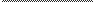
 -
-
g(b) — g(a) g’(c)
f(b) + f(a)
f’(c)

 -
-
g(b) + g(a) g’(c)
f(b) - f(a)
f(c)

 -
-
g(b)—g(a) g(c)
f(b) - f(a)
g’(c)

 =
=
g(b) — g(a) f’(c)
HpaBFLTIO JTOHFITa.T151 HF1MH51TC51 K HeOHpe.LeJ1eHHOCTF1 BHLa
—O.cD
| HpaBIfflOJIOHFITa.T151 HF1MH51TC51 K HeOIIpeLeJ1eHHOCTH BHLa | ||
| —O.cc | ||
c/D-c/D
HyCm cl?yHKWWJ(x) H g(x) HHMBHM B (x0,a],,LwxepeHuHpyeMbI B (x0,a),HpHT-IeM
|
i—n0
f’(x)
 urn TO
urn TO
X+X0 g’(x)
u • rn
f(x)
-
-
hrn
f”(x)
x—>x0 g(x) x—>x0 g (x)
• f(x)
f’(x)
=
g(x) g’(x)
u • rn
x—>x0
f(x)
g(x)
f(x)
|
x—>x0
f’(x) g (x)
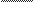 urn
urn
x—>x0 g(x)
= const
HyCTb 4yHKUHHJ(x) Fi g(x) HHhIBHhI B (x0,a],,LwxepeHLuipyeMbI B (x0,a),npne
g’(x) 0, Tim f(x) =0 Fi lirng(x) =0; CYCTBYT KOHeHM1I 111111 6ecKoHeHbIi pee
X—*xo x—*xo
urn
f’(x)
TO
X>X0 g’(x)
h • m
f(x)
|
f’(x)
x—>x0 g(x) x—>x0 g (x)
|
|
f’(x)
x—>x0 g(x) g (x)
T • im
f(x)
—c
x—>x0 g(x)
u • rn
f(x)
-
-
urn
f”(x)
x—>x0 g(x) x—>x0 g (x)
HpHMeHHMa iiii ‘reopervia PoJu15I K YHKUHH f(x) = 2 + /(x _1)2 Ha oTpe3Ke[1;2]HeT, y=f(x) 3MBH Ha OT3K [1;2]
— a, c=1
HeT, y=f(x) He,THc1X1ePeHUHPYeMa B HHTBJ1 (1;2)
HeT, f(1) f(2)
HpHMeHHMa IIH eopea JlarpaH)Ka K 4YHKUHH f(x) = + 2x +1 Ha OT3K [0;2]
HeT, d2yHKUH5IJ(x) 3MBH Ha [0;2]
HHMHHM
— HeT, cIyHKuH51J(x) He.LH4xepeHuHpyeMa B (0;2)
HeT, f(0) f(2)
HpHMeHHMa IIH eopea KOIIIH K 4YHKU1151M f(x) = 2x +3 H g(x) = Jx —1 Ha OT3K [0;2]15
c=———
HeT, f(0) f(2)
HeT, 4YHKUH5 g(x) He opeeiiea HH x e [o;1)
HeT, 4JyHKUH5{ g(x) HeHc1c1epeHuHpyeMa Ha (0;2)
ECIIH 1JYHKUH5I y=fx). LHc1Jc1JepeHuHpyeMa B HHTBI1 (a;b), TO JI51 Bo3pacTaHH5{f(x,) B (“a;b,)
Heo6xoHMo H)ocTaToqHo, TO6bI)I151 Bcex x e (a; b) BMHOJIH5IJIOCb
f’(x) >0
f’(x) =0
f’(x) <0
—f”(x) O
ECIIH 4YHKUH5I y=f(x,),rHc1Jc1JepeHuHpyeMa B HHTBJI (‘a;b,), TO JI51 y6bIBaHwlf(x,) B (“a;b,)
Heo6xoHMo H)ocTaToqHo, TO6M)I15I Bcex x e (a; b) BBIHOJIH5LJIOCb
f’(x) >0
f’(x) =0
—f”(x) O
f’(x) <0
aa c1yHKuw1 f(x) = 2x4 + x3 +1, Tor,La
x=O 51BI151TC51 TOT-1K011 MHHHMM cyHKuHHf(x)
X = —— 51BI151TC51 TOT-IKOH MHHHMM c1yHKuHHf(x)
c1yHKuHHf(x) He HMT 3KCTMMOB
X = —— 51BI151TC51 TOT-IKOH MKCHMM 4yHKuHHf(x)
YHKUH51 f(x) = — 4xBO3CTT Ha (— co;+co)
BO3CTT Ha (—2:2)
BO3CTT Ha (— co—2) u (2;+co)
BO3CTT Ha [—1 2]
YHKUH51 f(x) =
— 4x
y6bIBaeT Ha (—2:2)
—
y6MBaeT Ha (— c+c)
y6bIBaeT Ha [—a2)
y6bIBaeT Ha (— c—2) u (2;+c)
YHKUH51 f(x) = 2Vx —3 BbIHKI1 Ha HHTBI1 (—c.c;3) BOFHT Ha HHTBJ1 (3;+c.c)BMHKJ1 Ha HHTBJ1 (3;+c.c)
BOFHT Ha HHTBJ1 (3;5)
HyCTb 4JYHKUH5I y=f(x) B (a;b), x0 — BHTHH5{5{ TOK 3T0F0 HOM)KTK H
f’(x0) = 0 (HIm f’(x0) He cywecTByeT), TO
— o63aTeJmHo TOqKa MHHHMM
— o63aTeJmHo TOqKa MKCHMM
— o6M3aTeIlbHo TOqKa HeperH6a
B TOK X0 3KCTMM MO)KT cyluecTBoBam, a MO)KT H He CYWCTBOBTh
K cl?yHKUHH y=f(x) Ha OT3K [a; b] eopea PoJu15I HpHMeHHMa, ecirn
—f(x) Ha [a;b],. Lw1x1epeHuHpyeMa B (a;b) Hf(a)f(b)
—f(x) Ha [a;b]Hf(a)=f(b)
—f(x) w1J4JePeHuMpYeMa B (a;b)
—f(x) B (a;b),,LW1X1?ePeHUHPYeMa B (a;b) Mf(a)f(b)
113 TOMM JIarpaiDRa cJ1eyeT, qTo
rno6a5l K yHKUHHf(x) B (a;b) apauiema xop,Le, CT5JFHBa}omeHKOHLUil yrHf(x) Ha OTpe3Ke [a;b]
K yHKuHHf(x) B (a;b) apauieiia rno6oIi xop,Le B DTOM
HHTBI1
xopa, CT5JFHBIOW5I KOHU )iyrHf(x) a [a; b], napaeiia OCH OY
B FIHTBI1 (a,b) HaMeTc51 KaCaTeJThHa5I, napa.riileJmHa5I xope, CT5JFHBaIOWeH KOHLIbI
yrFIf(x) Ha OTpe3Ke [a; b]
EcjmToqKa x0 51BI15JTC5J TO’-1K011 HeperH6a rpaHKaf(x) C BepTHKaJmHOH KaCaTeJThHOH, TO
f (x)=O
f’(x0) =
f’(x0) =0 H f”(x0) =0
ECJ1M TOT-wa 5IBJI5JeTC5J TO’-IKOH HeperH6a rpacrnKaf(x) c HaKJIOHHOH KaCaTeJmHOH, TO
f(x0)=0M f(x0)=0
T0-wa x0 H3MBTC5J TO’-IKOH Heperll6a rpa4HKaf(x) C ropw3oHTaJmHoH KacaTeJmHoH, eCJIH
f’(x0) =0 H f”(x0) =0
f (x)=O
HpMMeHHMa JIll eopea Poiiiii K 4YHKLIHH f(x) = 3 + J2 — X Ha OT3K [0;2]
a, c=2
HeT, cl?yHKUH5{f(x) He oHpeLeI1eHa HH x e [0;2] HeT, 4JYHKUH5If(X) He Hc1c1epeHuHpYeMa B (0;2) HeT, f(0) f(2)
ilpilMellilMa 1111 eopea JlarpawKa K 4JyHKUHH f(x) = 2— Ji + X Ha OT3K [—1;0]
HeT, c1JyHKuH5{f(x) pa3pbIBHa Ha [—1;0]
HHMHHM
HeT, c1JyHKuH5If(x) He Hc1xepeHuHpYeMa B
(—1;O)
HeT, f(-1) f(0)
TOKaMH HeperFl6a c1yHKLwH y = — 6x2 5JBJI5JIOTC5J
— TOKH = 2J — 2J
— TOJThKO TOK xO
— TOT-IKH = —2 Fi = 2
— y 4yHKwW y = — 6x2 HT TOT-IeK HeperH6a
HpHMeHHMa iwi eopea KOhl K YHKUH51M f(x) = 2x +1 Fi g(x) = —2 Ha OT3K [0;3]
HeT, 4JyHKUWI g(x) He.1rnc1x1epeHuHpyeMa B (0;3) H g’(x) = 0 B (0;3)
— a, c=3
HeT, c1yHKuH51 g(x) 3MBH Ha [0;3]
HeT, g(x) He Hc1x1ePeHuHpYeMa B (0;3)
YHKUH y = — HMT TOK HeperH6a C FOH3OHTbHO B TOK
(2;—2)
—(O;—3)
—(O;O)
Ho HBHJ1 JIOHHTaJI5{ Hpe.LeI[ hn
—0
5
1—cos3x
5x2
Pae
YHKUH5I y = + 2x BO3CTT TOJThKO HH
x (0;+cc)
xE(—3;2)
x (—ci+ci)
x e (—oc;0)
KpHBa y = + 3x2 —5 BOFHT HH
x e (—co;+co)
xel —c’—— lul —;+ci
3) 3
xel —-——;-——
YHKUM5I y = — x y6bIBaeT llH
xe(—1;1)
— x e (—1;O) u (O;1)
x e (—co;—1) u (1;+co)
— xe(—co;O)u(O;+co)
ilpil 111111
O)
Tim (f (x)- g(x)) = lim(f’(x)- g’(x))
x—*xo x—*xo

 urn = urn
urn = urn
X—*X g(x) X—*XO g’(x)
urn (1(x). g(x)) = Tim (f’(x).g’(x))
x—*xo x—*xo
urn f(x)
= urn
f’(x)g(x)-f(x)g’(x)
x—*x0 g(x) x—*x0 g2(x)
Ho paiuiy JIOHFITaJI5I 19
e4x_1
 — 5x)
— 5x)
Pae
t’yHKuH5{ y = f(x) H3MBTC5I BO3paCTaIOweII B HHTBJ1 (a; b), ec.iill I151 IlIo6bIx
E (a;b) ii x2 E (a;b)
M3 X1 > x2 ciieye f(x1) < f(x2) M3 X1 <x2 ciieye f(x1)> f(x2) 113 X1 <x2 ciieye f(x1) < f(x2)
113 = x2 ciieye f(x1)> f(x2)
cos3x
 Ho HpaBH.ny JT0HHTa.T151 “v 2x — r pae
Ho HpaBH.ny JT0HHTa.T151 “v 2x — r pae
YHKUW1 y = f(x) H3MBTC51 y6bIBa1oweIi B HHTepBa.lle (a;b), ecrni yii rno6blx x1 e (a;b)
H X2 e (a;b)
113 X1 <x2 ceye f(x1) < f(x2)
113 X1 > x2 ceye f(x1)> f(x2)
113 = x2 ceye f(x1) < f(x2)
113 X1 <x2 ceye f(x1)> f(x2)
 Ho paiuiy J1oHHTaJ151 1
Ho paiuiy J1oHHTaJ151 1
---
ctg2x gx
pae
—1
HpHMeHHMa 1111 eopea Po111151 K 4YHKU1111 f(x) =
—La, TaKKaK f(—2)= f(2)
 x- —1
x- —1
Ha OT3K [— 2;2]
a, aic KK f(x) Ha OT3K [— 2;2] H f(— 2) = f(2)
a, aic KK f(x) Ha OT3K [— 2;2], H4xepeHuHpyeMa B (— 2;2) H
f(—2)= f(2)
HeT, He BMHOJ1H51TC51 CI1OBH H11MBHOCTH
A6cUHccbI TO’-IeK HeperH6a 4YHKUHH f(x) = 2x4 — 4x2 +3 BHbI
±1HO
 1
1
HpHMeHHMa JIM eopea JTarpawKa K YHKUHH f(x) = Ha OT3K [— 1;1]
— HeT, 4JYHKUH5I He.LH4X1ePeHUHPYeMa B (— 1;1)
a, TK KK f(— 1) = f(1)
a, 4YHKUH5J Ha [— 11] H f(— 1) = f(1)
a, 4JYHKUH5I Ha [— 11],.LHc1x1ePeHuHpYeMa B (— 11) H f(— 1) = f(1)
YCJIOBHe f’(x0) = 0, f”(x) < 0 51BJ15JTC5J CJIOBHMMHHHMM
BOFHTOCTH
MKCHMM
y6bIBaHwJ
YCJIOBHe f’(x0) = 0, f”(x0)> 0 51BJ15JTC5J CJIOBHMMKCHMM
BMHyK.LIOCTH
BO3CTHH51 MHHHMM
TEMA 7. fipilMeHeHile JUIijHjepeHHHaJ1bHO[O HC’IHCJIeHHH B 3KOHOMWICKHX
IICCJIOBHHHX
‘IyHKuM51J(x) B F1HTBJ1 (a, b) y6bIBaeT Bce 6blcTpee, eciTH
f’(x)<O,f”(x)<O
f’(x)<O,f”(x)>O
f’(x)<O,f(x)>O
f’(x)<O,f(x)<O
tyHKuH51J(x) B F1HTBJ1 (a, b) BO3CTT Bce MeJTeHHee, eciTH
f’(x)>O,f”(x)>O
f(x) > O,f’(x) >0
f’(x)>O,f”(x)<O
f(x)<0,f’(x)>O
3.TIaCTHqHOCTb cl?YHKUIW y =J(x) oHpe.LeI15JeTc5I no 4opMyYIe
E(y)=Ly’
E(y)=
X
 y.y
y.y
y x y
4T06M 4JyHKUW{ y =J(x) 6MIla 3JIaCTHqHOH B TOT-lKe, HOK3TJTh 3JTCTHHOCTH OJDKH 6bIm
6omme HJ15J
MeHJ3me)HHHUM
pae eHHHUe
6oimme eLHHHuM
4To6Jil 4JyHKUH5{ y =J(x) 6MIla He3JIaCTHqHOH B TOK, HoKa3aTeJm 3J1CTHHOCTH LoJDKeH
6Mm
MeHJ3Lue HJ15{
MeHJ3me eLHHHuM 6oimme eLHHHuM pae elwHHue
3.TIaCTHqHOCTh 4YHKUHH 3KOHOMHCKH oaae
OTHOCHTJThHO W3MHHF1 apryea upil OTHOCHTJThHOM W3MHHHH cIYHKLu1H OTHOCHTJThHO W3MHHF1 cIYHKUHH Ha 1% HPH OTHOCHTJThHOM H3MHHHH apryea OTHOCHTJThHO H3MHHH cIYHKUHH HH OTHOCHTJThHOM H3MHHHH apryea OTHOCHTJThHO H3MHHH cIYHKUHH HH OTHOCHTJThHOM H3MHHHH Ha 1%
3.TIaCTHqHOCTh HpOw3Be.LeHH51,LByX cyHKuHn E (uv) paa
— vE(u)+u.E(v)
E(u).E(v)
E(u)+E(v)
— E(u)+E,(v)
3JTaCTHHOCTb CTHOFO BX cyHKuHi E paa
E(u)
E(v)
E(v)
E(u) E,(u)—E(v)
E(u)—E(v)
41115{ HOIly’-IeHH5I MaKCHMaJmHOH HpH6bLrIH Heo6xoLHMo, TO6M HH LaHHOM O6EeMe HOH3BOCTB xo
BMpy’1Ka 6buIa 6oimme rIpeLeJmHbIx u3Lep)KeK
BMpy’1Ka 6MIla MHMJI peeimix H3Lep)KeK
BM1K BH5LTICb npeeJmHMM H3Lep)KKaM
BMpy’1Ka 6buIa HaH6oJmmeH
tyHKuH5I y = f(x) B HHTBJ1 (a;b) Bo3pacTaeT, ecw
f’(x) <0
f’(x)>O
f”(x)>O
f”(x) <0
YHKUH5I y = f(x) B HHTBJ1 (a;b) y6MBaeT, eciiii
f’(x) >0
f’(x)<O
f(x) >0
YHKUM51 y = f(x) B F1HTBI1 (a;b) BO3CTT Bce 6iic’rpee, ec.riH
f’(x)>O,f”(x)<O
f’(x)>O,f”(x)>O
f(x)>O,f’(x)>O
f’(x)>O,f”(x)=O
tyHKuw1 y = f(x) B F1HTBI1 (a, b) y6bIBaeT Bce eeee
f’(x)<O,f”(x)>O
f’(x) < O,f”(x) <0
f(x)<O,f’(x)<O
f(x)>O,f’(x)<O
3iiacmHocm cpoca S(p) OTHOCF1TJThHO UeHJil p no opyiie
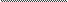 p
p
p SS’(p)
 E p
E p
Eciin K(x) — HoIlHJ3Ie H3,LepKKH, TO npeeme H3)KKH oHpeLeJ15noTc5I KK
—K’(x)
lirnK(x)
x—*xo
urn K(x)
fK(x)dx
3JIaCTWIHOCTb HOCTO5IHHOH BJ1HHHM paa HOCTO5IHHOFI einne
HJI[O
ewnue
BM
4II[5{ HoJ1y1-IeHH5I MaKCHMaJmHOH HpH6bIIlH LOcTaTOqHO, TO6bI ilpil LaHHoM o6eMe HOH3BOCTB xo
V”(x0) = K”(x0)
V”(x0) > K”(x0)
V”(x0) <K”(x0)
3KOHOMHecK14 O6yCIIOBJIeHHOM o6iiacmio onpe,LeYIeHwJ YHKUHH HOJIHMX H3)KK K(x)
51BI151TC51
X 0
x 0
Jx 0,
[K(x) 0
Jx 0,
K(x) > 0
YHKUM51 HOIIHMX H3,Lep)KeK K(x) B FIHTepBaJIe (a;b) Bo3pacTaeT, ecii
K’(x) <0
— K”(x) > 0
— K”(x) <0
—K’(x)>O
tYHKUM51 HOJIHOFI BMpyT-IKFI V(x) y6MBaeT B HHTBJI (a;b), ec.r1H
V”(x) >0
V”(x) <0
V’(x)<O
V’(x) =0
iYHKUM51 HOJIHMX H3Lep)KeK K(x) B HHTBJ1 (a;b) BO3CTT Bee CY1H
K’(x) > 0,K”(x) > 0
K(x) > 0,K’(x) >0
— K(x) = 0,K’(x) >0
K’(x) > 0,K”(x) <0
tYHKUH5I HOJIHMX H3)KK K(x) B HHTBI1 (a;b) BO3CTT Bce 6iic’rpee, eciu
K’(x) > 0,K”(x) = 0
K’(x) > 0,K(x) >0
— K’(x) > 0,K”(x) >0
K’(x) > 0,K”(x) <0
HoJlHa5I Bh[4K V(x) ripi x0 6yeT MaKCHMaJmH0H, ecii
V(x0) = 0,V’(x0) <0
V’(x0) = 0,V”(x0) >0
V’(x0) = 0,V”(x0) = 0
V’(x0) = 0,V”(x0) <0
Cilpoc S(p) 6yeT 3I1CTF1HMM HM uee p0, ecni noKa3aTeJm 3J1CTHHOCTFT
6oimme HI15J
MHMJ1 MHMUM
6oimme e.LF1HIrnM
pae e.LnHIrnM
Cilpoc S(p) 6yeT He3IIaCTW-IHMM HM uee p0, ecw llOK3TJTh 3JIaCTW-IHOCTH
— MHMJ1 HJ15J
— 6omme e,LHHF1uM
— MHMJ1 MHHUM
— pae e.Lrnwue
3.TIaCTWIHOCTb c1yHKurn1 cpoca S(p) = 4— p OTHOCF1TJThHO UHM p oHpe,Le.]iIeTc51 KK
 4
4
4-p
 p 4-p 1
p 4-p 1
4-p
 4-p p
4-p p
3JIaCTWIHOCTMO cI?yHKLurnf(x) OTHOCF1TJThHO apryea X H3MBTC5I peeii OTHOCF1TJThHOFO HPHPWHH5{ 4YHKuHH HH AX —* 0
peeii OTHOTJIHH5{ OTHOCHTJThHOFO npHpaeHH5{ apryMeHTa K OTHOCIITJJbHOM
ppawerno cl?yHKUHH HH AX —* 0
HpeeI1 cl?yHKUHH HH AX —* 0
peeii OTHOTJIHH5{ OTHOCHTJThHOFO npHpaweHH5{ 4yHKUHH K OTHOCHTJTbHOM
HpFlpaweHHIo apryea HH AX —* 0
3KoHoMF1ecK11 O6yCJlOBneHHOH o6iiacmio YI51 4yHKLiHH cupoca S(p) = 8— 2p 6yeT
P O
p 4
p 4
—O p 4
Cpeiwlle H3Lep)KKH (x) HH X0 6yyT MHHHMaJmHbI, CJTI4
—K(x0)<O
K(x0) = O,K(x0) <0
K(x0) = O,K(x0) >0
HoJTHa5l BMpy’lKa V(p) B F1HTBI1 (a;b) BopacTaeT Bce ec.rrn
V’(p) > 0,V(p) <0
— V’(p) > 0,V(p) = 0
V’(p) > 0,V”(p) <0
V’(p) > 0,V”(p) >0
Ho.nHa5l BbIpyT-IKa V(p) B F1HTBJ1 (a;b) y6MBaeT Bce 6blcTpee, ecii
— V’(p) <0,V(p) >0
V’(p) <0,V”(p) <0
V’(p) <0,V”(p) >0
— V’(p) <0,V(p) = 0
3KOHOMHTIeCKH O6yCIIOBI[eHHOI1 o6iiacmio,LITI5I YHKUHH HOIIHOcI BMKH V(p) = l2p — p2
6yeT
(—co;+co)
— (0;+co)
[0;12]
(12;+co)
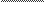 3I1aCTMHOCTb cl?yHKurn1 cpoca S(p) = OTHOCF1TJThHO UeHJil p KK
3I1aCTMHOCTb cl?yHKurn1 cpoca S(p) = OTHOCF1TJThHO UeHJil p KK
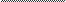 p
p
p (p+2)3
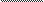 E(S)= p
E(S)= p
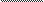 p p+2
p p+2
E (S)=
 (p+2)2
(p+2)2
HoKa3aTeJm 3J1CTHHOCTII 4YHKUHM y = + X HH X = 1 pae
HoKa3aTeJm 3JICTHHOCTII c1JYHKUHH y = —2 ripi x = 2 pae
—36
HoKa3aTeJm 3J1CTWIHOCTH cpoca S = 8— 2p ripi uee p = 3 pae
HoKa3aTeJm 3.TIaCTFIqHOCTI1 4YHKLUW y = in(x2 + i) HH x=1 pae
in 2
in 2 in 2 2
21n2
Cilpoc 5(p) = 6— p OTHOCF1TJThHO UHM p 6y,LeT 3JIaCTHT-IHMM 11H
p e (3;+)
pe(O;3)
p e (3;6)
p e (— 3)
HoJlHa5 Bipy’-iKa V(p) HH 3HHOM cpoce S(p) = 16— 2p 6yeT HaH6oJmmeH llH uee p, BHOF1
Cilpoc S(p) =8—p OTHOCHTJThHO LeHbIp 6y,LeT H3J1CTHHMM HH
pe(4;8)
p e (O;4)
p (4;+c)
p E (— 4)
HoKa3aTeJm 3I1CTHHOCTH HOI[HOI BMKH V(p) HH 3HHOM cpoce S(p) = 16— 4p HH
uee p = 1 pae
tYHKUM51 HOJIHMX H3,Lep)KeK K(x) = 2x3 — 24x2 + lOOx + 36, r,ie x — o6’beM npow3Bo,LcTBa,
Bo3pacTaeT Bce eiieee B HHTBJ1
(4;+)
(0;4)
(-4)
(0;+co)
Hornible M3KH K(x) = — 6x + 39x +13, re x — o6eM npoH3BocTBa, BO3CT}OT Bce6blcTpee B HHTBJ1
(0;6)
(-6)
(6;+)
(—+)
Ho.nHble H3))KKH K(x) = 2x3 — 24x2 + 120x + 40, re x — o6eM npoH3BocTBa, BO3CT}OT Bce 6iic’rpee B HHTBJ1
1(4;+c/D)
(0;4)
(-4)
(0;+cID)
Cilpoc S(p) = 24— 4.p OTHOCHTJThHO UeHJil p 6yeT H3J1CTHHMM HH
p e (3;6)
p e (3;+)
p e (0;3)
p e (— 3)
x
 HoKa3aTeJm 3J1CTHHOCTH c1JYHKUHH y = HH x = 2 pae
HoKa3aTeJm 3J1CTHHOCTH c1JYHKUHH y = HH x = 2 pae
x +9
5
x
Ecirn HOI1HbI M3,LepKKM H BMpyT-lKa COOTBTCTBHHO COCTBJ15I}OT K(x) = — 3x + 12x + 20;
V(x) = — 4x2 + 22x +11, TO llpH6bIIIb Z(x) 6y.LeT MaKCHMaJmHOIi npn O6TeMe HOH3BOCTB X, paBHOM
YBeirneHHe B cpoce llH IIOCTO5JHHOM 11pe,LO)KeHHH yMeHbmaeT BHOBCHIO i1ey
yBe.T1w-IHBaeT BHOBCHIO uey
yMeHbmaeT BHOBCHO KOrnP-IeCTBO oapacoxpaH5leT BHOBCHO KOI1HCTBO oapa
YMeHMJIeHHe B cpoce HH IIOCTO5IHHOM IIJIO)KHHH
yBeJIHqHBaeT BHOBCHIO uey
yBe.nw-IHBaeT BHOBCHO KOJThqCTBO oapayMeHbmaeT BHOBCHIO uey
coxpaH5leT BHOBCHO KOI1HCTBO oapa
YMeHMJIeHHe B HI1O)KHHH HH IIOCTO5IHHOM cupoce
yBeJ1w-IHBaeT BHOBCHIO uey
yBeJIw-IHBaeT BHOBCHO KOI1HqCTBO oapa
yMeHJ7maeT BHOBCHIO uey
coxpaH5{eT BHOBCHO KOI1HqCTBO oapa
YBe.nwIeHHe B HI1O)KHHH HH HOCTO5{HHOM dilpOCe
coxpaH5leT BHOBCHO KOJ1HCTBO oapayBeJIw-IHBaeT BHOBCHIO uey
yMeHJ7uIaeT BHOBCHO KOJ1HCTBO oapa
yMeHJ7uIaeT BHOBCHIO uey
KpHBa 3HreI15I HJU1IOCTHT 3BHCHMOCTB eiciy
UHOH oapa H CHOCOM
ueHoH oapa Fi
H)KHMM LOXO,TOM H KOJ1HCTBOM rlpHo6peTeHHoro oapa 3TTMH H 06’beMOM BbrnyCKaeMOH HPO,TYKUHH
C IIOBMTJIHHM BHOBCHOFI UHM p0
dilpoc Fl BJ1WIHBIOTC5I
dilpoc yBeIrnHBaeTc5J, a MHMJJTC5J
— dilpoc Fl MHMJI}OTC5I
cripoc a BJTHIHBdTC5J
C CHIUKHMM paBHOBeCHOH UHM p0
dilpoc yMeHbTJIaeTC5I, a BdJTH4HBdTC5J
dilpoc Fl llpe,LJ1O)KeHHe MHbIIIIOTC5I
clipoc yBeJ1FlFlBaeTc5J, a npeoee M}fbfflTC5J dilpoc Fl BJWHBIOTC5I
TEMA 8. HeonpeIe.J1eHHbIe IIHT[JIbI
‘DyHKUW{ F(x) 5IBI15ITC5J nepBoo6pa3HoFT,1i5I yHKuHHJ(x) B HKOTOOM npoMe)KyTKe, ecw B
rno6oIi TO’-IKe 3T0F0 HOM)KTK BMHOJ1H5ITC5I
— f’(x) = F’(x) F(x)J(x)dx
F’(x)J(X)
dF(x)J(x)
Ecm J f(x)dx = F(x) + C, TO BM11OJ1H51TC5I
F(x)f’(x)
F(x)=f(x)dx d(F(x)+C)=f(x)dx
F’(x) = f’(x)
IdF(x)paBeH
f’(x)
—J(x)+C
F(x)+C
J(x)
Ec.LIM HeoHpeeI[eHHMii HHTerpaJl HMT BHL f f(x)dx, TO,Lw1xepeHuHaJ1 3T0F0 erpaiia
Pae
F(x)dx
f’(x)
f’(x)dx
—J(x)dx
HpOM3BOHa5 OT HeoHpeLeI1eHHoro erpaiia $ f(x)dx paBHa
F(x)
— F(x)+C
J(x)
f’(x)
HHTeFpHpOBaHHe HO ‘-IaCT5{M B HeOHpeLeI1eHHbIX erpaiiax BMHOJTH5ITC5I HO 4JopMyIle
uv—$vdu uv+$vdu uv—$udv uv+$udv
BbI6epHTe epoe yTBep)IcLeHHe
$ uvdx = $ udx $ vdx
$uvdx = $udx+ $vdx
$uv’dx = uv —$vdu
u  fudx
fudx
v fvdx
HHTeFpaJI kf(x)dx pae
k+f(x)dx kf(x)dx k2f(x)dx k-$f(x)dx
HHTeFpaJI j (f(x) + p(x))cb paBeH
f(x)q(x)dx - f(x)
$f(x)ç(x) - $ço(x)dx
— ff(x)dx+$ço(x)dx
$f(x)dxf(x)dx
BbI6epMTe HBF1JThHO YTBP)KLHH
dx 3
 =—x3+c
=—x3+c
 $ dx —3x3
$ dx —3x3
$ dx

 = 3x +
= 3x +
BbI6epHTe HBHJThHO
$dx=
 1
1
5[J
$dx=+c
$dx=+c
5
HeHpepbIBHa YHKUH5I HMT
TOJThKO OH HepBoo6pa3Hylo 6ecKoHeHoe MHOKeCTBO HepBoo6pa3HMx
Be HepBoo6pa3HbIx
KOHHO ‘111db HepBoo6pa3HhIx
Be a3IEWIHbI nepBoo6pa3}mIe O,LHOH H TOll)Ke YHKUHH
BHM M){L C06011 OT.TIHqaIOTC5I Ha KOHCTHT
— OThH’11OTC51 Ha HeKOTOp1O 4JYHKUHIO
— OThH’11OTC51 Ha HHTdFHOBHH5I
Hc1x1epeHuHaJ1 OT HeoHpe,LeIIeHHoro erpaiia pae
BbI)KdHH1O
HOwJHTeFpaJmHOFI c1yHKuHH
HJI[O
— 6ecKoHe’1Hocm
K c1YHKUH5JM OTHOC5ITC5I Bce BO3PCT1OLUH
HMBHM
HHOCTO51HHM cl?YHKUHH
r dx
HHTeFpaJI j pae
2x+1
 1 (2x+1) 2+c
1 (2x+1) 2+c
121n2x+1+C
1n2x+1+C
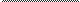 +c
+c
2(2x+1)2
HHTerpaIl $tgxdx pae
—1ncosx+C 1nsinx+C
—1nsinx+C
 tg
tg
|
 HHTerpaIl 2—3x
HHTerpaIl 2—3x
pae
1n2—3x+C
13n2—3x+C
! 3 3x+C
 +c
+c
(2—3x)2
HHTerpa.ri ctgxdx pae
—incosx+C
—1nsinx+C
 ctg
ctg
1nsinx+C
HHTerpai[
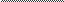 S(2_x)2
S(2_x)2
pae
 +c
+c
2—x
 +c
+c
x—2
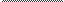 +c
+c
2(2—x)
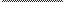 +c
+c
2(x—2)
|
 HHTerpaIl pae
HHTerpaIl pae
q(x)
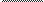 (x) q’(x)
(x) q’(x)
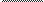 q(x)
q(x)
1n(x)+C
|
 HHTerpaIl pae
HHTerpaIl pae
x
in x +c
x
in2 x+C
1n1nx+C
—in2 x+ C
HHTerpa.r1 $e3x_2dx
ie32 + C
e3X_2 + C
_ie32 +C
1e3x + C
|
 HHTeFpaJI 2 2 pae
HHTeFpaJI 2 2 pae
a+x
arcsin—+C
a
—arcsin—+C
a a
1 x
—arctg—+C
a a
x
arctg—+C
a
HHTerpa.n
dx
 i,ja2 —x2
i,ja2 —x2
pae
—arcsin-- + C
a a
—--arcsin--+C
a a
1 x
—arctg—+C
a a
arcsin— + C
a
HHTerpaI[ $ (K + f(x))dx pae
$f(x)dx K+$f(x)dx i+$f(x)dx
1(x)dx
|
 HHTerpaJl pae
HHTerpaJl pae
1+x2
iarctg2x+C
arctgx + Carctg2x+C 2arctg2x+C
r dx
HHTerpa.r1 I
‘
1+c
in x
 1 +C
1 +C
in2 x
xlnx
pae
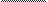 1 +C
1 +C
21n2x
1n1nx+C
HHTerpaJI $cos3xdx pae
1.
—sin 3x + C
sin3x + C1 2
——cos 3x+C
3sin3x + C
HHTerpaJl $ ctg2xdx pae
1nsin2x+C
12insin2x+C
—211nsin2x+C 21nsin2x+C
HHTeFpaJI
rdx
 j
j
pae
lna—x+
—1na—x+C
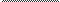 1 +c
1 +c
|
 1 +c
1 +c
2(a—x)2
r dx
HHTeFpaJT j pae
1nx-a+C
 (x — a)2
(x — a)2
—1nx—a+C
 1 +c
1 +c
2(x—a) 2
xdx
 HHTeFpaJI J 2 pae
HHTeFpaJI J 2 pae
x+4
ln(x2+4)+C
 1 +c
1 +c
(x2 4)2
iln(x2+4)+C
lnx+— +C
x
Ec.nM F’(x) = f(x), TO HHTFIIOM $ f(x)dx H3MBTC5I COBOKHHOCTb4yHKuMM BM
f(x)+C
F(x)+C F’(x)+C
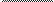 HHTerpaIl $cos2dx pae COS —
HHTerpaIl $cos2dx pae COS —
2 3x
——COS
3 2
—(x + sinx)+ C
1(x—sinx)+C 2
HHTerpaJi $tg2xdx pae
— tgx—x+C
—ctgx—x+C
 3
3
ctg2x+C
HHTerpaJl $e’ cosxdx pae
— ecosxsinx+C
— — e’’ + C
+ C
esmflxsinx+C
HHTeFpaJT f edx pae
1 -3x
--e +C
-e —3x +C
e3x + C
3e_3x + C
HHTerpaJl $ sin2 xdx pae
+ sin 2x) + C
—(x——sin2x)+C 2 2
sin3 x +C
cos x +c
HHTerpaIl $
xdx
 2
2
pae
 2(4—x2)2
2(4—x2)2
1n4_x2+C
_1n4_x2+C 21n4_x2+C
2x +3
HHTeFpaJT $ 2 dx pae
x +3x+5
1nx2 + 3x + 5+ C
I1x2+3x+5+c
1nx +3x+5+x+C
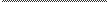 +C
+C
2(x2 +3x+5)2
dx
 HHTeFpaJI $ pae
HHTeFpaJI $ pae
tgx
1ntgx+C
ctgx+C
—1nsinx+C
1nsinx+C
dx
 HHTeFpaJI $ pae
HHTeFpaJI $ pae
ctgx
1nctgx + Ctgx+C
—1ncosx+C 1ncosx+C
dx
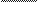 HHTeFpaJI $ 2
HHTeFpaJI $ 2
tgx
tgx—x+C
—ctgx—x+C
 1
1
tgx
—tgx—x+C
 HHTeFpaJI $ dx pae
HHTeFpaJI $ dx pae
(3x —2)
 1
1
2(3x—2)
1n3x—23 +C
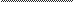 1
1
6(3x — 2)
 1 +c
1 +c
12(3x — 2)
HHTeFpaJT $
dx
 / 4x
/ 4x
pae
J5 — 4x +c
iln(5—4x)+C 2
 1 +c
1 +c
6-J(5 — 4x)3
25—4x+C
|
 HHTeFpaJT pae
HHTeFpaJT pae
J9-x
arcsin+C
9—x +C
 +c
+c
—9—x +C
HHTeFpaJI f x cos xdx pae
—xsinx+cosx+C xsinx—cosx+C xsinx + cosx + C
—xsinx—cosx+C
TEMA 9. OnpeJe.J1eHHbIe, HeCO6CTBeHHbIe H KTHbI HHT[JIbI
EcIIH 4JYHKUH5I Ha OT3K a < b, H rn H M — COOTBTCTBHHO HHMHbTJJ H HaH6oJmmee 3HHWI Ha OT3K [a; b], TO
rn(b-a)f(x)dxM(b-a)
rn(a-b)f(x)dxM(a-b) in(ba)<ff(x)dx<M(ba) M (b-a)<f(x)dx<m(b-a)
YHKUH51Y = f(x)HHTerpHpyeMa Ha OTpe3Ke [a;b], eCJTII oHa
Ha 3TOM OT3KMOHOTOHH Ha 3TOM OT3KHOTPHUTJThH Ha 3TOM OT3K HO.nOKHTeJmHa Ha 3TOM OT3K
3HaeHHe oHpeeI[eHHoro erpaiia 3BHCHTTOJThKO OT OT3K [a;b]
— TOJThKO OT HOwJHTeFPaJmHOH 4YHKUHH f(x)
OT OT3K HHTFHOBHH5J [a; b] H OT HOwilHTeFPaJmHO 4YHKUHH f(x)
OT dlloco6a BbIHCI1HH5{ opeeiieoro erpaiia
ECILH cl?YHKUH5I f(x) H HOTPHUTJThH Ha [a; b], re a < b, TO 3HHH
oHpeeI[eHHoro HHTerpaiia 6yeT
HO.r1OKHTeJmHJ,IM
HOTPHUTJThHMM OTPHUTJThHMM
rno6bIM
TeopeMa 0 cpee 3HHHH oHpeeI1eHHoro HHTeFpaJla BbInoJm5leTc5{, CJTH YHKUH5I
HMT KOHe’-IHOe ‘-IHCJIO TO’-IeK papia llepBOrO poaOFpaHH’-IeHa Ha OT3K [a; b]
HOTPHUTJThH Ha [a;b]
Ha OT3K [a; b]
Heco6cTBeHHbIi HHTFI1 f(x)dx CXOHTC, eCiiH
Lirn$f(x)dx=ci
a
b
Lim f f(x)dx — KOHHO ‘-111db
b—*ca a
b Limff(x)dx=—czD b—*oo a
b
Limff(x)dx He CYWCTBYT
b—*c a
EC.T1H Fx) — HepBoo6pa3Ha5J K cyHKunnftx) Ha [a,b], TO aene onpe,LeJ1eHHoro HHTeT’pajTa
S f(x)dx BHO
F(a)—F(b)
— F(x)+C
— F(b)—F(a)
— F(x)-C
yHKuH51J(x) Ha OT3K [1;8], Sf(x)dx = 13 H Sf(x)dx = 4. Tora
HHTF If(x)dx pae
—17
HHTeFpaJI f(x)dx pae
2f(a) 2a
ECIIH c1:yHKuH5IJ(X) Ha [a,b], ToJ(x) H H [b, a:i H BM11OJ1H51TC51
Sf(x)dx1f(x)dx ff(x)dx =f f(-x)dx
Sf(x)dxSf(-x)dx
ff(x)dxf(x)dx
Heco6cTBeHHbIIi FIHTeFpaJI ff(x)dx pacxowrc5J, ec.rin
Lim ff(x)dx— KOHHO qHC.T1O
a
b
— Limff(x)dx=
b—*cjD
a
b
— Lim$f(x)dx = 0
a
b
Lim f(x)dx — KOHHO OTF1UTJThHO tWCIlO
a
EcIIM cjHrypa o6pa3yeTc5l KHBMMH y = f (x) Fi y = f2 (x) Fl Ha OT3K [a,b], r,ie a = H b = x2 (x1 <x2) — a6cUHccbl TO’-IeK epeceewi,LByX KpnBbIx, f2 (x) f (x), TO HJ1O,Lb 3TOFI cFHrypM oHpe,LeJI5IeTc5I HO copyie
b
S = f(f2(x)-f1(x))dx
S=f(f2(x)+f1(x))dx
S = [(f1(x)f2(x))dx
S = f(f1(x)-f2(x))dx
OHpeeI[eHHMii HHTFJ1 HO T-IaCT5IM BMHCJ15{TC5{ HO opyie
bb
(iiv) + vdu
b b
(uv)+fudv (uv)—1vdu (uv) — d(uv)
Дата добавления: 2015-10-30; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| HMT YCTPHHMM T0KH 3bIB B TOKX | | | Bbl6epwre epoe YTBP)KLIHH |