TEMA 10. MIICJIOBbIe pnJbI

‘-THCIIOBOH p5I CXO,LFITC5I, ecylH

peeii ero o6mero iea pae HJi[O

HOCI1OBTJThHOCTE ero qaCTW-IHMX CMM orpaeaHOCI1OBTJThHOCTb ero CTI1HMX CMM HMT KOHHbW npeei

IJTHbI pia MOHOTOHHO y6MBaIOT no a6cornoTnoui Be.rwqHHe

‘-IFICIIOBOFI p5I C HOJ1O)KFITJThHMMFI iienan CXOHTC5I, eC.TIH CXOIWTC5I p5rn, JIeHM KOTOOFO MHMIT J1HOB HHOFO piaCXOIWTC5I p5rn, ‘IJICHM KOTOOFO 6oimme JTHOB HHOFO pa

npeeii ero o6wero iea pae HIIIO

3TOT p51 5JBJ15JTC5J rapMOHwICCKFIM

CorilacHo HHTFJThHOM HH3HK CXOHMOCTH, qHC.TIOBOH p5JL C HOJTO)KHTJThHbIMH

fflHMH a,? pacxoHTc51, CCJTFI Heco6cTBeHHJiln nnTerpaji f f(x)dx, r,e f(n)= a

n=1 1

6omme 1

pae 1

pae KOHe’-IHOMy HCJIy 51BJ151TC51 6ecKoHeHo 6oJmmHM

Coriiacno HH3HK CBHCHH5I qHCJIOBOH p5IL C HO.TIO)KHTCJThHMMH LJ1CHMH paCXOHTC5I,

eciin

PaCXO2WTC5J rapMOHw-ICCKHH p5IL

PaCXO2WTC5J p5I, ‘1JICHM KOTOOFO 6oimme q.JTeFIOB LaHHOro papacxownci p5I, ‘1JICHM KOTOOFO MCHbIIIC J1HOB LaHHOrO p5ILa

pacxownci p5i, COCTaBJICHHMH H3 1IJIeHOB reoMeTpH1ecIcoH riporpeccun

Ho HM3HK 4aIIaM6epa, ecrni lim = > 1, TO 5l C IIOJIO)KHTCJThHMMH IJIeHaMH CXOHTC5{

pacxOwTc5J

CXOHTC51 CIIOBHO

MO)KT KK CXO,LHTbC5I, TK H CXOHThC5I

EcYIH qHCJIoBoH p CXOHTC5I, TO peeii o6er’o iena pa pae

—1

—0

4HCOBO p 1+ — + — +... + — +... H3MBTC

23 n

HTJThHMM

FMOHF1CKF1M

— CXO5JWI1MC5I PUHOHJThHbIM

B HCI1OBOM pe

cO2n fl=13n — 1

peeii o6wero iiea pae

—cc

O6IIWM 1I1eHOMp5I,La 6yer

2n +1

2n

1

2n —1

2n

2n—1

cxDl

FapMOHWIeCKIW p51 — 5{BJ15{TC5{

n=lfl

CXOWITJWMC5I PCXOW{TJWMC5I CJIOBHO CXO5JWHMC5I

a6cornoTHo CXO,L5JWHMC5I

c.02n

B ‘-IFICJIOBOM pe peeii o6wero iiea pae

n=132 —1

Ecim MCJTOBOi pi CXOHTC5{, a C — HOCTO5HOC qHCIIO, TO Ca

pacxOwTc5{

CXOHTC51 111111 paCxO2TC5ICXOHTC51 TOJThKO CI1OBHOCXOHTC51

Ecilil P51Wil H

b,7 CXO5JTC5J, TO

n=1

+b) CxOMTc51, a (a,7 — b) pacxowrci

17=1

— P5U (a ± b) CXO2WTC5I

n=1

p (a ± b) pacxO.!rnTc51

(a ± b) CXOMTC51 CIIOBHO

Heo6xoMMbIM IIH3HKOM CXOLHMOCTFI FICJ1OBMX p5ILOB 5JBJ15JTC5J

lima,1 = 0

fl->cjD

lirna,7 = cc

fl—*cC

1ima

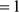
fl—*QC

1ima

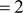
n—*cfj

‘-IFICIIOBOFI p51 pacxo,LU4Tc5I, ec.TIH

Hpe,re.ri ero o6wero ‘uleHa pae HJTIO

HOCIIOBTJThHOCTb ero acmix CMM HMeeT KOHeqHbIH npeeinpeei HOCIIOBTJThHOCTH ero T-IaCTHT-IHbIX CMM 6ecKoHeeH

‘-IFICIIO ‘-LTIeHOB 6ecKoHeHo

CyMMa IICHOB 6ecKoHeqHoii y6bIBaioweii reoMeTpHecKoH porpecc onpeeiiieci nocopMyJIe

b1q

1—q

+

b1 +q(n—1)

BbIpaeHHe a1 + a-, + a3 + + a + H3bIBCTC5IHocI[eoBaTeJmHocmIo

‘-IFICI[OBMM 5{OM

— apH4JMeTw-IecKoFI nporpeccne reoMeTpwlecKoFl nporpeccne

CyMMOii p5{La S H3MBTC5{

cyMMa nepix fl UICHOB

KOHeHbIii npeeii HocIIeLoBaTeJmHocTH CTHHMX CMMnpeeii o6wero nea pa

— OCTTOK p5J,La

Ecirn B qHC.TIOBOM pe npe.LeJ1 o6mer’o iea pae Hy.wEo, TO p5J,L o6w3aTeJmHo CXO)11TC5I

— o6w3aTeJmHo CXOL11TC5J

MO)KT CXOMTbC51, a MO)KT paCxoHmC5I CXOMTC5J a6COIEIOTHO

Ecirn B qI1C.TIOBOM pe npe,LeJ1 o6mero q.rleHa He HyJTIO, TO 5ICXOMTC51

CXOMTC5J

MO)KT CXOMTbC51, a MO)KT CXO11TbC5JCXOMTC51 CJ1OBHO

ECJTh HeCO6CTBeHHMi HHTFJ1 ff(x)dx pae KOHHOM IICI[y, TO COFJ1CHOF1HTFJThHOM HH3HK CXOL11MOCT11 qHC.TEOBOiI p5IL C HOJ1O)KHTJThHMMH q.lleHaMH

a,, = f(n) CXOMTC51 CI1OBHOPCXOWTC5J

CXOWTC51

MO)KT CXOHTbC51, a MO)KT CXO11TbC5J

COFIIaCHO HH3HK CBHH1151 qHCJIOBOH p5JL C HOJTO)KHTJThHMMH qJIeHaMH CXOHTC5I, CJ1H

CXOWTC5{ p5J), COCTaBJIeHHbIH 113 J1HOB reOMeTpHeCKOH HOFCCHHCXOHTC51 p5J, -1I1HM KOTOOFO MHMJI T-LneHOB LaHHOrO p5JLa

‘-LTIeHM LaHHOrO p5I,La MHMII JIHOB LpyrOr’O p5I,Ta

CXOWTC5{ p5J, -1J1eHM KOTOOFO 6ollbme JTHOB HHOFO p5I,Ta

4TO6bI 3HaKOepeLyIOuw11C5I qHCJIOBOH p5IL CXOHY1C5I a6COJTIOTHO, OH,TOJT)KeH

CXOHTbC5{ CI1OBHOCXOHTbC5{ CXOHTbC5{

CXOHTbC5{ CI1OBHO

4IIL5 HCCI1eLOBaHH5I CXOL11MOCTH 3HaKOepeLyIOwHXC5I p5I,TOB HHMH5ITC5I

HHTerpaJmHbIH HH3HK KomilHH3HK CBHHH5J

HH3HK 4IaI1aM6epa

HH3HK JIeH6HHua

HpFI3HaK aJIaM6epa 5{BJ15{TC5{ LOCTaTOqHMM HH3HKOM CXO,THMOCTH 3HaKOepeyfOIuHXC5I P5LTOB

CTHHHMX 5{OB

5{OB C HOJ1O)KHTJThHBIMH q.rleHaMH

— FMOHWICKOFO p5I,La

HHTeFpaJThHMI1 IIF13HK Komn H11MH5ITC5J JT5J HCCJTOBHH5J CXOLIJIMOCTH

p5I,LOB

— qHC.TIOBMX 5IOB C noHo)KHTeJmHbIMH, MOHOTOHHO y6MBa}OmHMH qyleHaMHCTHHHMX 5IOB

CXO5JTIHXC5I 5IOB

Ecm lima,1 0, TO 5J afl

fl-*D n=1

CXOLHTC51 CXOHTC51 CJIOBHO

pacxOrnTc5’

— CXOHTC51 a6COJIIOTHO

3HaKoepeyIouwiicM a CXO,LHTC5I ycHoBHo, ec.r1HOH PaCXO.IWTC5{

p5J pacxO,LHTc5I, a p5J, COCTaB.TIeHHMH H3 a6COJTIOTHMX BCJ1HHH ‘-LnCHOB,LaHHOFO p51a,

CXOHTC51

p51 CXO,LHTC5J, 11 CXOL11TC5I p5J, COCTaBJTeHHMH H3 a6COJTIOTHbIX BeI[HT-IHH ‘-LnCHOB LaHHOrO

pa

5{ CXO,LHTC5J, a p51, COCTaBYIeHHMH H3 a6COJTIOTHMX BeI[HT-IHH ‘-LnCHOB HHOFO p5LLa, CXOHTC5J

3HaKoepeyIouwiic5I ‘-IHC.TIOBOH p5{T CXOLHTC5I a6COJIIOTHO, ec.TIH

CXOHTC5{ p5{,L, COCTaBHCHHbIH 113 a6COII}OTHMX BCIIHqHH HHOB LaHHOrO pia

peeii ero o6ero luleHa Ho a6cornoTHoi BCJTHHHC pae Hy.JTI0 ulCHbI pa Ho a6coJlIoTHoii BeJIHT-IHHe MOHOTOHHO y6MBa}OT BMHOHH5ITC5{ HH3HK JIeH6HHUa

HpH3HaK JIeH6HHUa 5IBJ15ITC5I

Heo6xoHMMM HH3HKOM CXOL11MOCTH 3HaKOepeLy}OwHXC5I p5I,TOB OCTTOHbIM HH3HKOM a6COIIIOTHOH CXOLHMOCT11 3HaKOepeLy}OwHXC5I p5ILOBOCTTOHbIM HH3HKOM paCXOLHMOCT11 p51LOB

OCTTOHbIM HH3HKOM CXOIWMOCTH 3HaKOepeLyIOwHXC5{ p5{,TOB

Ho HH3HK 4aI1aM6epa, CY1H lirn

= £ <1, TO p5IL C HOJ1O)KHTJThHMMH 1I1eHaMu

‘

CXOHTC5J

MO)KT KK CXOHTbC5{, TK H CXOHTbC5ICXOHTC5{

CXOHTC5{ CI1OBHO

B HCJ1OBOM p5{,re pee o6ero iiea pae

=i3n—2

—0

—cc

CyMMa F1CI1OBOFO p5l,La CYmeCTBYeT, eciTH p5I CXOMTC51

CXOMTC5J

— coepKMT 6ecKoHeHoe ‘-IFICJIO T-LneHOBCOKMT TOJThKO Ho.TloKFlTeJmHMe q.TleHJil

Ecirn ‘-IFICJIOBOFI p51,L CXOHTC5J, TO ero fl-Fl OCTTOK

CTMF1TC51 K 6ecKoHeHocm pae HJI[O

CTMF1TC51 K HJT[O

CTMF1TC51 K e.LHHFlue

CorliacHo HH3HK cpaBHeHH5l, HCI[OBO1 p5J a CXOHTC5I, eciTila <—

n

a > —

n

—a<---­

1

—a>­

- H - H - M HX yCIIOBHH HH3HK JIeH6HHUa CXOLHMOCTH p5ILOB 5IBJT5ITC5I

a1 <a a1 > a a1 = a a1 a

4HCJ1OBOii p5{L

, 2n +1

CXOHTC5I HO Heo6xowIMoMy HH3HK CXOIWMOCTH CXOHTC5I HO HHTFJThHOM HH3HK

CXOHTC5I CI1OBHO CXOLHTC5{

414C110B014 p5I.L

— CXOMTC51

=i 3n

— CI1OBHO CXOLHTC5J

— CXOHTC5I a6COIIIOTHO CXOMTC5I

4FICIIOBOH p51.L

2n—i

=i2n +1

— CXOMTC5I CI1OBHO

— CXOMTC51 a6COJIIOTHO

CXOWTC5I 110 Heo6xO,L11MoMy 11H3HK CXOHMOCTH CXOMTC5I

4FICIIOBOFI p51.L

pacxowTc5’

iD1

,i=1

CXOLHTC51 110 11H3HK aJ1aM6epa CXOW1TC51 110 Heo6xo,1u1MoMy 11113HKCXOMTC51 110 11F13HK CBHH115I

4HCJIOBOH P5LT

pacxowTc5{

/ ‘,i+1

t—i

,i=1 3n — 2

CXOWTC51 110 11H3HK aJ1aM6epa CXOHTC51 110 11H3HK JIeH6HHUa

a6cornoTHo CXOHTC5J

/ ‘ii+1 .n

4HCJIOBOFI P5LT

pacxo2wTc5I

ii=1 2n—1

CXOWTC5{ 110 11H3HK 4IaJ1aM6epa CXOHTC51 110 11H3HK JIeH6HHUa

a6cornoTHo CXOHTC5{

(_i)’ .n

n=1 5

1?

pacxowTc5I CXOHTC5{ CI1OBHO

CXOHTC5{ a6COJIIOTHO

MO)KT KK CXOLHTbC5I, TK 11 paCxO,THmC5{

P5I

n=i2W +1

CXOMTC5J

CXOIITC5{ 110 11F13HK JTeI16HHUa CXOWITC5{ 110 11F13HK aJ1aM6epa CXOHTC5{ 110 F1HTFJThHOM 11F13HK

/ ‘,i+1

‘-IFICIIOBOFI 2

11=1 fl +1

— CXOMTC5I

— CXOMTC51 a6COIEIOTHO

CXOMTC51 CJ1OBHO

MO)KT KK CXO,LHTbC5J, TK H paCxOHmC5J

CyMMa FICJ1OBOFO p5I,La

n=1n +3

paa KOHe’-IHOMy qHCI[y He CYLUCTBYT

6ecKoHeHa

paa HJTIO

CyMMa ‘-IHCJIOBOFO p5ILa

iD1

11=1 fl + 1

paa KOHe’-IHOMy HCJI

6ecKoHeHa

paa HJTIO

paa 1

CyMMa ‘-IHCJIOBOFO p5ILa

He CYLUCTBYT

6ecKoHeHa

-/ 1 ‘,i+1

)

11=1 fl

paa KOHe’-IHOMy HCI[

paa 2

O6WHM J1HOM pia 1— + — — — + 6y,er

1

2n +1

(_ 1)/il

2n —1

(_ 1)/il 2n+1

1

2n —1

TEMA 11. KOMIIJIeKCHbIe ‘iiicjia

4FICIIO l H3MBTC5I MHMMOk e,LnHMueM, ecrni

.2

—1=—

—I =—1

i=—1

.4

—1=—

K KOMHI1KCHOM T-IMCI[y X + ij) COH5DKHHMM 5IBJ15ITC5I KOMHJ1KCHO 1IHCJIO

y+ix x—iy y—ix ix—y

CyMMa KOMHJ1KCHMX qllce.TI Z1 = + l3) Fl Z2 = X2 + lj) oHpe,LeJI5IeTc5I HO 4)opMylle

Z1 +Z2 = (x1 +y2)+i(x7 +yi) Z1 + Z2 = (x1 + x2) — i(y1 + Y2) Z1 + Z2 = (x +x2)+ i(y1 + Y2)

z1 +z2 =x1x2 +iy1y2

EcilM Z =2+3i,To Z2 BHO

12i—5

— 13+12i

—-5

—13

Pa3Hocm ,LWyX KOMHJ1KCHMX qHce.T1 Z1 = X1 +13) H Z2 = + iy2 ollpeLeJ15IeTc51 no

dopMy.rle

Z1 — Z2 = (x1 — x2) — i(y1 — y2)

z1 — z2 = — iy1y2

Z1 — Z2 = (x — Y2) + i(x2 — y1)

Z1 — Z2 = (x1 — x2) + i(y1 3)2)

HpoH3BeeHHe BX KOMHJ1KCHMX cei Z1 = + i))1 H Z2 = X2 + i))2 BHO

Z1Z2 = (x1x2 — y1y2) + i(x1y2 + x2y1) Z1Z2 =(x1x7 +y1y7)+i(x1y7 —x7y1) z1z2 =x1x2 —iy1y2

z1z2 = x1x2 + iy1y2

EcJIH Z=x+ly,To Z BHO

x2 +2ixy+y2(x2 —y2)+2ixy

—x 2 +y 2

(x2 +y2)—2ixy

Ecm Z = X + 1)) M Z = X — iy, TO ZZ BHO

x2 —y2

(x2y2)

—(x +y) y2 —x2

Ec.nM Z =x—iy,TO Z2 BHO

x2 —y2

(x2 +y2)—2ixy

(x2 —y2)—ixy

(x2 —y2)—2ixy

BbIpaeHHe (3 + 2i)(3 — 21) BHO

—9—41

—9+4j

Ecim Z = x + 1)) II Z = x — iy, TO Z — Z BHO

2x

2(x-iy)

Iy

Ecrn Z = x + iy H Z = x — iy, TO BHO

—1+

2ixy

x2 +y2

—1— 2ixy

x2 —y2

2ixy

x2+y2 x2+y2

Ec.r1H Z =x+iy,To iZ BHO

y+ix x2+y2

(—y + ix)

ix

Ec.r1H Z1 = x + 2iy, Z2 = 2x —1)), TO Z1Z2 BHO

2(x2 —y 2 )+3ixy

2(x2

-y 2 )

—2(x 2 +y 2 )+3ixy

2(x2

+y 2)

Ecm Z = x + ly, TO Z3 BHO

x3+iy3

— y3

(x3 +3xy2)—i(3x2y+y3) (x3 —3xy2)+i(3x2y—y3)

Ecw Z = x — ly, TO Z3 BHO

“ j—i3 “

(x —3xy.1 ry—y

x3 — y3

x3+y3

(x3 —3xy2)+i(3x2y—y3)

Ec.rrn i — MHHM5{ e,nHHHua, TO BHO

—1

K KOMHJIKCHOM ‘-IHC.Lly X — iy COH5DKHHMM 5IBJ15{TC5I KOMHJIKCHO HCJIO

y—ix y+ix x+iy

-x-iy

EcnH i — MHHM5{ eHHHua, TO BHO

—1

Ec.r1H Z1 = x + 2iy, Z2 = 2x +1)), TO Z1 + iZ2 BHO

3(x+iy) (x+y)+2i(x+y)

(x — y) + 2i(x + y)

(x—y)—2i(x+y)

EcilM Z = x + iy Fl Z = x — ly, TO Z + iZ BHO

(x + y) + i(x — y)

(x — y) + i(x + y)

(x + y) + i(x + y)

(x + y) — i(x + y)

Ec.rlM Z = x + iy Fl Z = x — iy, TO Z — iZ BHO

(x + y) — i(x — y)

(x - y) - i(x - y)

(x — y) — i(x + y)

(x — y) + i(x — y)

EcliM I — MHMM5{ e,LHHHua, TO BHO

—1

Ec.rrn Z =x—iy,To iZ BHO

—y+ix y+ix x+y

ix

CyMMa KOpHeiI KBaLqDaTHOFO BHHH51 x2 + 2x +17 = 0 paa

—2

Ecim x1 H — KOHH KBTHOFO BHHH5I x2 — 6x +25 = 0, TO X2 BHO

25

—7

—1

Ecm x1 ii — KOHM BHHII51 + 4x +13 = 0, TO BHO

x2

—2

—3

5 12.

13 13’

12.

1+—i

5

Ec.nM X1 II — KOH11 BHHF151 — 8x +25 = 0, TO (x1 — x2 )2 BHO

—0

—36

—9

—36

EcilM X1 II — KOH11 BHHF151 + 5x +25 = 0, TO X2 BHO

12,5

——12,5

—25

—25

Ec.nM X1 II — KOH11 BHHF151 — 6x +13 = 0, TO (x1 — x2 )2 BHO

—16

—0

——16

—36

Ec.nM X1 II — KOHF1 BHHH5I x2 +9 = 0, TO X, BHO

—9

——9

—6

——6

Ec.nH X1 H X2 — KOHH BHHH5I — 7x + 18,5 = 0, TO X1 + X2 BHO

—7

—14

—5

—0

EcrnZ1=5+4iHZ2=3+i,To paBHO

+41

1,1 + 0,71

1,9 + 0,7i

19 7.

8 8

z

EciZ1=3+ 2IM Z2 =6— 41, TO paBHO

EcJmZi=6_51MZ2=4+31,T0Z1_Z2 BHO

—24—24i

—36—841

—4—841

16—241

EcIIMZ=3 +41, TO Z3paBHo

171 — 1721

——117—44i

—27—64i

—27+64i

Ec.rill Z= 3 — 21, TO BHO

—27—81

—63 +461

—27+81

—9 + 461

Ecrn Z1 = 1 —21 ii Z2 = 2 + 31 ,TO Z Z2paBHo

—6—171

——6—91

10 + 151

—6+171

EC.TIFI Z1 = 4 + 3i M Z2 = 2 — 3i, TO 1* Z2 BHO

——28—211

—88—91

—48+331

16—631

2 2

EC.TIM X1 Fl X2 —IcopIwypaBFleFrnsl x —lOx+34=O ,TO X1 X2 BHO

—601

—901

—0

——36

2 2

EC.TIM X1 LI X2 — KOHFI BHHH5J x — 12x +40= 0, TO X1 + X2 BHO

—72

—64

—481

—12

Дата добавления: 2015-10-30