Переходная характеристика.

Типовые динамические блоки

Независимо от различного физического характера, компоненты систем управления могут иметь подобные дифференциальные уравнения и могут быть собраны в следующие шесть групп:

Пропорциональное звено;

Звено первого порядка;

Звено второго порядка;

Интегратор;

Дифференциатор;

Звено запаздывания.

Когда отдельный элемент системы слишком сложен, чтобы рассматриваться как один из вышеупомянутых блоков, то он может быть представлен комбинацией нескольких типовых блоков. Использование типовых блоков обеспечивает инженера проектировщика удобным способом описать и смоделировать систему управления, которая может состоять из многих компонентов и иметь сложную конфигурацию.

Рассмотрим 6 групп систем управления с точки зрения следующих определений:

Дифференциальное уравнение;

Физика процесса

Передаточная функция;

Характеристическое уравнение. Полюса.

Переходная функция;

Примеры.

ИСХОДНЫЕ ДАННЫЕ ДЛЯ ЛЕКЦИИ №4

Пусть система управления описывается блок-схемой:

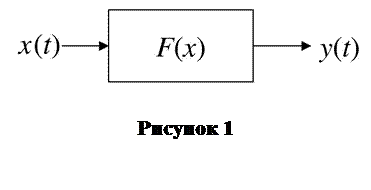
где x (t) - входной сигнал,

y (t) - выходной сигнал.

ПРОПОРЦИОНАЛЬНОЕ ЗВЕНО

1. Уравнение.

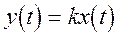
k - параметр звена (усиление).

2. Физика процесса. Вышеуказаное уравнение, которое не является дифференциальным уравнением, указывает, что звено представляет статическую систему, то есть систему с незначительной инерцией. Например, инерция электронного усилителя движения электрического двигателя незначительна по сравнению с инерцией двигателя; поэтому, усилитель может рассматриваться как постоянный элемент усиления. Необходимо понять, что тот же самый усилитель, используемый в пределах электронного электропитания, не был бы описан как пропорциональное звено, потому что его инерция сопоставима с инерцией остальной части компонентов.

3. Передаточная функция. В соответствии со свойствами преобразования по Лапласу, :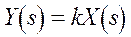

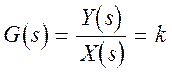
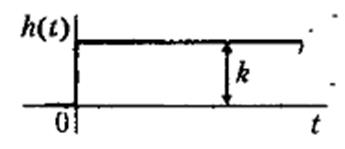
Переходная характеристика.

Примеры

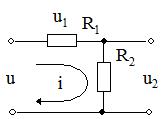
Рисунок 1 - Четырехполюсник с сопротивлениями

Рисунок 2 - Редукторная передача

Уравнение.

АПЕРИОДИЧЕСКОЕ ЗВЕНО ПЕРВОГО ПОРЯДКА

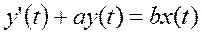
где " a " - положительный параметр, представляющий собой инерцию системы.

2. Физика процесса. Вышеупомянутое уравнение типично для многих физических явлений, где инерция проявляется, в противопоставление внешнему воздействию. Однако, системы первого порядка способны к хранению только одной кинетической энергии (или ее немеханические эквиваленты). Например, уравнение движения механической системы, не содержащей любые элементы жесткости, может быть описано как:

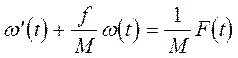
где M, f, ω(t), F (t)соответственно масса, коэффициент вязкости, коэффициент трения, скорость, и функция внешнего воздействия (Вал).

Подобное уравнение электрической цепи:

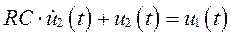
может быть написано для RС –электрического контура (где C, R, u (t) – емкость, сопротивление, напряжение).

3. Передаточная функция. Преобразование по Лапласу 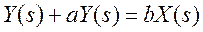приводит к:

b

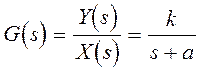(1)

Стандартная форма передаточной функции:

где k – коэффициент усиления или передачи системы,

T – постоянная времени (sec)

Дата добавления: 2015-10-30