Уравнения Колмогорова

Для достаточно малого конечного промежутка времени Δt вероятность перехода системы из некоторого i-ro состояния в состояние номера j пропорциональна, в первом приближении, длине этого промежутка:

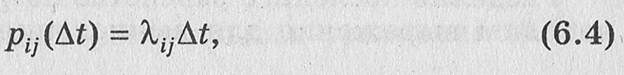
где λ_ij - плотность вероятности перехода.

Пусть в некоторый произвольный момент времени t систе­ма находится в любом i-м из R возможных состояний. Через достаточно малый промежуток времени Δt система окажется в конкретном состоянии номера s, вероятность чего примерно равна

с выделением s-гo слагаемого и соседних с ним, а также с учетом соотношения (6.4) ее можно записать в следующем виде:

Преобразуем последнее соотношение путем замены s-ro слагаемого в правой части эквивалентным ему выражением, не содержащим λ_ss. Для этого примем во внимание, что если в некоторый начальный момент времени t система находилась в исходном состоянии номера s, то в течение Δt она может перейти в любое из возможных состояний, включая также ис­ходное, что можно выразить уравнением

Из последнего уравнения определим вероятность того, что система останется в исходном состоянии:

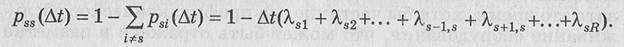
Подставляя найденное выражение для p_ss(Δt) в формулу (6.5) и вычитая из правой и левой частей p_s(t), найдем прира­щение вероятности s-ro состояния системы за промежуток времени Δt:

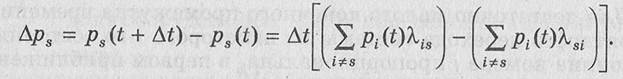
Разделив последнее равенство на Δt и переходя к пределу, находим выражение для вычисления производной

Полученная система дифференциальных уравнений носит имя Колмогорова. Решение задачи Коши для указанной сис­темы позволяет определить функции вероятностей состояний марковской системы в произвольный момент времени.

Если на СМО воздействуют простейшие потоки случайных событий, что ограничивает множество возможных переходов, уравнения Колмогорова приобретают более простой вид

Математическая модель СМО в виде системы дифференци­альных уравнений (6.7) соответствует графической модели, представленной на рис. 6.1, и будет использована нами в даль­нейшем для анализа стационарного режима работы системы.

6.6. Финальные вероятности состояний СМО

Решение задачи Коши для системы уравнений (6.6) при заданных начальных условиях приводит к получению систе­мы функций времени:

Это позволяет получить дискретное распределение вероят­ностей на множестве состояний СМО для любого значения t >= 0. Анализ решения показывает, что для достаточно боль­ших 'значений t, независимо от начальных условий, это распре­деление стабилизируется и практически не зависит от време­ни. Указанное асимптотическое свойство решения означает, что с течением времени функционирование СМО переходит в стационарный режим, соответствующий постоянству значений функций (6.8):

Система значений вероятностей состояний, соответствую­щих стационарному режиму работы СМО, называется финаль­ными вероятностями.

Полагая в системе дифференциальных уравнений (6.6).

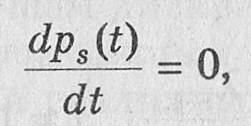
получаем для определения финальных вероятностей следую­щую систему алгебраических уравнений:

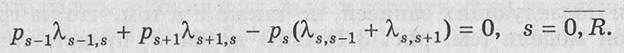
Для наглядности запишем несколько первых уравнений данной системы для различных значений s:

Используя первое из этих уравнений, соответствующее s=0, выразим р₁ через р₀:

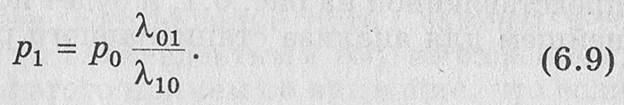
Производя преобразования второго уравнения, соответству­ющего s=l, найдем аналогичное выражение для р₂:

используя (6.9) запишем

и окончательно находим

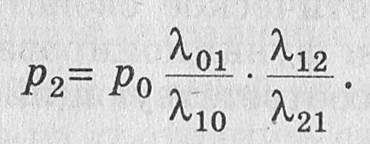
Продолжая этот процесс найдем для любого состояния СМО номера s, выражение р_s через р₀:

Введем обозначение

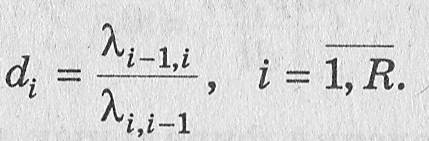
Удобство введенного обозначения состоит не только в крат­кости последующих записей, но также и в том, что на графи­ческой модели (см. рис. 3.1) СМО дроби di. представлены в явном виде. Плотности вероятностей переходов слева от i-ro состояния рядом с прямой и обратной стрелками являются соответственно числителем и знаменателем дроби такого же номера. Это особенно удобно при анализе небольших СМО. В этом случае при разметке графа состояний СМО целесообраз­но записывать плотности вероятностей переходов не в общем виде, а их числовые значения, что будет проиллюстрировано ниже при рассмотрении конкретного примера/

С учетом введенных обозначений соотношение (6.10) мож­но записать короче:

Поскольку сумма вероятностей всех состояний равна единице

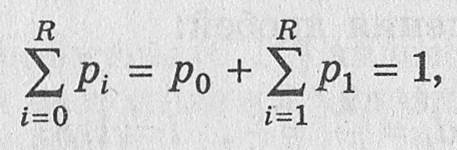
то с учетом формулы (6.11) запишем уравнение для определе­ния р₀:

откуда получим формулу для вычисления вероятности сво­бодного состояния:

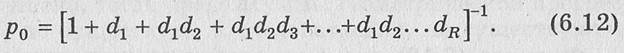
По формуле (6.11) вычисляются остальные вероятности. Справедлива рекуррентная формула

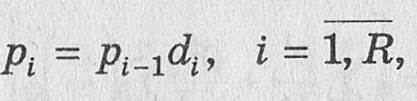
применение которой особенно удобно при анализе СМО с не­большим числом состояний.

Таким образом, получаем дискретное распределение веро­ятностей на множестве возможных состояний СМО. Это дает возможность определения различных характеристик системы как средних значений соответствующих случайных величин, что будет сделано в следующих параграфах.

Полученные формулы (6.11), (6.12) для вычисления диск­ретного распределения финальных вероятностей на множестве состояний системы удобны в том случае, когда число мест в очереди т невелико. Часто указанные формулы полезны при анализе замкнутых систем.

Когда число mболее 10, вычисления по формуле (6.12) ста­новятся утомительными. Особенно затруднено будет примене­ние указанной формулы в случае неограниченности очереди, поскольку при вычислении суммы в квадратной скобке в фор­муле (6.12) придется ограничиться конечным числом слагае­мых. Чтобы избежать трудностей, целесообразно получить формулы более приспособленные для случаев, когда возника­ют названные проблемы. Ниже это будет сделано только для разомкнутых систем. Что касается замкнутых систем, то это могло бы быть сделано аналогично и особых трудностей не представляет.

Рассмотрим n-канальную систему с допустимой длиной очереди m, графическая модель которой представлена на рис. 6.1. С учетом разметки графа можно записать следующие формулы для вычисления дробей:

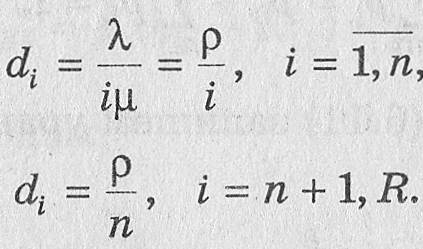
Здесь использовано общепринятое обозначение относитель­ной нагрузки на систему

Формула (6.12) для вычисления вероятности свободного состояния с учетом введенных обозначений приобретает сле­дующий вид:

Замечая, что в последнем соотношении присутствует сум­ма геометрической прогрессии

получаем формулу, более удобную для вычислений:

Если же длина очереди не ограничена, переход к пределу при гаг стремящемся к бесконечности позволяет получить для вычисления вероятности свободного состояния системы не­сколько более простую формулу:

Использование формулы (6.15) является корректным лишь в том случае, когда выполняется условие существования ста­ционарного режима СМО

Смысл этого условия состоит в том, что суммарная интен­сивность обслуживания, создаваемая всеми га одновременно работающими каналами, равная nμ, должна быть строго боль­ше интенсивности входного потока заявок λ Если же это ус­ловие нарушено, тогда предел суммы геометрической прогрес­сии (6.13) не существует, а следовательно, не существуют и финальные вероятности.

Используя соотношение (6.11) запишем формулы для вы­числения остальных вероятностей:

Иногда вместо формулы (6.19) более удобно пользоваться рекуррентной формулой

Использование соотношений (6.14)-(6.20) позволяет опре­делить основные характеристики системы, имеющие важное значение в экономическом анализе СМО. Это будет сделано ниже.

Дата добавления: 2015-10-23