Очередь в процессах обслуживания

Часть заявок, принятых в СМО и ожидающих обслуживания, называется очередью. С точки зрения тех, кого обслуживают, очередь связана с бесполезной потерей времени и всегда ассоциируется только с отрицательным восприятием. Одной из важнейших экономических характеристик СМО является время, теряемое заявкой в очереди на ожидание обслуживания. Большое количество заявок, ожидающих обслуживания, кроме отрицательного влияния на субъективное восприятие, мешает нормальной работе даже при небольших временных затратах. Хорошо организованное обслуживание соответствует реально незначительному времени нахождения заявки в очереди. В условиях рыночной экономики и при наличии конку -ренции низкий уровень обслуживания приводит к потере потенциальных заявок и снижению конкурентоспособности. Поэтому для менеджера важным является контролировать процессы образования очереди. Пренебрежение этой стороной менеджмента может привести к серьезным экономическим потерям, вплоть до вытеснения из рынка. Теория массового обслуживания дает методы анализа характеристик очереди и выявления путей ее уменьшения.

Формирование очереди, а следовательно и ее характеристики, зависит как от поведения заявок, так и установленных со стороны СМО правил отбора заявок из очереди на обслуживание. Правила формирования очереди называют дисциплиной очереди.

0о стороны заявок дисциплина очереди зависит от ограничений, связанных:

• с длиной очереди, или, числом мест в очереди;

• предельным временем пребывания заявки в очереди.

Со стороны СМО дисциплина очереди определяется:

• правилом отбора заявок на обслуживание;

• установлением приоритета в обслуживании отдельных категорий заявок.

Экономическая эффективность СМО зависит от указанных механизмов формирования очереди.

6.4. Графическая модель СМО

6.4.1. Разомкнутая простейшая СМО

Рассмотрим систему массового обслуживания, состояние которой не влияет на поток заявок, требующих обслуживания, т. е., характеристики входного потока заявок не зависят от того, сколько заявок уже находится в системе в данный момент.

Приступая к построению модели, уточним, что она нам нужна для исследования динамики изменчивости состояний моделируемого объекта. Исходя из определения понятия модели как отражения моделируемого объекта, а также с точки зрения дальнейшего использования графической модели системы массового обслуживания, отобразим в модели существенные для последующего анализа моделируемого объекта элементы трех типов:

1) множество возможных состояний моделируемого объекта;

2) возможные переходы состояний;

3) закономерности, в частности интенсивности переходов. Условимся различать состояния СМО по числу находящихся

Рис. 6.1. Графическая модель СМО разомкнутого

в ней заявок. Пусть п - число каналов СМО, am- число мест в очереди, конечное или бесконечное. Тогда в системе может находиться от 0 до R = п + т заявок. На рис. 6.1 состояния системы изображены в виде различных, для наглядности, геометрических фигур с указанием количества заявок, которому соответствует это состояние. Так, прямоугольниками представлены состояния, соответствующие отсутствию очереди, при которых число заявок не превышает числа каналов. Свободное же состояние, когда в системе нет ни одной заявки, выделено в виде окружности, внутри которой помещено число 0. Состояния, соответствующие наличию очереди, изображены в виде овалов, кроме наиболее загруженного состояния, которое представлено в виде прямоугольника с числом п + т внутри него.

Возможные изменения состояний системы изображены на рис. 6.1 в виде стрелок, соединяющих различные состояния с указанием направлений переходов. Любой из переходов связан с изменением числа заявок, находящихся в системе, ровно на единицу, в большую или меньшую сторону. Каждый из переходов соответствует событию одного из двух типов. Это может быть событие, состоящее с приходом в систему очередной заявки на обслуживание, в результате чего число заявок увеличивается на 1. Событие противоположного типа приводит к уменьшению числа заявок на 1 и является следствием обслуживания в СМО любой из находящихся в ней заявок любым из каналов. Таким образом, представленные на рис. 6.1 переходы предполагают, что в системе никогда не происходят одновременно хотя бы два из возможных событий. Иначе говоря, если СМО находится в состоянии номера i, то оно может смениться только одним из двух состояний, номеров i - 1 или i + 1. Причиной указанного ограничения возможных переходов является предположение о том, что на систему воздействуют простейшие потоки случайных событий, обладающие, как известно, свойством ординарности. В крайних состояниях системы, номеров 0 и n + m, возможно событие только одного из названных типов.

Полученная структура модели является ориентированным графом, если его вершинами считать события, а дугами - переходы. Как легко заметить, этот граф вытянут в цепочку, иногда называемую цепочкой гибели-размножения. Это довольно образное название графа состояний связано с его применением в биологии для исследования динамики колебания численности популяций животных, что возможно в рамках теории массового обслуживания. Для математического анализа является вполне обычным, что одна и та же модель применяется для описания совершенно различных, на первый взгляд, объектов.

Множество стрелок на рассматриваемой графической модели изоморфно множеству возможных событий, которые происходят в моделируемом объекте. Для окончательного построения модели требуется указать числовые характеристики переходов, определяющих склонность системы к изменению своего текущего состояния. Для этого примем во внимание, что вероятность свершения событий, соответствующих верхним стрелкам, т. е. перехода в более загруженное состояние, обусловлена воздействием на систему входного потока случайных событий и пропорциональна его интенсивности обозначаемую символом λ. Поэтому на рис. 6.1 рядом с каждой стрелкой перехода в более занятое состояние помещена указанная интенсивность перехода λ. Переход системы в более свободное состояние определяется интенсивностью обслуживания и равна iμ, где μ - интенсивность обслуживания одним каналом при непрерывной его работе, a i - число работающих каналов. Если номер состояния не меньше числа каналов п, то интенсивность обслуживания стабилизируется и равна пμ

. Таблица 6.1

Таким образом, нами получена графическая модель системы массового обслуживания в виде размеченного ориентированного графа ее состояний изображенного на рис. 6.1. Вид графической модели зависит как от числа каналов п, так и от допустимой длины очереди т. По указанным признакам различаются ряд типов СМО, перечисленных в табл. 6.1.

Каждый из указанных в табл. 6.1 типов СМО охватывается графической моделью, представленной на рис. 6.1. Рассмотренные выше модели СМО характеризуются тем, что интенсивность входного потока заявок является неизменной и не зависит от состояния системы. Случайные события, происходящие в системе, никак не влияют на популяцию заявок. Системы такого типа принято называть разомкнутыми.

Примером СМО замкнутого типа является система обслуживания оборудования. Обслуживание оборудования может быть как профилактическим, так и аварийным. Существенным различием указанных типов обслуживания является то, что если время профилактического обслуживания заранее известно, моменты возникновения потребности в аварийном обслуживании являются случайными. Можно предположить, что качество обоих видов обслуживания зависит от числа обслуживающих бригад.

Характерной особенностью обслуживания в этом случае является то, что множество потенциальных заявок существенно зависит от числа обслуживаемых заявок, т. е. от состояния системы.

Возможно рассмотрение двух случаев:

1) создаются универсальные обслуживающие бригады, способные осуществлять оба вида обслуживания;

2) создаются специализированные бригады двух типов соответственно двум типам обслуживания.

Очевидно, что при разделении двух типов обслуживания, организация процесса профилактического обслуживания нам не интересна, поскольку чаще мы будем иметь дело с регулярными потоками событий, и поэтому потерь времени обслуживающих бригад можно легко избежать, создав детерминированное расписание обслуживания оборудования в соответствии с его техническими особенностями.

Создание универсальных бригад можно связать с организацией гарантийного ремонта. Но сначала исследуем случайный процесс только аварийного ремонта.

Мы здесь не будем уделять внимания профилактической ремонтной службе, направленной на поддержание надежности оборудования на некотором достаточно высоком уровне, поскольку профилактическое обслуживание производится по определенному техническими условиями регламенту, и поэтому время его производства не является случайным.

Рассмотрим случай, когда независимо работающая профилактическая служба обеспечивает надежность работы оборудования на заданном уровне, зависящем от затрат на осуществление обслуживания и от числа обслуживающих бригад. Логично предположить, что вероятность возникновения аварийного вызова пропорциональна числу работающих единиц оборудования. Будем пока считать, что все исправное оборудование находится в эксплуатации и резерв его не предусмотрен. Тогда не требуется учитывать характер ремонта, зависящий от имеющихся исправных единиц для замены вышедшего из строя оборудования.

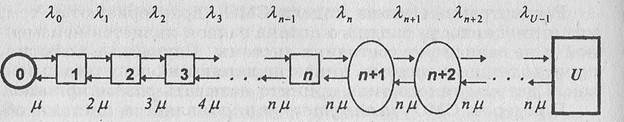
Рис. 6.2. Графическая модель замкнутой СМО

Обозначим через U общее число единиц имеющегося обору­дования, чать из которого, в среднем в количестве и в течение единицы времени, требует аварийного ремонта. Тогда интен­сивность потока заявок, требующих аварийного ремонта, зави­сит от числа уже находящихся в ремонте единиц оборудова­ния, которое обозначим через i, и может быть вычислена по формуле:

где U-i - число единиц оборудования находящегося в эксплу­атации;

u/U -доля оборудования, требующая ремонта в единицу вре­мени.

Графическая модель СМО будет иметь вид, представленный на рис. 6.2.

Очевидно, что если число единиц оборудования, требующе­го ремонта, не превышает числа ремонтных бригад п, очередь в системе не образуется, и обслуживание каждой поступающей заявки начинается немедленно. Особенностью системы данно­го типа является то, что чем больше заявок находится в систе­ме, тем меньше интенсивность входного потока. В состоянии номера U, при котором все, без исключения, единицы оборудо­вания требуют ремонта, интенсивность входного потока, обо­значенная на рис. 6.2 через Х_и_₁, будет равна нулю.

Наличие резерва исправного оборудования требует внесе­ния некоторых изменений в разметку графа состояний. При этом требуется задать размер резерва и среднее время, или среднюю интенсивность как обратную величину времени за­мены аварийной единицы оборудования на исправную. Тогда интенсивность обратного перехода будет сохраняться неизмен­ной и равной интенсивности замены до тех пор, пока число заявок не превышает размера резерва и числа бригад (кана­лов) в системе. Дальнейшая разметка стрелок (событий) обратного перехода зависит как от наличия свободных бригад, так и от наличия резерва исправного оборудования. Нужно также учитывать динамику восстановления резерва. Здесь имеется довольно большое разнообразие типов систем в зави­симости от типа входного потока и от состояния системы. Подчеркнем главное - графическая модель СМО, включаю­щая разметку графа состояний, однозначно определяет вероят­ностные характеристики эффективности работы системы.

До сих пор предполагалась полная идентичность каналов в отношении скорости обслуживания. Если же для каждого ка­нала существует индивидуальная интенсивность обслужива­ния, то при разметке графа состояний следует учесть дисцип­лину вступления в работу свободных каналов.

В случае создания комплексных бригад ощущается более высокая их экономическая эффективность. Это объясняется тем, что уменьшаются потери времени ремонтных бригад на ожидание аварийных заявок, поскольку они могут использо­вать это время, хотя бы частично, на профилактическое обслу­живание оборудования, что может быть отражено в разметке графа состояний.

Общей особенностью замкнутых СМО является конечное число возможных состояний, их анализ.

Дата добавления: 2015-10-23