Тренд-сезонні економічні процеси і їх аналіз

Сезонність, як правило, пов’язується виключно зі зміною природно-кліматичних умов у рамках обмеженого проміжку часу – річного періоду. Найяскравіше цей зв’язок видно там, де досліджувані процеси прямо пов’язані з природними особливостями тієї або іншої пори року: в сільському господарстві, добувних галузях, галузях легкої промисловості та ін. Проте сезонні коливання формуються не лише під впливом природно-кліматичних чинників, але, хоч і меншою мірою, під впливом інших особливостей системи.

Вплив сезонності на економіку цілком очевидний і проявляється в аритмії виробничих і інших процесів: недовантаження виробничих потужностей в одні періоди року і інтенсивніше їх використання в інші; нерівномірний розподіл протягом року обсягів вантажообігу і товарообігу і т.д. Не у всіх випадках сезонність є наслідком дії некерованих або майже некерованих чинників. Найчастіше вони піддаються регулюванню. Але навіть і в тих випадках, коли пряма дія на процеси, що викликають сезонні коливання, неможлива, необхідно враховувати їх дію при вдосконаленні технологічних, організаційно-економічних процесів і процесів управління. Для того, щоб можна було цілеспрямовано впливати на сезонність, необхідно уміти вимірювати і аналізувати сезонність, уміти передбачати розвиток процесів, схильних до сезонних коливань.

Під сезонними коливаннями розуміють регулярні, періодичні внутрішньорічні підйоми і спади виробництва, вантажообігу і товарообігу і т. д., пов’язані зі зміною пори року, а під сезонністю – обмеженість річного періоду робіт під впливом того ж природного чинника.

Якщо процес схильний до періодичних коливань, що мають певний і постійний період, рівний річному проміжку, то ми маємо справу з так званим тренд-сезонним часовим рядом (сезонним часовим рядом).

Розглядатимемо тренд-сезонний часовий ряд , що породжується адитивним випадковим процесом:

, (12.15)

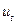де – тренд; – сезонна компонента; – випадкова компонента; 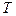– число рівнів спостереження.

Відносно передбачається, що це деяка гладка функція, міра гладкості якої заздалегідь невідома. Сезонна компонента має період : ( = 12 для ряду місячних даних; = 4 – для ряду квартальних даних).

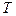Крім того, відомо, що без остачі ділить , тобто 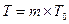, – ціле число. Очевидно, якщо – число місяців або кварталів в році, то – число років, представлених в часовому ряді 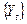. Часто початкові дані тренд-сезонного часового ряду представляються у вигляді матриці розміру . В цьому випадку вираз (4.19) перепишеться з урахуванням введення подвійної індексації:

(12.16)

Запишемо співвідношення, що встановлюють зв’язок між індексами 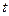і :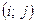

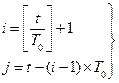(12.17)

означає, як і вище, цілу частину.

Виділимо і коротко охарактеризуємо завдання, що виникають при дослідженні сезонності взагалі і сезонних тимчасових рядів зокрема. Проблема аналізу сезонності полягає в дослідженні власне сезонних коливань і у вивченні того зовнішнього циклічного механізму, який їх викликає. Для дослідження сезонних коливань поза зв’язком з причинами, що їх, що породжують, очевидно, необхідно відфільтрувати з часового ряду 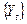сезонну компоненту і потім вже аналізувати її динаміку. Більшість методів фільтрації побудована таким чином, що заздалегідь виділяється тренд, а потім вже сезонна компонента. Тренд в чистому вигляді потрібний і для аналізу динаміки сезонної хвилі.

При дослідженні сезонної хвилі найчастіше передбачається, що вона не змінюється рік від року, тобто , . На практиці таке припущення далеке від дійсності, принаймні для більшості економічних процесів. Для сезонної хвилі характерна зміна з часом як її розмаху, так і форми. В результаті виникає необхідність в аналізі і прогнозі змін сезонної хвилі.

Завдання дослідження сезонних часових рядів:

– визначення наявності в часовому ряду тренду і визначення ступеня його гладкості;

– виявлення наявності в часовому ряду сезонних коливань;

– фільтрація компонент ряду;

– аналіз динаміки сезонної хвилі;

– дослідження чинників, що визначають сезонні коливання;

– прогнозування тренд-сезонних процесів.

Під мірою гладкості тренду розуміють мінімальний степінь полінома, що адекватно згладжує компоненту .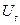

Виявлення наявності в часовому ряду сезонних коливань зводиться до перевірки на випадковість залишкового ряду:

(12.18)

Під фільтрацією компонент ряду розуміють виділення з ряду 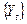його складових , , .

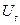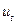Аналіз динаміки, або еволюції, сезонної хвилі може розглядатися як процес розв’язання трьох взаємопов’язаних задач:

– аналіз динаміки амплітуди сезонної хвилі в кожному місяці (кварталі, тижні);

– аналіз динаміки точок екстремуму сезонної хвилі;

– дослідження змін форми хвилі.

На рис 4.1 приведена укрупнена схема дослідження сезонних часових рядів. Схема визначає сукупність і послідовність питань, які мають бути вирішені для повного дослідження сезонного часового ряду. Методи розв’язання кожної задачі можуть змінюватися.

Рис. 12.1. Схема комплексного дослідження тренд-сезонних часових рядів

Управління сезонністю повинно спиратися на знання законів її еволюції, на знання зовнішнього середовища, в якому відбувається розвиток процесу, схильного до сезонних коливань.

Проілюструємо окремі питання аналізу сезонності в економічних процесах на конкретних даних.

В табл. 12.6 приведений часовий ряд щомісячних обсягів перевезень вантажів морським транспортом в умовних одиницях. На рис. 12.2 представлені щомісячні обсяги перевезень за 1-ий, 4- ий, 7-ий, 10-ий і 13-ий роки, тобто з дискретністю три роки. Візуально неважко помітити, що досліджуваному ряду властивий зростаючий тренд і підйоми, що повторюються з року в рік, і спади обсягів перевезень в одні і ті ж періоди року, т. т. сезонні коливання. Таким чином, процес, що характеризується цим часовим рядом, відноситься до тренд-сезонних економічних процесів. Для цього ряду = 12, = 13, так що 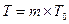= 156.

Таблиця 12.6. Обсяги перевезень вантажів морським транспортом в умовних одиницях

Рік	Місяць
	7,62	6,80	9,02	9,67	10,76	11,48	11,43	11,68	11,20	10,77	9,34	9,55
	8,50	8,11	9,93	10,70	11,24	11,98	12,38	12,73	11,84	12,19	10,97	10,63
	9,40	9,00	11,44	11,73	13,05	13,09	13,74	13,74	12,41	12,69	10,68	10,45
	8,84	10,18	11,64	12,49	13,28	13,63	13,88	13,82	13,11	12,96	12,01	10,75
	9,15	8,02	10,87	12,01	13,96	14,39	14,41	14,45	13,56	13,39	12,40	12,05
	10,8	10,24	12,63	13,50	15,03	15,33	15,24	15,02	14,51	14,12	13,09	12,35
	11,86	11,47	12,81	14,34	15,54	15,61	15,22	15,83	15,46	14,83	13,93	14,00
	10,84	11,55	13,31	14,78	16,08	16,60	16,41	16,72	16,65	15,68	14,67	14,75
	12,19	12,48	14,84	15,65	16,85	17,32	17,69	17,62	16,39	16,37	15,19	14,17
	13,21	12,46	15,33	16,40	17,44	17,26	17,89	17,76	16,97	16,85	15,78	14,86
	14,08	13,19	15,26	16,30	17,78	1&.07	18,31	18,71	18,25	17,70	15,87	16,47
	14,73	13,66	17,59	17,74	19,97	19,28	19,44	19,95	19,58	18,23	17,41	16,87
	14,29	14,32	17,50	18,10	19,82	19,71	19,94	20,94	19,96	19,31	18,52	17,85

Рис 12.2. Обсяги перевезень вантажів морським транспортом в умовних одиницях

Застосування методу Фостера-Стьюарта для часового ряду, представленого в табл. 12.6, дає наступні значення статистик Стьюдента для ряду в середньому і дисперсії:

При рівні значимості , т.т. з довірчою вірогідністю 0,95, і при числі ступенів свободи табличне значення критерію Стьюдента . Оскільки > 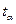і > 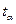, то гіпотези про відсутність тенденції як в середньому поточному значенні ряду, так і в дисперсії відхиляються, т.т. в цьому часовому ряду є тренд і тенденції в дисперсії ряду.

Розглянемо деякі теоретичні питання виявлення і фільтрації сезонної компоненти часового економічного ряду.

Під згладжуванням тренд-сезонного часового ряду розуміють процес отримання оцінок , а під фільтрацією компонент – процес отримання оцінок , , .

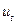Існують три основні напрями фільтрації компонент часового ряду виду (12.15): регресійні, спектральні і ітераційні.

Дата добавления: 2015-10-23