Программирование задач обработки одномерных массивов

Рассмотрим на примерах основные этапы решения задач обработки одномерных массивов.

Пример№1. Задан вектор vX из n элементов. Cоставить функцию пользователя для формирования нового вектора vY по следующим формулам:

I Математическое описание задачи

Дано: вектор vX={vX_i},

Основные зависимости, необходимые для решения задачи:

vY_i=vX_i-5 (1)

vY_i=vX_i+5 (2)

Ограничения:

Зависимость (1) выполняется, если vX_i>5;

Зависимость (2) выполняется, если vX_i£5;

Найти: вектор vY={vY_i}, .

II Схема алгоритма формирования нового вектора vY с краткими комментариями представлена на рис. 10.

Рекомендация! Количество элементов в векторе можно определить с помощью встроенной функции rows(имя вектора) или length(имя вектора).

 

Цикл вычисления элементов нового массива vY на основе исходного vX по заданным формулам, в зависимости от результатов проверки условия.

Определение количества элементов в исходном векторе с помощью встроенной функции rows()

Рис. 10. Схема алгоритма формирования
нового вектора vY

III Определение функции пользователя Fun_2V(vX) для формирования элементов нового массива. Fun_2V –имя функции (задано произвольно), vX - формальный параметр функции.

Листинг 1 с текстом функции пользователя.

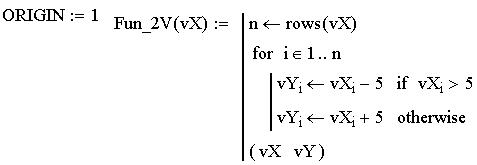
IV Вызов функции пользователя. Для проверки работы функции создадим с помощью шаблона вектор vA из 5-ти произвольных элементов:

Функция Fun_2V(vA) возвращает массив, элементами которого являются два вектора: исходный и результирующий (т.е., возвращает массив массивов).

Ответ в виде ({5,1} {5,1}) означает вывод двух массивов, каждый из которых содержит 5 строк и 1 столбец. Чтобы отобразить содержимое этих массивов достаточно выполнить двойной щелчок мыши в правой части оператора вывода и в появившемся диалоговом окне Формат Результата на закладке Параметры экрана включить опцию Развернуть вложенные массивы.

В ряде случаев целесообразно объединить возвращаемые массивы, представив их в виде матрицы. В листинге 2 представлен второй вариант программного блока для формирования нового вектора, отличающийся от предыдущего только последней строкой. В последней строке используется функция аugment(vX,vY), с помощью которой два вектора будут объединены в матрицу. В этом случае при обращении к функции Fun_2V(vA) будет выведена матрица, в первом столбце которой находится исходный вектор, а во втором – результирующий.

Листинг 2 с текстом функции пользователя.

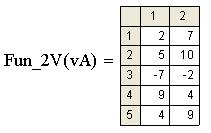
Пример№2. В массиве целых чисел vA={vA_i}, i= вычислить количество чётных, положительных элементов. Если в массиве таких элементов не окажется, то вывести об этом сообщение Исходный массив создать на интервале [-10,10] с помощью встроенной функции для генерации случайных чисел. Количество элементов в массиве n задать произвольно.

I Математическое описание задачи

Дано: n, {vA_i},i=

Основные зависимости:

к=к+1 (1)

Ограничения:

зависимость (1) выполняется, если i-й элемент массива vA_i >0 и четный;

если в массиве не окажется четных положительных элементов, то вывести об этом сообщение.

Найти: к.

Рекомендация: Для проверки четности элемента можно использовать встроенную функцию mod(x, y). Эта функция возвращает остаток от деления x на y. Результат имеет один знак с x.

II Схема алгоритма представлена на рис. 11.

Рис. 11. Схема алгоритма

III Листинг 3 с текстом функции пользователя

IV Вызов функции пользователя. Для проверки работы функции Fun_Count() сначала создадим вектор vC из 15-ти элементов на интервале [-10, 10], а затем обратимся к функции Fun_Count с фактическим параметром vC.

- Создание вектора vC:

- Вызов функции с Fun_Count(vC)

В созданном векторе оказалось 4 элемента, которые удовлетворяют заданному условию.

При повторном обращении к функции runif() будут получены другие значения вектора vC.

- Создание вектора vC:

- Вызов функции с Fun_Count(vC):

В созданном массиве не оказалось элементов, удовлетворяющих заданному условию.

Содержание отчета по лабораторной работе

1. Тема и цель лабораторной работы;

2. Условия задач, выданные преподавателем;

3. Математическое описание задач.

4. Схемы алгоритмов.

5. Записи функций пользователя с текстом программ.

6. Листинги с текстом программ (с комментариями) и результатами выполнения.

7. Анализ результатов.

Контрольные вопросы.

1. Какие типовые алгоритмы используются при обработке массивов?

2. Как подсчитать сумму (произведение) всех элементов массива?

3. Как подсчитать сумму (произведение) особых элементов массива?

4. Какой принцип используется при подсчете количества особых элементов массива?

5. Как организуется вычисление среднего арифметического элементов массива?

6. Как организуется вычисление среднего геометрического элементов массива?

7. На каком принципе основан поиск максимального (минимального) элементов массива?

8. На каком принципе основан поиск максимального (минимального) среди особых элементов массива?

9. Назначение встроенной функции mod(x,y).

10. Использование встроенной функции mod(x,y) для проверки кратности чисел.

11. Назначение встроенной функции rnd(X).

12. Назначение встроенной функции runif(n,a,b).

13. Отличие в использовании функций rnd() и runif().

14. Назначение встроенной функции trunc(х).

15. Назначение встроенной функции round(х).

16. Назначение встроенной функции floor(х).

17. Назначение встроенной функции ceil().

Для справки:

Функции для получения псевдослучайных чисел:

- функция rnd(x) возвращает универсальное случайное вещественное число на интервале от 0 до х; для получения случайного вещественного числа на интервале от a до b используется обращение к функции в виде: a+rnd(b-a);

- функция runif(n,a,b) возвращает вектор из n вещественных случайных чисел с универсальным распределением на интервале от a до b.

Для получения целочисленных случайных чисел достаточно к результату, возвращаемому функцией rnd(x) или runif(n,a,b) применить одну из функций округления.

Функции для округления вещественного числа:

1. trunc(х) - возвращает целую часть вещественного числа х;

2. round(х) - возвращает число, округленное до ближайшего целого;

3. floor(х) - возвращает наибольшее целое, меньшее или равное х;

4. ceil() - возвращает наименьшее целое, большее или равное х.

Примеры создания векторов с помощью функций для генерации случайных чисел:

- с помощью функции rnd():

a)вектор vB из 25 вещественных чисел на интервале от -5 до 15:

i:=1,2..25 vB_i:=-5+rnd(21);

b) - вектор vX из 50 целых чисел на интервале [20,35]

i:=1,2..50 vB_i:=20+round(rnd(16));

c) – вектора из 45-ти вещественных и целых чисел на интервале от -4 до 4. Ниже приведены первые 10 элементов созданных массивов.

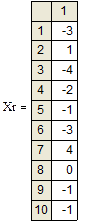
Функции rows() или length() используются для определения количества элементов в векторе.

Функция mod(x, y) возвращает остаток от деления x на y. Результат имеет один знак с x. Эта функция может быть использована для проверки кратности числа х числу y.

Функция concat(S1, S2, S3, …) возвращает строку, образованную присоединением строки S2 к концу строки S1, строки S3 к концу строки S2 и т.д.

Функция num2str(x) возвращает строку, символы которой соответствуют десятичному числу х.

Дата добавления: 2015-10-30