Основные алгоритмы обработки одномерных массивов

Порядок выполнения работы

1. Изучение типовых алгоритмов обработки одномерных массивов.

2. Изучение правил разработки схем типовых алгоритмов обработки одномерных массивов.

3. Изучение приёмов перехода от схемы алгоритма к программе.

4. Разработка математического описания, схемы алгоритма и программы для задач, выданных преподавателем.

Краткие теоретические сведения.

Основные алгоритмы обработки одномерных массивов

В данной лабораторной работе рассматриваются следующие типовые алгоритмы обработки одномерных массивов:

- формирование элементов массива по заданным формулам;

- накопление суммы всех элементов массива или суммы элементов массива удовлетворяющих заданному условию;

- накопление произведения всех элементов массива или произведения элементов массива удовлетворяющих заданному условию;

- вычисление количества элементов массива, удовлетворяющих заданному условию;

- вычисление среднего значения (среднего арифметического и среднего геометрического) элементов массива а также среднего значения элементов массива, удовлетворяющих заданному условию;

- нахождение минимального (максимального) элемента массива и его порядкового номера (индекса).

Напомним, что массивом называется упорядоченная последовательность данных, обозначенная одним именем. Положение конкретного элемента массива определяется его порядковым номером (индексом). Начальное значение индекса в массиве зависит от системной переменной ORIGIN. По умолчанию ORIGIN=0, но, по желанию пользователя, этой переменной можно присвоить любое целое число (положительное или отрицательное).

Обработка массивов осуществляется с использованием циклического алгоритма, так как над каждым элементом массива, как правило, выполняются однотипные операции. Обычно в качестве переменной цикла выступает номер (индекс) элемента массива, принимающий последовательно все значения, начиная с номера первого элемента до номера последнего элемента массива с шагом единица. Ниже приведено краткое описание типовых алгоритмов с примерами блок-схем для обработки некоторого исходного массива X из n элементов. Для определенности примем начало отсчета индекса с единицы, т.е. ORIGIN=1.

1.1 Формирование элементов нового массива по заданным формулам. Пусть задан массив {X_i}, i= . Сформировать n элементов нового массива Y по формулам:

Пример схемы алгоритма формирования нового массива показан на рис. 1.

Рис.1.Пример схемы алгоритма формирования нового массива.

Здесь по переменной i (индексу элемента массива) организован цикл, который будет выполняться n раз. При каждом выполнении тела цикла вычисляется элемент массива Y_i по одной из двух заданных формул в зависимости от проверяемого условия.

1.2 Накопление суммы элементов массива .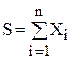

Задача сводится к организации цикла, в котором будет накапливаться сумма элементов массива путем прибавления текущего значения X_i к сумме предыдущих по формуле S=S+X_i (рис. 2). Начальному значению суммы S перед выполнением цикла следует присвоить значение ноль.

Рис. 2. Пример схемы алгоритма накопления суммы элементов массива.

Рис. 3. Пример схемы алгоритма накопления суммы элементов Xi >5.

Если нужно вычислить сумму только тех элементов массива, которые удовлетворяют заданному условию, то накопление суммы должно выполняться в случае истинности проверяемого условия (рис. 3).

1.3 Накопление произведения элементов массива . Задача сводится к организации цикла, в котором будет накапливаться произведение элементов массива путем умножения текущего значения X_i на произведение предыдущих по формуле P=P*X_i (рис. 4). Начальному значению переменной P перед началом цикла следует присвоить значение единица. Для вычисления произведения элементов массива, удовлетворяющих заданному условию, необходимо предварительно проанализировать истинность проверяемого условия (рис. 5).

Рис. 4. Пример схемы алгоритма накопления произведения элементов массива.

Рис. 5. Пример схемы алгоритма накопления произведения элементов Xi >5.

1.4 Вычисление количества элементов массива, удовлетворяющих заданному условию. Задача сводится к организации цикла, в котором будет анализироваться каждый элемент массива и, в случае выполнения заданного условия, накапливаться их количество путем прибавления единицы. Начальному значению количества перед началом цикла следует присвоить значение ноль. На рис. 6 приведена схема алгоритма для подсчета количества элементов массива Х_i, для которых выполняется условие: Х_i>5.

Рис. 6. Пример схемы алгоритма вычисления количества элементов X_i>5.  

1.5 Вычисление среднего арифметического элементов массива, удовлетворяющих заданному условию. Для этого в цикле анализируется каждый элемент массива и, в случае выполнения заданного условия, накапливаться их сумма путем прибавления выбранного элемента к сумме предыдущих и количество путем прибавления единицы. Начальному значению суммы и количества перед началом цикла следует присвоить значение ноль. После завершения цикла вычисляется среднее значение по формуле 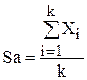, где k – количество элементов массива, удовлетворяющих заданному условию (рис. 7).

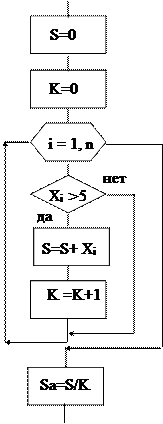Рис. 7. Пример схемы алгоритма вычисления среднего арифметического элементов X_i>5  

Для вычисления среднего геометрического элементов массива следует организовать цикл, в котором будет накапливаться произведение и количество элементов массива, удовлетворяющих заданному условию. Значение среднего геометрического вычисляется после завершения цикла по формуле .

1.6 Нахождение максимального (минимального) элемента массива и его порядкового номера (индекса).

Рассмотрим алгоритм нахождения в массиве Х максимального элемента и его номера. Введем обозначения: Мах – имя переменной для хранения максимального элемента массива, nMax – имя переменной для хранения индекса максимального элемента. Предварительно (условно) в качестве стартового значения переменной Мах присвоим значение первого элемента массива (Х₁), а переменной nMax - его номер (1). Нахождение максимального элемента выполняется в цикле. Алгоритм основан на сравнении текущего i-го элемента массива Х_i со значением переменной Мах. Если значение очередного элемента массива Х_i окажется больше значения Мах, то это значение следует считать максимальным, а его индекс – номером максимального элемента. В противном случае переменные Мах и nMax сохраняют прежние значения.Схема алгоритма приведена на рис. 8.

В ряде случаев требуется определить максимальный (минимальный) элемент среди особых элементов массива, т.е. среди элементов, удовлетворяющих некоторому заданному условию. Данный алгоритм во многом аналогичен алгоритму, приведенному выше, только перед началом цикла в ячейку для хранения значения искомого максимального (минимального) элемента рекомендуется записать значение, заведомо не являющееся максимальным (минимальным) для данного массива, а в ячейку для хранения номера искомого элемента - значение ноль.В цикле следует дополнительно проверять удовлетворяет ли текущий i-й элемент массива Х_i заданному условию. Пример схемы алгоритма поиска в массиве максимального положительного элемента и его порядкового номера приведен на рис. 9.

Дата добавления: 2015-10-30