Теория вероятности и математическая статистика

1. Монету бросают 4 раза. Найти вероятность того, что герб выпадет

- хотя бы 1 раз

- более 1-го раза и менее 4-х раз.

Решение.

Вероятность выпадения герба при одном броске р=0,5, орла q=0.5

Вероятность того, что герб появится хотя бы один раз, найдем по формуле

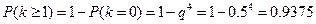
Вероятность того, что герб появится более 1 раза и менее 4-х раз

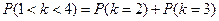
Воспользуемся формулой Бернулли

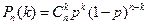
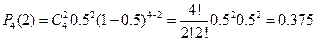
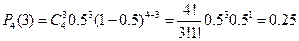
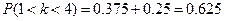
Ответ: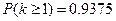

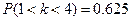
1. Из букв разрезной азбуки составлено слово «вероятность». Ребенок, не умеющий читать, рассыпал эти буквы и затем часть их собрал в произвольном порядке. Найти вероятность того, что

- буква «о» появится раньше «р»

- у него получится слово «верность».

Решение.

вероятность того, что буква «о» появиться раньше буквы «р».

Данные событие может произойти если буква о будет первой или впереди буквы «о» будет стоять любая буква кроме «р».

Обозначим А- событие, состоящее в том, что буква «о» появиться раньше «р»

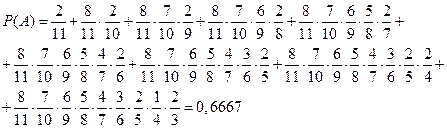
Найдем вероятность того, что получиться слово «верность».

Ответ: а)p=0.6667 б)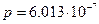

1. Группа студентов состоит из 5 отличников, 10 хорошо успевающих, 5 занимающихся слабо. Отличники на экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад два студента. Найти вероятность того, что

- среди них окажется хотя бы один слабый студент

- были вызваны два хороших студента, если они получили две хорошие оценки.

Решение.

Для нахождения вероятности того, что среди двух вызванных студентов хотя бы один будет слабым воспользуемся классическим определением вероятности

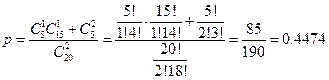
Найдем вероятность того, что вызванный студент получит хорошую оценку, для этого воспользуемся формулой полной вероятности

Обозначим А- событие состоящее в том, что студент получит хорошую оценку.

Можно выдвинуть шесть гипотез

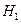- вызвали два слабых ученика

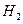- вызвали слабого и хорошего учеников

- вызвали слабого и отличника учеников

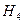- вызвали два хороших ученика

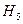- вызвали хорошего и отличник учеников

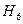- вызвали два отличника

Вероятности гипотез

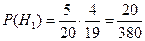
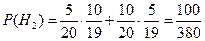
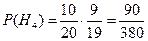
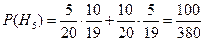
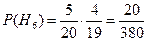
Условная вероятность того, что оба ученика получат хорошие оценки

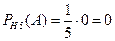
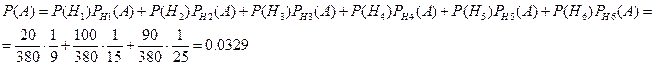
Вероятность того, что два студента получивших хорошие оценки являются хорошистами найдем, воспользовавшись формулой Байеса

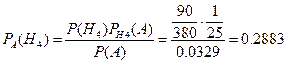
Ответ: а) 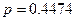б)

1. 90% всех студентов сдают сессию с первого раза. Найти математическое ожидание и стандартное отклонение числа студентов, сдавших сессию с первого раза, из выбранных наугад четырех. Найти функцию распределения указанной случайной величины и построить ее график.

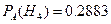
Решение.

Так как случайная величина Х – число студентов сдавших на отлично с первого раза подчиняется биномиальному закону, то математическое ожидание найдем по формуле

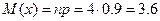
Для нахождения функции распределения найдем вероятности каждого значения Х. для этого воспользуемся формулой Бернулли

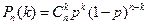
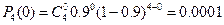
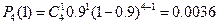
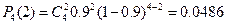
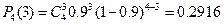
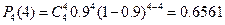
Функция распределения

1. Рост мужчины в некоторой местности является случайной величиной, распределенной по нормальному закону с дисперсией, равной 49 см². Считая, что средний рост равен 170 см, найти вероятность того что наугад выбранный мужчина будет иметь рост

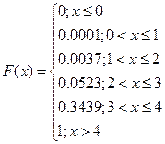
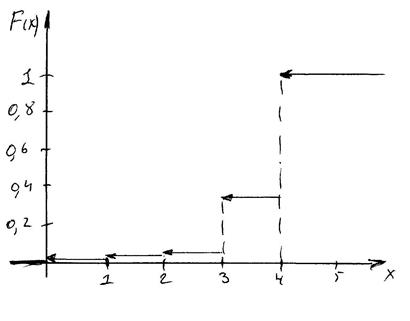
- от 172 до 177 см

- менее 172 см

Решение.

Так как случайная величина Х распределена по нормальному закону, то вероятность того, что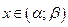

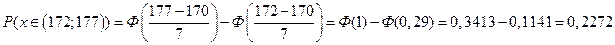
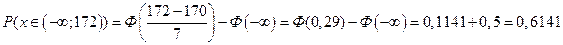
Ответ: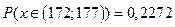

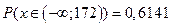
№6

1. Параметр а найдем. Воспользовавшись свойством вероятности

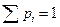
0,1+a+0,2+0,05+0,15+0,2=1

a=0.3

2. Составим ряд распределения Х

x
p	0,15	0,45	0,4

Полигон распределения

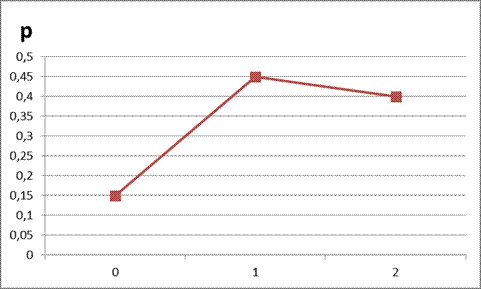
3. Вероятность того, что x<1

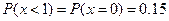
Вероятность того, что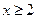

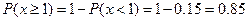
4. Среднее значение CВ х

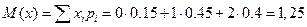
5. математическое ожидание

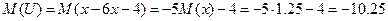
6. Степень разбросанности CВ Х

Найдем коэффициент вариации

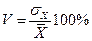
Где среднее квадратическое отклонение

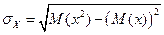
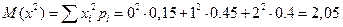
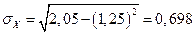
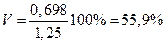
6. Дисперсия

8. Ковариация

.

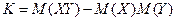
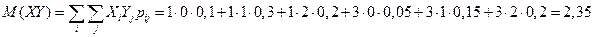
Отрицательная ковариация означает, что связь между признаками обратная.

9. коэффициент корреляции

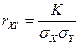
Среднее квадратическое отклонение Y

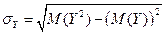
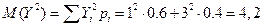
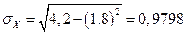
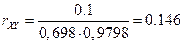
Коэффициент корреляции не может равняться 3, так как он может лежать в интервале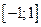

10. Случайная величина V=-5+3x

Составим ряд распределения СВ V

V	-5	-2
p	0,15	0,45	0,4

Математическое ожидание найдем, воспользовавшись свойством математического ожидания

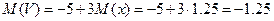
Среднее квадратическое отклонение найдем воспользовавшись свойством среднего квадратического отклонения

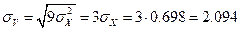
Ковариация

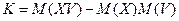
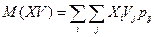
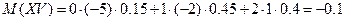
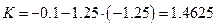
Коэффициент корреляции

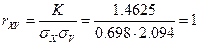
7. Данные о месячной заработной плате 25 случайно отобранных рабочих завода приведены в таблице

Зарплата, ден.ед	500-550	550-600	600-650	650-700	700-750
Число рабочих

Вычислите выборочную среднюю зарплату и несмещенную оценку стандартного отклонения.

Решение.

Выборочную среднюю зарплату найдем по формуле

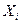- середина i-го интервала

лен. Ед.

Несмещенную оценку стандартного отклонения найдем по формуле

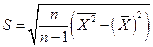
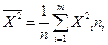
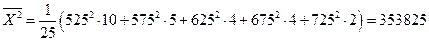
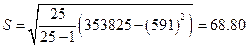ден. Ед.

Ответ: 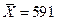лен. Ед. 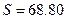ден. Ед.

При опросе 150 человек 5 оказались безработными. С надежностью 0,95 оценить процент безработных в городе. Сколько человек нужно опросить, чтобы с вероятностью 0,95 можно бы­ло утверждать, что доля всех безработных отличается от истинной не более чем на 0,2?

Решение.

Дата добавления: 2015-10-23