Однородные и неопределённые системы линейных алгебраических уравнений.

Support К лабораторной работе № 5.

Задание 1. Проверить неоднородную СЛАУ на совместность и, если система совместная, выяснить определённая она или неопределённая (с помощью критерия Кронекера – Капелли).

Найти общее решение системы, два частных решения и все базисные решения.

Решение. Составим матрицу системы и расширенную матрицу и приведём их к ступенчатой форме с помощью элементарных преобразований матриц:

Так как 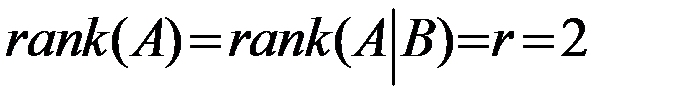, то по критерию Кронекера-Капелли система совместна, а из неравенства 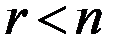( - количество неизвестных) следует, что система уравнений неопределённая и имеет бесконечно много решений.

Найдём общее решение системы. По ступенчатой матрице составим систему уравнений, равносильную данной:

Выберем в качестве базисного минор

.

Тогда неизвестные будут базисными, а неизвестные 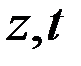- свободными. В системе уравнений 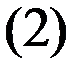базисные неизвестные оставим в левой части, а свободные перенесём в правую:

Решим эту систему, придавая свободным переменным произвольные действительные значения: :

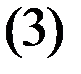
является общим решением системы уравнений , где - произвольные действительные числа.

Множество всех решений системы является подмножеством линейного пространства : ( называется мерным арифметическим пространством).

Придавая в 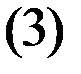определённые значения будем получать частные решения системы . Например, при получим частное решение .

Решение системы , в котором все свободные неизвестные равны нулю, называется базисным.

, - базисное решение.

Задание 2. Выяснить, является ли однородная система, соответствующая данной,неопределённой или определённой(имеет нетривиальные решения или только тривиальное).

Для неопределённой однородной системы найти общее решение, фундаментальную систему решений, разложить общее решение по фундаментальной системе.

Решение. Рассмотрим однородную систему уравнений, соответствующую данной

Как и в Задании 1 матрицу системы приведём их к ступенчатой форме

(воспользуемся результатами, полученными при выполнении Задания 1).

По ступенчатой матрице составим однородную систему уравнений, равносильную данной:

Так как 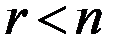( - ранг матрицы системы , - количество неизвестных), то система неопределённая и имеет нетривиальные решения (бесконечно много решений).

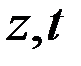Вновь выберем неизвестные базисными, а неизвестные - свободными. В системе уравнений базисные неизвестные оставим в левой части, а свободные перенесём в правую и решим систему относительно базисных неизвестных:

является общим решением однородной системы уравнений , где принимают любые действительные значения.

Множество

всех решений однородной системы является подмножеством линейного пространства : . Как известно само является линейным пространством относительно операций сложения решений и умножения решений на действительное число. Поэтому является подпространством пространства . Размерность равна : , где - ранг матрицы системы . Это означает, что базис пространства (он всегда существует) состоит из (двух) векторов и . Эти вектора, записанные в форме матриц – столбцов, принадлежат и сами являются решениями однородной системы . Эта система вектор - столбцов является базисом в и называется фундаментальной системой решений однородной СЛАУ .

Общее решение однородной СЛАУ может быть однозначно представлено линейной комбинацией решений фундаментальной системы:

,

где , где - произвольные постоянные.

Решения фундаментальной системы(базисные векторы) могут быть получены, если поочерёдно одной свободной неизвестной придавать значение 1, а всем остальным свободным- нули:

Значения неизвестных
Базисные
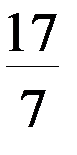
Свободные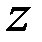

Ответ: общее решение однородной системы уравнений

,

т.е.

Дата добавления: 2015-10-30