
Читайте также:
|
Наиболее часто используемый метод численного интегрирования основан на замене подынтегральной функции интерполированной, как правило, не выше квадратичной.
Пусть требуется вычислить интеграл
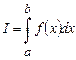
от функции, заданной на [a, b] значениями f0, f1, …, fn в n узловых точках x0, x1, …, xn.
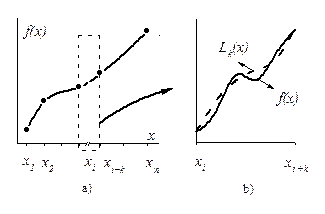
|
Рис. 1
Разобьем [a, b] на m отрезков, которые могут содержать несколько узлов (рис.1a). Тогда
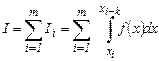
На каждом отрезке [xi, xi+k ], содержащем k узлов, составляем интерполяционный многочлен Lk(x) (рис. 1b), и, заменяя подынтегральную функцию f(x)» Lk(x), получим
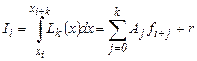 (1)
(1)
где Aj – коэффициенты, зависящие только от выбора узлов, но не от функции f, r – погрешность. Суммируя выражения (1) по всем отрезкам, получаем квадратурную формулу:
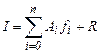
Здесь R – погрешность квадратурной формулы. Рассмотрим некоторые простые квадратурные формулы на равномерной сетке с шагом h = xi+1 – xi = const.
1. Формулы прямоугольников.
Простейшие формулы получаются в том случае, когда в качестве интерполирующей функции берется константа (интерполирование проводится по одной точке). В данном случае функция f(x) заменяется ступенчатой функцией (рис. 2).
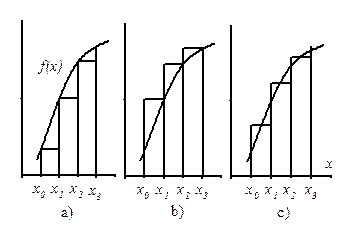
|
Рис. 2
Если интерполяция проводится по левой или правой точке отрезка [xi, xi+1 ], то квадратурные формулы имеют вид соответственно (рис. 2a, b):
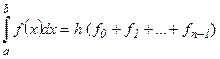 (2)
(2)
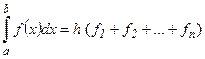 (3)
(3)
где h = (b – a)/n.
Формула средних. Если в качестве интерполирующей точки выбирается средняя точка между xi и xi+1 (рис. 2с), то
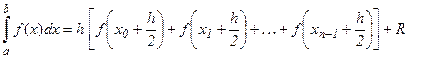 (4) где погрешность равна
(4) где погрешность равна
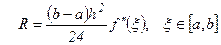 (5)
(5)
Формула средних дает точное значение интеграла, если подынтегральная функция линейна.
2. Формула трапеций.
Интерполирование исходной функции по двум точкам в промежутке [xi, xi+1 ] между соседними узлами приводит к замене f(x) отрезком прямой, а на отрезке [a, b] – ломаной кривой (рис. 3). На равномерной сетке интеграл по формуле трапеций равен
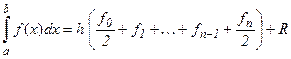 (6)
(6)
Погрешность формулы трапеций.
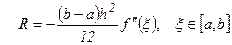 (7)
(7)
Формула трапеций является точной для линейной функции f(x), однако, в данном случае погрешность вдвое выше, чем погрешность формулы средних.
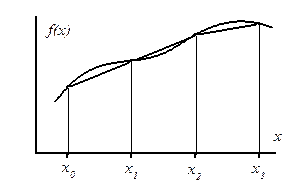
|
Рис. 3
3. Формула Симпсона.
Квадратурная формула Симпсона на равномерной сетке имеет вид:
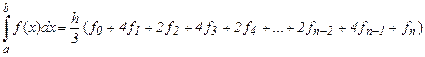 (8)
(8)
где шаг равен
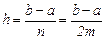
Здесь интерполяция проводится квадратичным многочленом по трем соседним узлам xi, xi+1, xi+2, вследствие этого общее разбиение отрезка должно быть таким, чтобы n = 2m было четным.
Погрешность формулы Симпсона равна
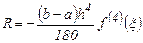 (9)
(9)
Формула Симпсона является точной для подынтегральных функций, являющихся многочленами до третьей степени включительно.
Пример 1. Вычислить интеграл по формуле трапеций (n = 10) и формуле Симпсона (n = 10) и оценить погрешность вычислений, где n – количество отрезков, на которые разбивается отрезок интегрирования.
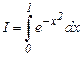
Решение. Максимальные погрешности формул трапеций и Симпсона равны соответственно

где 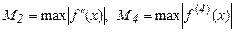 .
.
Для функции
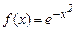
имеем
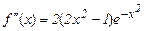
Третья производная 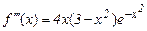 на отрезке [0,1] положительна, т.е.
на отрезке [0,1] положительна, т.е. 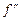 – возрастающая функция. Следовательно,|
– возрастающая функция. Следовательно,| 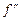 |достигаетнаибольшего значения на краях интервала, в данном случае
|достигаетнаибольшего значения на краях интервала, в данном случае
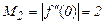
Погрешность формулы трапеций равна
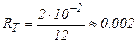
Четвертая производная f равна
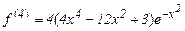
Экстремумы этой функции, т.е. нули функции
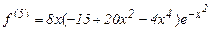
лежат вне интервала (0,1). Легко проверить, что M4 = f(4)(0) = 12. Отсюда
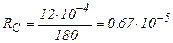
В соответствии с оценками погрешности находим, что в значении интеграла, вычисленным по методу трапеций третий знак после запятой является сомнительным, а по формуле Симпсона число правильных знаков после запятой не превышает пяти. Вычисление функций в узлах проводим с двумя запасными знаками (шесть знаков после запятой).
| i | ||||||
| xi | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| fi | 0.990050 | 0.960789 | 0.913931 | 0.852144 | 0.778801 |
| i | |||||
| xi | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| fi | 0.697676 | 0.612626 | 0.527292 | 0.444858 | 0.367879 |
Вычисление по формуле трапеций (6) с данными из таблицы дает значение интеграла I = 0.7462106, однако с учетом погрешности | R | < 0.002 значение интеграла следует положить равным I = 0.746.
Аналогичные вычисления по формуле Симпсона (8) дают значение интеграла I = 0.7468248. Поскольку погрешность в данном случае составляет | R | < 0.67×10 - 5, то интеграл равен I = 0.74682.
4. Выбор шага интегрирования по оценке остаточного члена.
В подобных задачах требуется определить шаг сетки, который обеспечивает требуемую точность e вычисления интеграла по выбранной квадратурной формуле. Шаг выбирается из условия равенства максимальной погрешности Rmax и заданной точности для данной формулы численного интегрирования
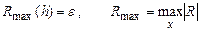 (10)
(10)
где остаточный член R определяется одним из условий (5), (7), (9) соответствующей квадратурной формулы. Тогда для формулы средних (прямоугольников), трапеций и Симпсона получаем следующие выражения Rmax, соответственно:
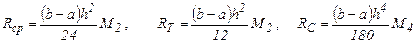 (11)
(11)
где 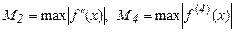 .
.
Пример 2. Вычислить интеграл
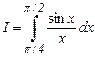
по формуле трапеций с точностью e = 10 - 4, определяя шаг h по оценке остаточного члена.
Решение. Величину шага интегрирования определим из соотношения (10) с максимальной погрешностью RT, соответствующей формуле трапеций.
Для функции

имеем
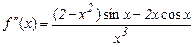
Используя представления в виде отрезка ряда

можем записать
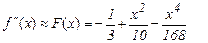
Экстремумы функции F(x) лежат за пределами 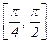 . Так как
. Так как 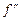 (p/2) = - 0.121 и
(p/2) = - 0.121 и 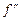 (p/4) = - 0.274,то M2 = 0.274.
(p/4) = - 0.274,то M2 = 0.274.
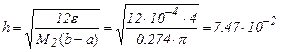
В результате (b-a)/h = 10.5, и следовательно интервал интегрирования следует разбить на n = 11 отрезков.
Составляем таблицу значений функции в узлах с шагом h = p /44.
| i | ||||||
| xi | 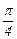
| 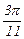
| 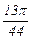
| 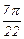
| 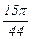
| 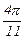
|
| fi | 0.900316 | 0.882063 | 0.862468 | 0.841592 | 0.819497 | 0.796248 |
| i | ||||||
| xi | 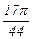
| 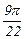
| 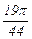
| 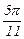
| 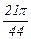
| 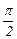
|
| fi | 0.771916 | 0.746573 | 0.720293 | 0.693154 | 0.665236 | 0.636620 |
Вычисление по формуле (6) с данными из таблицы дает значение интеграла I = 0.611719. Поскольку заданная точность может приводить к погрешности в четвертом знаке результата, то в ответе следует удержать 4 знака I = 0.6117.
5. Процедура двойного пересчета (правило Рунге).
Оценка максимальной погрешности Rmax часто связана с выполнением громоздких вычислений, поэтому на практике используется процедура двойного пересчета. Величина интеграла I рассчитывается сначала с шагом h (n интервалов), затем на сетке с вдвое меньшим шагом h/2 (2n интервалов). Здесь роль погрешности метода вычислений играет величина
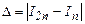 (12)
(12)
Более точные оценки погрешности дают формулы Рунге для выбранной квадратурной формулы:
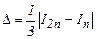 (13)
(13)
для формулы средних и трапеций
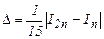 (14)
(14)
для формулы Симпсона.
Если D не превосходит заданной погрешности e, т.е. D < e, то вычисления прекращают и полагают
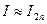 .
.
Если точность не достигается, то процедуру уменьшения шага повторяют вновь.
Поскольку в данном случае априорная погрешность метода неизвестна, то невозможно использовать выражения (11). Однако, согласно этим соотношениям погрешность имеет вид для формулы средних и трапеций R = a h2, а для формулы Симпсона R = a h4, где a и b – константы. Следовательно, шаг определяется соотношением h = const 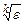 , где k = 2 или k = 4 в зависимости от метода вычисления. На практике константу полагают равной единице, и в качестве начального шага выбирается величина
, где k = 2 или k = 4 в зависимости от метода вычисления. На практике константу полагают равной единице, и в качестве начального шага выбирается величина 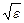 для формул трапеций и средних, и
для формул трапеций и средних, и 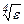 для формулы Симпсона. Если точность вычисления интеграла невысока, то в качестве начальной сетки выбирают разбиение на 8 – 10 отрезков.
для формулы Симпсона. Если точность вычисления интеграла невысока, то в качестве начальной сетки выбирают разбиение на 8 – 10 отрезков.
Пример 3. Используя процедуру двойного пересчета, вычислить по формуле Симпсона интеграл
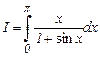
с точностью e = 2×10 - 4.
Решение. Вначале отрезок интегрирования разбиваем на 8 частей и вычисляем интеграл при h = p/8. Значения аргументов и подынтегральной функции приведены в таблице:
| i | |||||||||
| xi | 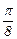
| 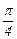
| 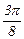
| 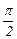
| 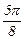
| 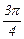
| 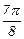
| p | |
| fi | 0.284012 | 0.460075 | 0.612355 | 0.785398 | 1.020591 | 1.380226 | 1.988086 | p |
По формуле Симпсона вычисляем значение интеграла при h = p/8 (n=8):
I8 = 3.143317
Из этой же таблицы находим значение интеграла при h = p/4 (n=4):
I4 = 3.160861
По формуле (12) находим, что разность
| I8 –I4| = 0.016 > e = 2×10 - 4
Погрешность D, вычисленная по формуле Рунге (14), также превышает e. Поэтому вычисления следует выполнить с вдвое меньшим шагом h = p /16 (n=16). Результаты вычисления аргумента и функции сводим в следующую таблицу:
| i | ||||||||
| xi | 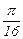
| 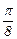
| 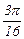
| 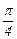
| 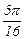
| 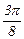
| 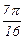
| |
| fi | 0.164296 | 0.284012 | 0.378671 | 0.460075 | 0.536043 | 0.612355 | 0.693889 |
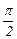
| 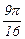
| 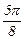
| 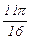
| 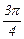
| 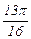
| 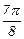
| 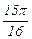
| p |
| 0.785398 | 0.892144 | 1.020591 | 1.179296 | 1.380226 | 1.640905 | 1.988086 | 2.464452 | p |
Значение интеграла, вычисленное по этой таблице равно
I16 = 3.141716
Разность | I16 –I8| = 0.0016. Согласно соотношению (14) погрешность
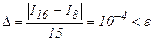
Следовательно, значение интеграла I = I16 =3.1417.
6. Интегрирование с помощью степенных рядов.
Пусть подынтегральная функция f(x) разлагается в степенной ряд
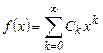
сходящийся в интервале – R £ x £ R, который содержит отрезок интегрирования [ a, b ]. Тогда интеграл можно почленно проинтегрировать
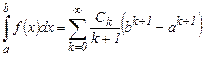
Если ряд сходится быстро, то его можно заменить частной суммой
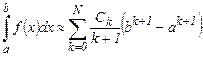
В данном случае, погрешность складывается из погрешности округления членов суммы и погрешности обрезания ряда, равной остатку ряда.
Для знакопеременного ряда абсолютная величина остатка ряда не превосходит абсолютной величины первого отброшенного члена ряда. В других случаях используют мажорантные оценки известными рядами.
Пример 4. Вычислить интеграл
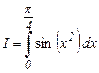
с точностью e = 10 - 4 путем разложения подынтегральной функции в ряд. Оценить количество слагаемых в приближенном выражении интеграла по формуле трапеций с той же точностью
Решение. Для функции 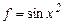 имеем разложение
имеем разложение
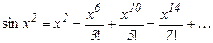
Интегрирование почленно дает
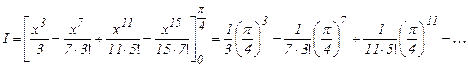 Поскольку ряд знакопеременный, то достаточно удержать столько членов, чтобы первый отброшенный был менее 10 - 4. Этому условию удовлетворяет третье слагаемое, поскольку
Поскольку ряд знакопеременный, то достаточно удержать столько членов, чтобы первый отброшенный был менее 10 - 4. Этому условию удовлетворяет третье слагаемое, поскольку
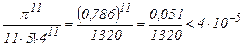
Следовательно, интеграл равен
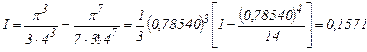
Погрешность формулы трапеций определяется формулой (11). Максимум функции 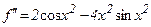 находим из условия экстремума
находим из условия экстремума
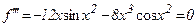
Решение уравнения
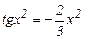
имеет единственное решение x=0 и оно соответствует максимуму 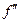 . По формуле (11) находим
. По формуле (11) находим
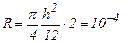
Следовательно, шаг 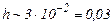 , т.е. для достижения указанной точности по формуле трапеций следует взять около 30 слагаемых.
, т.е. для достижения указанной точности по формуле трапеций следует взять около 30 слагаемых.
Задачи.
1. Определить погрешность формул прямоугольников (2) и (3).
2. Вычислить интегралы по формуле средних при n = 10, где n – количество отрезков, на которые разбивается отрезок интегрирования и оценить погрешность вычислений.
a) 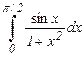 b)
b) 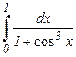
c) 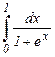 d)
d) 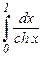
3. Вычислить интегралы по формуле трапеций (n = 10) и формуле Симпсона (n = 10) и оценить погрешность вычислений, где n – количество отрезков, на которые разбивается отрезок интегрирования.
a) 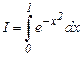 b)
b) 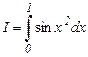 c)
c) 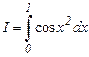
4. Вычислить интегралы по формуле трапеций с точностью e, определяя шаг h по оценке остаточного члена.
a) 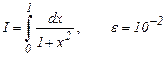 b)
b) 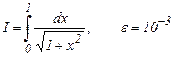 c)
c) 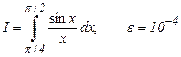
5. Вычислить интегралы по формуле Симпсона с точностью e = 10 – 3 используя процедуру двойного пересчета.
a) 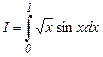 , b)
, b) 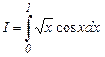 , c)
, c) 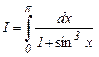
6. Вычислить интеграл с точностью e, разлагая подынтегральную функцию в степенной ряд.
a) 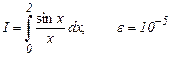 b)
b) 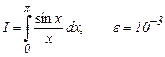 c)
c) 
7. Вычислить по формуле трапеций интеграл
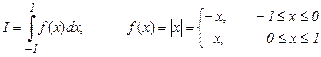 при четном и нечетном количестве узлов равномерной сетки.
при четном и нечетном количестве узлов равномерной сетки.
8. Каким образом следует выбрать узлы сетки, чтобы интеграл
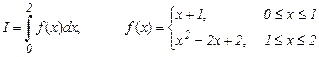
вычисленный по формуле Симпсона имел наименьшую погрешность.
9. Вычислить интеграл, заданный таблицей, и оценить погрешность:
| i | |||||||||
| xi | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 | 2.6 | |
| fi | 0.5 | 0.5455 | 0.5833 | 0.6154 | 0.6429 | 0.6667 | 0.6875 | 0.7059 | 0.7222 |
Ответы и указания.
3a). I = 0.746, | R | < 0.002; I = 0.74682, | R | < 0.67 10 -5
3b). I = 0.311, | R | < 1.9 10 -3; I = 0.3103, | R | < 1.6 10 -5
3c). I = 0.903, | R | < 3.2 10 -3; I = 0.9045, | R | < 1.3 10 –5
4a). I = 0.78 4b). I = 0.88137 4c). I = 0.6118
5a). I = 0.364 5b). I = 0.531 5c). I = 2.353
6a). I = 1.60543 6b). I = 1.852 6c). I = 0.7468
7). I = 1, n = 2k; I = 1+1/n2, n = 2k +1
8). Учесть, что формула Симпсона является точной для кубических для многочленов
Дата добавления: 2015-10-30; просмотров: 171 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определённый интеграл. | | | ИНТЕГРАЛЬНАЯ ЙОГА 1 страница |