
Читайте также:
|
Вариант 1
Часть1
1. Используя теорему существования определенного интеграла, установить, существует ли определенный интеграл от данной функции по указанному промежутку:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Используя одно из свойств определенного интеграла, упростите вычисление интеграла  .
.
3. Не вычисляя, определить, какой из интегралов больше:
а)  или
или  ; б)
; б)  или
или  . Ответ обосновать
. Ответ обосновать
4. Чему равны выражения:  и
и  , если f (t)- четная функция; нечетная функция?
, если f (t)- четная функция; нечетная функция?
5. Вычислить:
а)  б)
б) 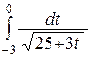 , в)
, в)  , г)
, г)  ;
;
д)  ; е)
; е) 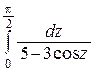 ; ж)
; ж)  ; з)
; з)  .
.
6. Вычислить  , если f (x) =
, если f (x) = 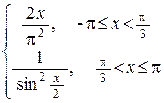 .
.
7. Вычислить интегралы, или установить их расходимость:
а)  , а > 0, б)
, а > 0, б) 
Часть 2
1. Построить фигуру, ограниченную линиями, и найти её площадь:
а) y = ln(x +1), y = 2, x = 0; б) r = 2j, j = a, j = b.
2. Найти длину дуги кривой: а)  ; б)
; б) 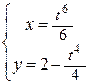 , где
, где  .
.
3. Найти объем тела, полученного вращением вокруг оси ОУ фигуры, ограниченной линиями  , у = 3, у = 12 и осью ОУ.
, у = 3, у = 12 и осью ОУ.
4. Скорость точки изменятся по закону  м/c. Найти путь, пройденный точкой за 6 секунд от начала движения.
м/c. Найти путь, пройденный точкой за 6 секунд от начала движения.
5. Определить давление воды на прямоугольный шлюз с основанием 18 м и высотой 6 м.
6. Вычислить работу, необходимую для растяжения пружины на 4 см, если известно, что от нагрузки в 1 Н она растягивается на 1 см.
Дополнительные задачи
1. Вычислить интеграл, рассматривая его как предел интегральной суммы:  .
.
2. Оценить интеграл  .
.
3. Исходя из геометрического смысла определенного интеграла, найти:
а)  ; б)
; б)  .
.
4. Исследовать сходимость интеграла  .
.
5.  Вычислить
Вычислить 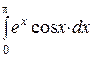 .
.
6. Найти значение Q, при котором S1 = S2 :
7. Найти длину спирали Архимеда r = a j, jÎ[0, 2p].
8. В цилиндрический стакан с водой вложен параболоид вращения вершиной вниз. Основание и высота параболоида совпадают с основанием и высотой цилиндра. Найти объем оставшейся в стакане воды, если радиус основания r, а высота h.
9. Найти статический момент окружности r = 2 a sinj относительно полярной оси.
Ответы. Часть 1: 1. а) нет; б) да; в) нет. 2. 0. 3. а)  >
>  ; б)
; б)  <
<  . 4.
. 4. 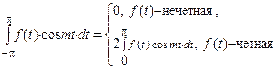 ,
,  . 5. а)190; б)
. 5. а)190; б)  ; в) 3; г)
; в) 3; г)  ; д) 2 а (3+ln4); е)
; д) 2 а (3+ln4); е)  ; ж)
; ж)  ; з) –2p. 6.
; з) –2p. 6.  7. а)
7. а) 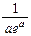 ; б) расходится.
; б) расходится.
Часть 2: 1. а) е 2–3; б)  . 2..
. 2..  ; б)
; б)  . 3. 4π. 4. 384 м. 5. 324ρg. 6.8дж
. 3. 4π. 4. 384 м. 5. 324ρg. 6.8дж
Вариант 2
Часть1
1. Используя теорему существования определенного интеграла, установить, существует ли определенный интеграл от данной функции по указанному промежутку:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Используя одно из свойств определенного интеграла, упростите вычисление интеграла  .
.
3. Не вычисляя, определить, какой из интегралов больше:
а)  или
или  ; б)
; б)  или
или  . Ответ обосновать
. Ответ обосновать
4. Чему равны выражения:  и
и 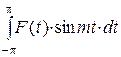 , если F (t)- четная функция; нечетная функция?
, если F (t)- четная функция; нечетная функция?
5. Вычислить:
а)  б)
б)  , в)
, в)  , г)
, г)  ;
;
д)  ; е)
; е) 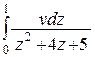 ; ж)
; ж)  ; з)
; з)  .
.
6. Вычислить  , если f (x) =
, если f (x) =  .
.
7. Вычислить интегралы, или установить их расходимость:
а)  б)
б)  , а > 0.
, а > 0.
Часть 2
1. Построить фигуру, ограниченную линиями, и найти её площадь:
а) y =1, y = 3, xy = a, х = 0 б)  .
.
2. Найти длину дуги кривой: а)  ; б)
; б)  , где
, где  .
.
3. Найти объем тела, ограниченного параболоидом вращения x =3(y 2 + z 2) и плоскостью x = 2.
4. Скорость тела изменятся по закону  м/c. Найти путь, пройденный телом за 1час и 20 мин от начала движения. Чему равна средняя скорость движения тела за этот промежуток времени?
м/c. Найти путь, пройденный телом за 1час и 20 мин от начала движения. Чему равна средняя скорость движения тела за этот промежуток времени?
5. В каком случае пластинка, погруженная в воду, испытывает большее давление (см. рисунок)?
6.  Материальная точка М движется по координатной прямой под действием силы, величина которой меняется пропорционально расстоянию точки от начала координат О. Известно, что направление силы совпадает с направлением оси, и, что она равнялась 1Н, когда расстояние МО было равно 3м. Вычислить работу этой силы по перемещению точки на расстояние 15 м от начала координат.
Материальная точка М движется по координатной прямой под действием силы, величина которой меняется пропорционально расстоянию точки от начала координат О. Известно, что направление силы совпадает с направлением оси, и, что она равнялась 1Н, когда расстояние МО было равно 3м. Вычислить работу этой силы по перемещению точки на расстояние 15 м от начала координат.
Дополнительные задачи
1. Вычислить интеграл  , рассматривая его как предел интегральной суммы.
, рассматривая его как предел интегральной суммы.
2. Оценить интеграл  .
.
3. Исходя из геометрического смысла определенного интеграла, найти:
а)  ; б)
; б)  .
.
4. Исследовать сходимость интеграла  .
.
5. Вычислить 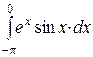 .
.
6. Найти площадь фигуры, ограниченной графиком функции  и касательной к графику функции
и касательной к графику функции  в точке (0;2).
в точке (0;2).
7. Найти длину кардиоиды  .
.
8. Криволинейная трапеция, ограниченная линиями 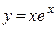 , x =1, y =0, вращается вокруг оси ОХ. Найти объем полученного тела.
, x =1, y =0, вращается вокруг оси ОХ. Найти объем полученного тела.
9. Найти моменты инерции эллипса  относительно обеих его осей.
относительно обеих его осей.
Ответы. Часть 1: 1. а) нет; б)нет; в) да. 2. 0. 3. а)  >
>  ; б))
; б))  <
<  .
.
4.  ,
, 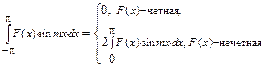 . 5. а)
. 5. а) 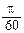 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) 3(12+4ln3); е)
; д) 3(12+4ln3); е)  ; ж)
; ж)  ; з)
; з)  .
.
6.  +
+  . 7. а) расходится; б)
. 7. а) расходится; б)  . Часть 2: 1. а) а ln3. б) 2 а 2. 2. а)
. Часть 2: 1. а) а ln3. б) 2 а 2. 2. а)  ; б) Т2/2.
; б) Т2/2.
3. 2π/3. 4.  5.Ра)>Рб). 6. 37,5 дж
5.Ра)>Рб). 6. 37,5 дж
ВАРИАНТ 3
Часть1
1. Используя теорему существования определенного интеграла, установить, существует ли определенный интеграл от данной функции по указанному промежутку:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Используя одно из свойств определенного интеграла, упростите вычисление интеграла  .
.
3. Не вычисляя, определить, какой из интегралов больше:
 а)
а)  или
или  ; б)
; б)  или
или  . Ответ обосновать.
. Ответ обосновать.
4. Чему равны выражения:  и
и  , если f (t)- четная функция; нечетная функция?
, если f (t)- четная функция; нечетная функция?
5. Вычислить:
а)  б)
б)  , в)
, в) 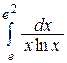 , г)
, г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
7. Вычислить  , если f (x) =
, если f (x) =  .
.
8. Вычислить интегралы, или установить их расходимость: а)  б)
б)  .
.
Часть 2
1. Построить фигуру, ограниченную линиями и найти ее площадь:
а) 
 , х = 0; б)
, х = 0; б)  .
.
2. Найти длину дуги линии:а)  ; б)
; б)  .
.
3. Найти объем тела, полученного вращением эллипса  вокруг его малой оси.
вокруг его малой оси.
4. Найти массу стержня длинною 100 м, если линейная плотность ρ меняется по закону  г/см, где х – расстояние от одного из концов стержня.
г/см, где х – расстояние от одного из концов стержня.
5. Найти силу, с которой жидкость удельного веса γ давит на вертикальную стенку, имеющую форму полуэллипса, большая ось которого находится на поверхности жидкости. Большая полуось эллипса а, малая ось b.
6. Пружина в спокойном состоянии имеет длину 0,2 м. Сила в 50 Н растягивает ее на 0,01 м. Какую работу нужно совершить, чтобы растянуть пружину от длины 0,22 м до длины 0,32 м?
Дата добавления: 2015-10-30; просмотров: 138 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дополнительные задачи | | | Дополнительные задачи |