Дополнительные задачи. 1. Доказать формулу Дирихле .Пользуясь этой формулой, доказать равенство .

1. Доказать формулу Дирихле .Пользуясь этой формулой, доказать равенство .

2. Какой из интегралов больше:

а)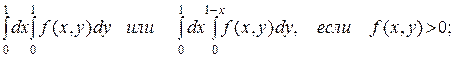

б) ?

3. Найти среднее значение функции z= 12-2 x -3 y в области, ограниченной прямыми 12-2 x -3 y =0, x =0, y =0. Отв. 4.

4. Оценить интеграл , где D – круг .
Отв.

5. Вычислить или установить его расходимость. Отв. 2.

6. Вычислить , если .
Отв. F(A,B)-F(A,b)-F(a,B)+F(a,b).

7. Вычислить . Отв. .

8. Найти объем тела, ограниченного цилиндрами и плоскостями z = 0, x+y = 2 e, 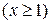. Отв. .

9. На тонкой пластине, имеющей форму параболического сегмента, ограниченного параболой и осью OX, распределён электрический заряд с поверхностной плотностью σ=2x+y. Найти полный заряд пластинки. Отв.

10. Плоское кольцо ограниченно двумя концентрическими окружностями, радиусы которых равны r и R, r<R. Зная, что плотность материала обратно пропорциональна расстоянию от центра окружностей, найти массу кольца. Плотность на внутренней окружности кольца равна единице. Отв. 2 πr(R-r).

11. В квадратной пластинке со стороной 3 плотность пропорциональна расстоянию от одной из её вершин. Найти среднее значение плотности пластинки, если в точке, удалённой от указанной вершины на , плотность равна 5. Отв.

12. Найти момент инерции однородного круга радиуса R относительно точки, лежащей на окружности. Отв. .

13. При какой замене переменных x и y на u и v параллелограмм, ограниченный прямыми x+y= 1, x+y= 2, 2x-y= 1, 2x-y= 3 на плоскости XOY перейдёт в прямоугольник на плоскости UOV со сторонами, параллельными координатным осям? Сделать чертёж.

14. Вычислить , сделав замену, подобранную в задаче 13 (область D – указанный в задаче параллелограмм). Отв. .

15. Подобрать замену переменных x и y на u и v, при которой область D на плоскости XOY, ограниченная линиями xy=1, xy=2, x-y=1, x-y+1=0, (x>0, y>0), перейдёт в прямоугольник на плоскости UOV, стороны которого параллельны координатным осям. Сделать чертёж.

16. С помощью тройного интеграла найти объём тела, ограниченного поверхностями . Отв.

17. Найти массу однородного тела, ограниченного поверхностями . Отв.

18. В трёхкратном интеграле поменять порядок интегрирования в последовательности: а) y,x,z; б) z,x,y.

19. При каком значении параметра a объём тела, ограниченного поверхностями равен заданному числу V? Отв. .

20. Вычислить 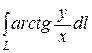, где L – часть спирали Архимеда ρ=2φ, заключённая внутри круга радиуса R с центром в полюсе. Отв.

21. Найти длину дуги пространственной кривой между точками (0,0,0) и (3,3,2). Отв. 5.

22. Вычислить , где L – замкнутый контур квадрата с вершинами (1,0), (0,1), (-1,0), (0,-1). Отв. 0.

23. Вычислить Отв. 0.

24. Доказать, что величина интеграла 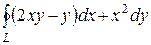, где L – замкнутый контур, выражает площадь области, ограниченной этим контуром.

25. Найти функцию U(x,y,z) по её полному дифференциалу
Отв. .

26. Сила по величине обратно пропорциональна расстоянию точки её приложения от оси OZ, перпендикулярна к этой оси и направлена к ней. Найти работу силы при движении точки массы m под действием этой силы по окружности x= cos t, y= 1, z = sin t от точки A (1,1,0) до точки B (0,1,1).

Отв. 0,5 k ln2, k – коэффициент пропорциональности.

Дата добавления: 2015-10-30