
Читайте также:
|
Задачи
Задания 1-15: Вычислить двойной интеграл по заданной области D:
1. а) 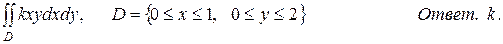
б) 
2. а) 
б) 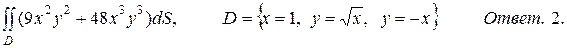
3. а) 
б) 
4. а) 
б) 
5. а) 
б) 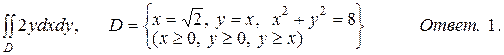
6. а) 
б) 
7. а) 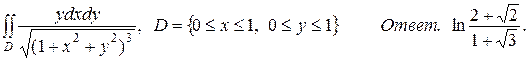
б) 
8. а) 
б) 
9. а) 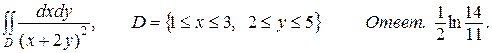
б) 
10. а) 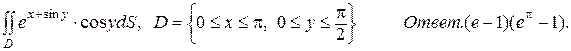
б) 
11.а) 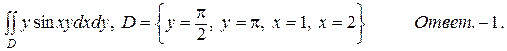
б) 
12. а) 
б) 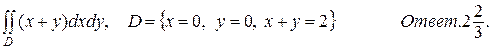
13. а) 
б) 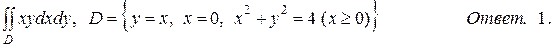
14. а) 
б) 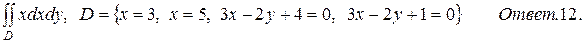
15. а) 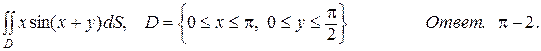
б) 
Задания 16-20: Записать  через повторный двумя способами и найти площадь области D:
через повторный двумя способами и найти площадь области D:
16. 
17. 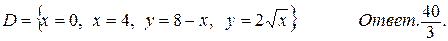
18. 
19. 
20. 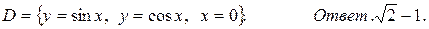
Задания 21-25: Изменить порядок интегрирования:
21. 
22. 
23. 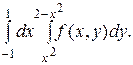
24. 
25. 
Задания 26-30: Построить область, площадь которой выражается заданным повторным интегралом. Изменить порядок интегрирования и найти площадь:
26. 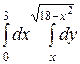 Ответ.
Ответ. 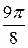
27.  . Ответ.
. Ответ. 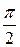
28. 
29. 
30. 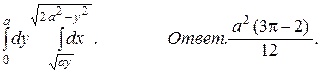
Задания 31-40: Вычислить двойной интеграл в полярных координатах:
31.  , D – круг
, D – круг 
32.  , D – часть кольца
, D – часть кольца  .
.

33. 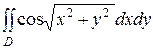 , D – определена неравенствами
, D – определена неравенствами  .
.

34. 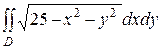 , D – часть круга радиуса 5 с центром в точке O(0, 0), лежащая в первой четверти. Ответ.
, D – часть круга радиуса 5 с центром в точке O(0, 0), лежащая в первой четверти. Ответ. 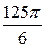
35.  , D – кольцо между окружностями
, D – кольцо между окружностями
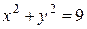 и
и  Ответ. 416 π.
Ответ. 416 π.
36.  ,
,  .
. 
37. 

38.. 

39. 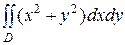 , D – круг
, D – круг  .
. 
40. 
Задания 41-45: С помощью двойного интеграла в полярных координатах найти площадь фигуры, ограниченной линией.
41.  Ответ.
Ответ. 
42.  Ответ.
Ответ. 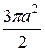
43. 
44. 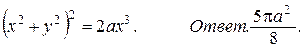
45. 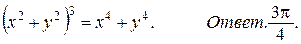
Задания 46-60: С помощью двойного интеграла найти объём тела, ограниченного указанными поверхностями (в задачах, помеченных звёздочкой, рекомендуется перейти к полярным координатам).
46. 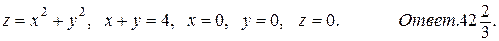
47. 
48.*  . Ответ. 24π
. Ответ. 24π
49. * 
 .
.
50. 
51. 
52. 
53. 
54. 
55. * 
56. * 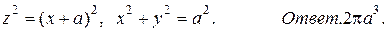
57. * 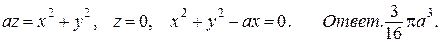
58. * 
59. * 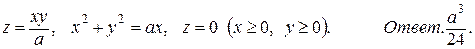
60. * 
Задание 61-75: Использовать физический смысл двойного интеграла (в задачах, помеченных звёздочкой, примените полярные координаты).
61. * Найти массу пластинки, занимающей область D, ограниченную линиями  и имеющую поверхностную плотность
и имеющую поверхностную плотность 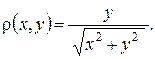 Ответ. 4.
Ответ. 4.
62. * Найти массу пластинки, занимающей область D, ограниченную линиями 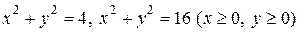 , если поверхностная плотность в каждой точке области равна
, если поверхностная плотность в каждой точке области равна 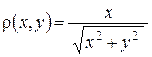 . Ответ. 6.
. Ответ. 6.
63. Найти центр масс однородной области, ограниченной линиями x– 3 y= 0, x+y= 8, x= 3. Ответ. 
64. Найти центр масс однородной области, ограниченной линиями 
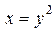 , если плотность масс постоянна и равна 1. Ответ.
, если плотность масс постоянна и равна 1. Ответ. 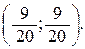
65.* Найти центр масс однородной фигуры, ограниченной линиями 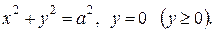 Ответ.
Ответ. 
66. Найти массу области D, ограниченной линиями 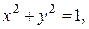
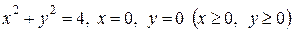 , если поверхностная плотность в каждой точке области равна
, если поверхностная плотность в каждой точке области равна  . Ответ. 2.
. Ответ. 2.
67.* Найти массу области D, ограниченной линиями 
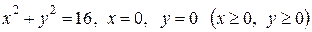 , имеющей поверхностную плотность
, имеющей поверхностную плотность 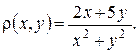 Ответ. 7.
Ответ. 7.
68.* Найти массу области D, ограниченной линиями 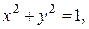
 , имеющей поверхностную плотность
, имеющей поверхностную плотность 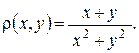 Ответ. 6.
Ответ. 6.
69. * Найти массу области D, ограниченной линиями 
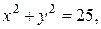
 , если поверхностная плотность
, если поверхностная плотность  . Ответ. 15.
. Ответ. 15.
70.* Найти массу плоской области D, ограниченной линиями 

 , если поверхностная плотность равна
, если поверхностная плотность равна
 Ответ. 10.
Ответ. 10.
71. Найти массу пластинки, имеющей форму прямоугольного треугольника с катетами OB=a и OA=b, если плотность её в любой точке равна расстоянию от точки до катета OA. Ответ. 
72. Найти моменты инерции однородного треугольника, ограниченного прямыми  , относительно осей координат.
, относительно осей координат.
Ответ. 

73. Найти момент инерции относительно оси OY однородной фигуры, ограниченной линиями  . Ответ.
. Ответ. 
74.* Найти массу круглой пластинки радиуса R, если плотность её пропорциональна квадрату расстояния от точки до центра и равна 1 на краю пластинки. Ответ. 
75. Найти момент инерции однородной фигуры, ограниченной линиями 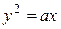 , y=a, x= 0, относительно прямой x = –a. Ответ.
, y=a, x= 0, относительно прямой x = –a. Ответ. 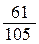
Задание 76-90: Вычислить криволинейный интеграл:
76. а)  L – дуга линии x = ln y между точками A (0, 1) и B (1, e).
L – дуга линии x = ln y между точками A (0, 1) и B (1, e).
Ответ. 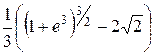 .
.
б) 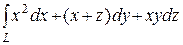 , L – дуга кривой
, L – дуга кривой 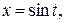

 Ответ. 1,9.
Ответ. 1,9.
77. а)  , L – дуга окружности x=R cos t, y=R sin t, лежащая в I четверти.
, L – дуга окружности x=R cos t, y=R sin t, лежащая в I четверти.
Ответ. 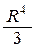 .
.
б)  , L – отрезок прямой от точки A (2,1,0) до точки B (4,3,1). Ответ.
, L – отрезок прямой от точки A (2,1,0) до точки B (4,3,1). Ответ. 
78. а)  , L – дуга кривой
, L – дуга кривой 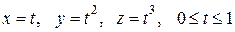
Ответ. 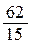
б) 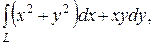 L – дуга кривой
L – дуга кривой  от точки A (0,1) до
от точки A (0,1) до
точки B (1, e). Ответ. 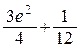
79.  а)
а)  , L – дуга тангенсоиды
, L – дуга тангенсоиды 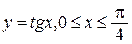
Ответ. 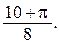
 б)
б)  , L – дуга кривой
, L – дуга кривой 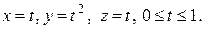
Ответ. 1.
 80. а)
80. а) 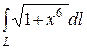 , L – дуга линии
, L – дуга линии 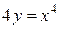 между точками O (0,0) и A (1,1/4).
между точками O (0,0) и A (1,1/4).
Ответ. 
б) 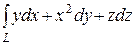 , L – дуга кривой
, L – дуга кривой 
Ответ. 

80. а)  , L – дуга линии
, L – дуга линии 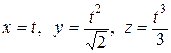 между точками O(0,0,0)
между точками O(0,0,0)
и  . Ответ.
. Ответ. 
б) 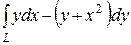 , L – дуга параболы
, L – дуга параболы  , расположенная над осью OX и пробегаемая против хода часовой стрелки. Ответ. –4
, расположенная над осью OX и пробегаемая против хода часовой стрелки. Ответ. –4
82. а)  L – контур треугольника с вершинами A (1,0), B (01), O (0,0).
L – контур треугольника с вершинами A (1,0), B (01), O (0,0).
Ответ. 
б) 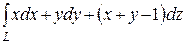 , L – отрезок прямой от точки A (1,1,1) до точки
, L – отрезок прямой от точки A (1,1,1) до точки
B (2,3,4). Ответ. 13.
83.* а)  , L – окружность
, L – окружность 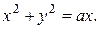 Ответ.
Ответ. 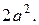
б)  , L – дуга винтовой линии
, L – дуга винтовой линии 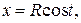

 от точки ее пересечения с плоскостью
от точки ее пересечения с плоскостью  до точки пересечения с плоскостью
до точки пересечения с плоскостью 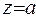 . Ответ. 0
. Ответ. 0


 84. а)
84. а)  , где AB – дуга полукубической параболы между точками
, где AB – дуга полукубической параболы между точками
 и
и  . Ответ.
. Ответ. 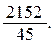
б)  , OA – четверть окружности
, OA – четверть окружности 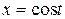 ,
, 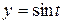 ,
, 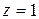 , пробегаемая в направлении возрастания параметра t. Ответ.
, пробегаемая в направлении возрастания параметра t. Ответ. 
85. а) 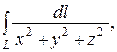 L – первый виток винтовой линии
L – первый виток винтовой линии  ,
, 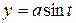 ,
,  . Ответ.
. Ответ. 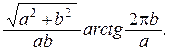
б) 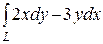 , L – контур треугольника с вершинами A (1,2), B (3,1), C (2,5). Ответ. 17,5.
, L – контур треугольника с вершинами A (1,2), B (3,1), C (2,5). Ответ. 17,5.
86. а)  , L – дуга линии
, L – дуга линии  . Ответ.
. Ответ. 
б) 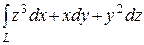 , L – дуга линии
, L – дуга линии  .
.
Ответ. 
87. а) 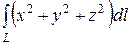 , L – отрезок прямой между точками A (1,1,1)и B (3,0,3) Ответ. 27.
, L – отрезок прямой между точками A (1,1,1)и B (3,0,3) Ответ. 27.
б) 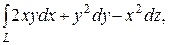 L – дуга линии пересечения гиперболоида
L – дуга линии пересечения гиперболоида  с плоскостью y=x от точки (1,1,0)до точки
с плоскостью y=x от точки (1,1,0)до точки  .
.
Ответ. 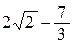
88. а) 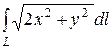 , L – окружность
, L – окружность  .
.
Ответ. 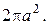
б) 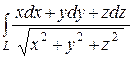 , L – отрезок прямой между точками A (0,1,1)
, L – отрезок прямой между точками A (0,1,1)
и B (1,0,2).  Ответ.
Ответ. 
89.  а)
а) 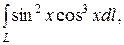 L – дуга линии
L – дуга линии 

Ответ. 
б) 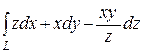 , L – дуга кривой
, L – дуга кривой  .
.
Ответ.  .
.
90. а)  , L – дуга кривой
, L – дуга кривой 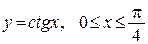 .
.
Ответ. 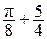
б)  , L – дуга линии
, L – дуга линии 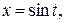


 . Ответ. 1,9.
. Ответ. 1,9.
Задания 91-120: Использовать физический смысл криволинейных интегралов
91. Найти координаты центра масс дуги кривой  ,
,  ,
,  ,
, 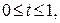 если в каждой точке
если в каждой точке  линейная плотность равна
линейная плотность равна 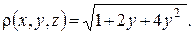 Ответ.
Ответ. 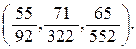
92. Найти массу материальной дуги кривой  с линейной плотностью
с линейной плотностью  Ответ. 24.
Ответ. 24.


 93. Найти массу материальной дуги кривой
93. Найти массу материальной дуги кривой  , если линейная плотность равна
, если линейная плотность равна  Ответ.
Ответ. 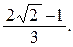
94.  Найти массу первой арки циклоиды
Найти массу первой арки циклоиды  , если плотность массы в каждой точке кривой равна квадрату ординаты.
, если плотность массы в каждой точке кривой равна квадрату ординаты.
Ответ. 
95. Найти массу дуги линии 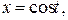

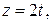
 с линейной плотностью ρ(x,y,z) = xyz. Ответ.
с линейной плотностью ρ(x,y,z) = xyz. Ответ. 
96. Найти массу четверти окружности  , расположенной в первом квадранте, если плотность её в каждой точке пропорциональна кубу ординаты этой точки (коэффициент пропорциональности равен β).
, расположенной в первом квадранте, если плотность её в каждой точке пропорциональна кубу ординаты этой точки (коэффициент пропорциональности равен β).
Ответ. 
97. Найти массу материальной дуги линии  , если
, если  линейная плотность в каждой точке равна
линейная плотность в каждой точке равна 
Ответ. 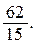
98. Найти массу первого витка винтовой линии 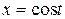 ,
, 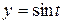 ,
,  , если плотность в каждой точке линии равна модулю радиус-вектора этой точки.
, если плотность в каждой точке линии равна модулю радиус-вектора этой точки.
Ответ. 
 99. Найти массу четверти эллипса
99. Найти массу четверти эллипса  , лежащей в первом квадранте, если плотность в каждой точке равна произведению координат этой точки.
, лежащей в первом квадранте, если плотность в каждой точке равна произведению координат этой точки.
Ответ. 
100. Найти массу четверти окружности  , расположенной в первом квадранте, если плотность массы в каждой точке пропорциональна абсциссе этой точки (коэффициент пропорциональности a). Ответ.
, расположенной в первом квадранте, если плотность массы в каждой точке пропорциональна абсциссе этой точки (коэффициент пропорциональности a). Ответ. 
101. Найти массу материальной дуги линии 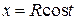 ,
, 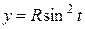 ,
, 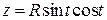 ,
,  , если линейная плотность её равна
, если линейная плотность её равна  Ответ.
Ответ. 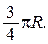
102. Найти массу участка цепной линии  между точками x 1=0 и x 2 =a, если плотность в каждой её точке обратно пропорциональна ординате точки и равна δ в точке (0, a). Ответ. δa.
между точками x 1=0 и x 2 =a, если плотность в каждой её точке обратно пропорциональна ординате точки и равна δ в точке (0, a). Ответ. δa.
103. Найти массу дуги конической винтовой линии 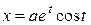 ,
, 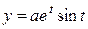 ,
,  от точки O (0,0,0) до A (a,0, a), если плотность в каждой точке кривой выражается формулой
от точки O (0,0,0) до A (a,0, a), если плотность в каждой точке кривой выражается формулой  Ответ.
Ответ. 
104. Найти координаты центра масс дуги винтовой линии 

 , если линейная плотность в каждой точке пропорциональна произведению координат этой точки.
, если линейная плотность в каждой точке пропорциональна произведению координат этой точки.
Ответ. 
105. Найти массу лемнискаты 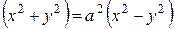 , если линейная плотность в каждой её точке равна модулю ординаты точки. Ответ.
, если линейная плотность в каждой её точке равна модулю ординаты точки. Ответ. 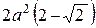
106. Найти работу силы  при перемещении точки вдоль дуги синусоиды
при перемещении точки вдоль дуги синусоиды  . Ответ.
. Ответ. 
107. Найти работу, производимую силой  при перемещении точки вдоль дуги астроиды
при перемещении точки вдоль дуги астроиды 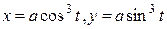 от точки A (a, 0) до точки
от точки A (a, 0) до точки  Ответ.
Ответ. 
108. Найти работу поля  при передвижении точки вдоль дуги линии
при передвижении точки вдоль дуги линии  Ответ. 1,1.
Ответ. 1,1.
109. Найти работу силы 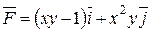 при перемещении материальной точки вдоль дуги эллипса x= cos t, y= 2sin t, расположенной в первой четверти. Ответ.
при перемещении материальной точки вдоль дуги эллипса x= cos t, y= 2sin t, расположенной в первой четверти. Ответ. 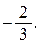
110. Найти работу, производимую силой  при перемещении точки вдоль ломанной ABC, A (1,1), B (3,1), C (3,5).
при перемещении точки вдоль ломанной ABC, A (1,1), B (3,1), C (3,5).
Ответ. 190.
111. Показать, что работа, производимая силой  , не зависит от вида пути с началом в точке O (0,0) и концом в точке A (1,1). Найти эту работу. Ответ. 1.
, не зависит от вида пути с началом в точке O (0,0) и концом в точке A (1,1). Найти эту работу. Ответ. 1.
112. Показать, что работа, производимая силой 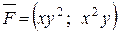 , не зависит от пути перемещения точки, и найти эту работу, если точка перемещается из положения O (0,0) в положение A (2,2). Ответ. 8.
, не зависит от пути перемещения точки, и найти эту работу, если точка перемещается из положения O (0,0) в положение A (2,2). Ответ. 8.
113. Показать, что работа поля  не зависит от вида пути перемещения точки. Найти работу при перемещении точки из положения (0,0) в положение (1,1). Ответ. 2.
не зависит от вида пути перемещения точки. Найти работу при перемещении точки из положения (0,0) в положение (1,1). Ответ. 2.
114. Показать, что работа силы  не зависит от формы пути, а зависит только от начальной и конечной точек перемещения. Найти работу этой силы при перемещении точки из положения O (0,0) в положение M (1,1). Ответ. 1.
не зависит от формы пути, а зависит только от начальной и конечной точек перемещения. Найти работу этой силы при перемещении точки из положения O (0,0) в положение M (1,1). Ответ. 1.
115. Показать, что работа при перемещении точки в поле  не зависит от формы пути. Найти работу при перемещении точки из положения (0,0)в положение (π, π). Ответ.
не зависит от формы пути. Найти работу при перемещении точки из положения (0,0)в положение (π, π). Ответ.  .
.
116. Проекции силы `F на оси координат задаются формулами 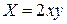 и
и  . Показать, что работа силы при перемещении точки зависит только от начального и конечного положений точки и не зависит от формы пути. Найти работу при перемещении точки из положения (1,0) в положение (0,3). Ответ. 0.
. Показать, что работа силы при перемещении точки зависит только от начального и конечного положений точки и не зависит от формы пути. Найти работу при перемещении точки из положения (1,0) в положение (0,3). Ответ. 0.
117. Поле образованно силой  . Определить работу этого поля при перемещении массы m по контуру, образованному полуосями координат и первой четвертью эллипса
. Определить работу этого поля при перемещении массы m по контуру, образованному полуосями координат и первой четвертью эллипса  ,
, 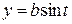 . Ответ.
. Ответ. 
118. В каждой точке M эллипса  ,
, 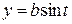 приложена сила `F, равная по величине расстоянию от точки M до центра эллипса и направленная к центру эллипса. Найти работу силы `F при перемещении точки вдоль дуги эллипса, лежащей в первом координатном угле. Ответ.
приложена сила `F, равная по величине расстоянию от точки M до центра эллипса и направленная к центру эллипса. Найти работу силы `F при перемещении точки вдоль дуги эллипса, лежащей в первом координатном угле. Ответ. 
119. В каждой точке плоскости на материальную точку действует сила `F. Найти работу силы `F при перемещении точки из начала координат в точку (1,1) по двухзвенной ломаной, звенья которой параллельны осям координат (рассмотреть два случая). Ответ. 1,5 и 1.
120. В каждой точке плоскости на материальную точку действует сила, имеющая постоянную величину F и направление положительной оси абсцисс. Найти работу этой силы при перемещении точки вдоль дуги окружности  лежащей в I квадранте. Ответ. FR.
лежащей в I квадранте. Ответ. FR.
Задания 121-130: Доказать, что заданное выражение является дифференциалом некоторой функции; найти эту функцию:
121. 
122. 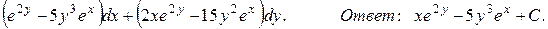
123. 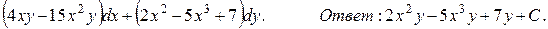
124. 
125. 
126. 
127. 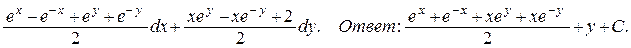
128. 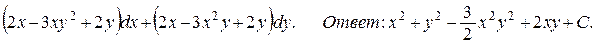
129. 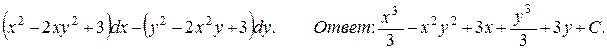
130. 
Задания 131-135: Найти функцию U (x, y), полным дифференциалом которой является данное подынтегральное выражение и вычислить интеграл, используя формулу Ньютона-Лейбница для криволинейного интеграла.
131. 
132. 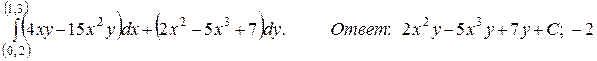
133. 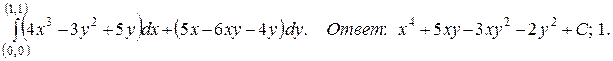
134. 
135. 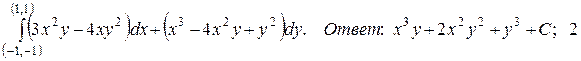
Дата добавления: 2015-10-30; просмотров: 795 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Розглянемо неоднорідне рівняння Фредгольма 2-го роду | | | Дополнительные задачи |