Розглянемо неоднорідне рівняння Фредгольма 2-го роду

, (3.1)

в якому є дійсною, неперервною на функцією, ядро , а – задане число. Можливі два випадки:

1) , де – власне значення ядра , а – відповідна йому власна функція. В цьому випадку розв’язком рівняння (3.1) буде

, (3.2)

де , а функція називається резольвентою ядра ;

2) , тобто параметр в рівнянні (3.1) дорівнює деякому власному значенню ядра . Нехай – власні функції ядра, що відповідають власним значенням .

а) якщо функція ортогональна всім власним функціям (), тобто , то розв’язок рівняння (3.1) існує, але не єдиний:

, (3.3)

де – деякі довільні сталі.

б) якщо функція неортогональна хоча б одній з власних функцій , то розв’язку рівняння (3.1) не існує.

Приклад. Дослідимо розв’язок рівняння

(3.4)

при різних значеннях параметрів . Відповідне однорідне рівняння має вигляд

. (3.5)

Ядро рівняння (3.5) вироджене і симетричне. Тому його розв’язок шукаємо у формі , який підставляємо в (3.5):

.

Прирівнюючи коефіцієнти при нульовій та першій степенях х справа й зліва в цьому співвідношенні, маємо

Звідси , і .

1) Нехай , тоді розв’язок неоднорідного рівняння (3.4) можемо шукати у вигляді , після підстановки якого в (3.4) отримуємо

.

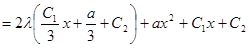Прирівнюючи коефіцієнти при нульовій та першій степенях х справа й зліва в цьому співвідношенні і розв’язуючи отримані рівняння відносно , маємо , . Отже, розв’язок рівняння (3.4) має вигляд .

2) . Розв’язок рівняння (3.4) існує тільки при умові

.

В цьому випадку розв’язком буде вираз

.

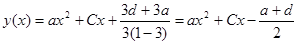3) . Розв’язок рівняння (3.4) існує тільки при умові

.

Тут розв’язком буде вираз

.

НЕоднорідне рівняння Фредгольма 1-го роду

. (4.1)

Рівняння Фредгольма 1-го роду належать до некоректно поставлених задач, а його розв’язки є нестійкими відносно збурень функції , тобто невелика зміна функції призводить до значних змін в розв’язку . Це означає, що при розв’язуванні фізичних задач невелика похибка у вихідних даних може настільки змінити розв’язок, що він може не мати нічого спільного з тим фізичним процесом, який описує дане рівняння, і навіть може призвести до того, що розв’язок просто не буде існувати.

Однак А.Н. Тіхонов запропонував регуляризуючий алгоритм, який дозволяє знайти функцію як завгодно близьку до точного розв’язку рівняння. Отже, рівняння Фредгольма 1-го роду можна розв’язати тільки наближено.

Дата добавления: 2015-10-30