
Читайте также:
|
Основні поняття та класифікація інтегральних рівнянь
Інтегральним рівнянням називається рівняння, яке містить невідому функцію під знаком інтеграла.
Наприклад
 , (
, ( ) (1.1)
) (1.1)
або
 . (1.2)
. (1.2)
Тут 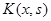 і
і  – задані функції, а
– задані функції, а  – шуканий розв’язок. Функція
– шуканий розв’язок. Функція 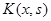 називається ядром інтегрального рівняння,
називається ядром інтегрального рівняння,  – параметр.
– параметр.
Класифікація інтегральних рівнянь
В даному курсі вивчаються тільки лінійні інтегральні рівняння, коли шукана функція  входить у рівняння лінійно. Вони класифікуються наступним чином:
входить у рівняння лінійно. Вони класифікуються наступним чином:
1. а) якщо шукана функція міститься тільки під знаком інтеграла, то рівняння називається інтегральним рівнянням першого роду. Такими рівняннями є рівняння вигляду
 (1.3)
(1.3)
або
 ; (1.4)
; (1.4)
б) якщо шукана функція міститься також і поза знаком інтеграла (див., наприклад, (1.1) і (1.2)), то рівняння називається інтегральним рівнянням другого роду.
2. а) якщо межі інтегрування фіксовані, то інтегральне рівняння називається рівнянням Фредгольма (випадки (1.1) і (1.3));
б) якщо ж межі інтегрування змінні (випадки (1.2) і (1.4)), то інтегральне рівняння називається рівнянням Вольтерра.
3. Рівняння (1.1)-(1.4) називаються однорідними, якщо  і неоднорідними при
і неоднорідними при  .
.
Зведення диференціальних рівнянь до інтегральних
Інтегральні рівняння можна отримати з диференціальних.
1. Нехай задано задачу Коші для диференціального рівняння 1-го порядку:
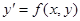 . (1.5а)
. (1.5а)
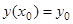 (1.5б)
(1.5б)
Звідси  або
або
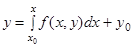 . (1.6)
. (1.6)
Це нелінійне інтегральне рівняння.
2. Нехай задано задачу Коші для лінійного неоднорідного диференціального рівняння n -го порядку:
 , (1.7а)
, (1.7а)
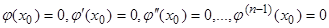 . (1.7б)
. (1.7б)
Покладемо
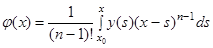 , (1.8)
, (1.8)
де  – нова невідома функція. Диференціюючи цей вираз n раз, маємо
– нова невідома функція. Диференціюючи цей вираз n раз, маємо
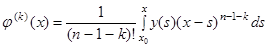 (
(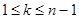 ),
),
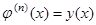 .
.
Підставляючи останні вирази для  в ліву частину рівняння (1.7a), отримаємо
в ліву частину рівняння (1.7a), отримаємо
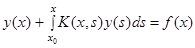 , (1.9)
, (1.9)
де 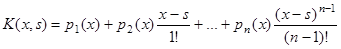 . Таким чином, задача (1.7) звелася до розв’язування інтегрального рівняння Вольтерра 2-го роду (1.9). Визначивши з (1.9) функцію
. Таким чином, задача (1.7) звелася до розв’язування інтегрального рівняння Вольтерра 2-го роду (1.9). Визначивши з (1.9) функцію  , знаходимо
, знаходимо 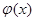 згідно (1.8).
згідно (1.8).
Фізичні задачі, які приводять до інтегральних рівнянь
1. До рівняння Вольтерра 1-го роду приводить задача визначення потенціальної енергії поля в якому частинка здійснює коливальний рух за відомою залежністю періоду коливань частинки від її енергії. Нехай 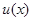 – потенціальна енергія, яка вважається парною, монотонно зростаючою при
– потенціальна енергія, яка вважається парною, монотонно зростаючою при 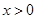 функцією, Е – енергія частинки, а m – її маса. Тоді за законом збереження енергії
функцією, Е – енергія частинки, а m – її маса. Тоді за законом збереження енергії 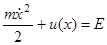
 . Інтегруємо це рівняння, відокремлюючи змінні:
. Інтегруємо це рівняння, відокремлюючи змінні:  . Звідси
. Звідси 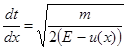 ,
, 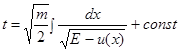 . Нехай
. Нехай 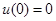 , тоді період коливань буде
, тоді період коливань буде 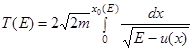 , де
, де  корінь рівняння
корінь рівняння 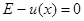 .
.
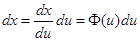 ,
,  . Тоді
. Тоді
 . (1.10)
. (1.10)
Нехай функція 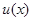 невідома, але відома залежність
невідома, але відома залежність 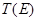 для деякого інтервалу енергій Е. Тоді задача знаходження функції
для деякого інтервалу енергій Е. Тоді задача знаходження функції 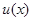 зводиться до розв’язування інтегрального рівняння Вольтерра 1-го роду (1.10) відносно функції
зводиться до розв’язування інтегрального рівняння Вольтерра 1-го роду (1.10) відносно функції 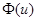 . Визначивши
. Визначивши 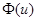 , знаходимо залежність
, знаходимо залежність 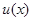 з рівняння
з рівняння  ,
, 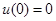 .
.
2. Рівняння Вольтерра 2-го роду типові при описанні фізичних процесів, пов’язаних з явищами після дії, наприклад, коливальний контур.
3. Рівняння Фредгольма 1-го роду є типовими при математичній обробці даних експерименту в задачі відновлення розмитого зображення.
4. До рівнянь Фредгольма 2-го роду приволять задачі про коливання струни під дією зовнішньої сили.
Дата добавления: 2015-10-30; просмотров: 84 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Інтегральна або комплексна оцінка соціально-економічних явищ. | | | Розглянемо неоднорідне рівняння Фредгольма 2-го роду |