Задачі, що зводяться до транспортної

Виробничо-транспортна задача

Нехай у пунктах А_і можуть бути побудовані підприємства, що виробляють продукцію обсягом а_і. Ця продукція призначена для пунктів споживання В_j з попитом b_j. Значення матриці витрат на транспортування представлені в сумі разом із значеннями матриці витрат на виробництво продукції в пункті А_і. Потрібно вибрати місце розміщення нових підприємств, обсяги виробництва і план перевезень таким чином, щоб сумарні витрати були найменшими.

Задача про призначення або розподіл робіт між різними виконавцями

Нехай є n літаків різних типів, які потрібно розподілити між n авіалініями. c_ij – кількість пасажирів, що перевезе і -тий літак, якщо він буде призначений на j -ту авіалінію. Потрібно так розподілити літаки на авіалінії, щоб кількість перевезених пасажирів була максимальною.

Нехай є n робіт (механізмів, верстатів, установок) яких треба розподілити між n робітниками (інженерами, бригадами). При цьому кожен виконавець може виконувати будь-яку роботу, але з різною продуктивністю праці і кожен виконавець може бути призначений тільки для виконання однієї роботи. Потрібно таким чином розподілити роботи між виконавцями, щоб продуктивність праці була найбільшою. Замість продуктивності праці можна застосувати інші критерії – час виконання, вартість робіт, заробітна плата.

Особливість математичної постановки таких задач полягає в тому, що необхідно сформувати квадратну матрицю

Х =êê х_ij êê, де

0, у протилежному випадку.

х_ij =

Математична постановка такої задачі запишеться таким чином:

1) цільова функція має вигляд

, (2.1.8)

де c_ij – один з критеріїв (продуктивність праці, час виконання роботи, зарплата);

2) при обмеженнях

x _ij ³ 0. (2.1.9)

Нижче подається приклад розв”язання типової задачі про призначення, виконаний у Mathcad 2000 Pro. У випадку, коли формула настільки довга, що не поміщається на робочому листку, перенос її частини виконується тільки після знаку “+” за допомогою комбінації клавіш Ctrl + Enter.

Приклад. На п”яти типах токарних верстатів можуть працювати п”ять токарів, причому кожен токар може працювати на будь-якому типі верстата, але з різною продуктивністю праці і кожен токар може бути призначений тільки за один верстат. Матриця оцінок продуктивностей праці для всіх призначень наведена у табл.2.1.2.

Таблиця 2.1.2 – Матриця оцінок продуктивностей праці для призначень робітників

(в умовних одиницях)

Виконавці	Види робіт та матриця продуктивностей праці

Інтерпретація результатів розрахунків: перший робітник має бути призначений за четвертий тип верстата; другий – за другий тип; третій – за третій; четвертий – за п”ятий; п”ятий – за перший.

Задача про взаємозамінне обладнання

Продукція і -ого виду може вироблятися на будь-якому j -му обладнанні із витратами машинного часу l_ij. Відомі наявний фонд робочого часу кожного виду обладнання А_j та план випуску кожного виду продукції В_і. Необхідно знайти таку кількість продукції кожного і -ого виду, що виробляється на j -му обладнанні х_ij, щоб вибраний критерій ефективності (витрати, прибуток і т.п.) був максимальним чи відповідно мінімальним.

Математична модель має такий вигляд:

- цільова функція (2.1.10)

- обмеження по балансу між потрібним і наявним фондом робочого часу обладнання , (2.1.11)

дотриманню плану випуску продукції , (2.1.12)

додатності значень х_ij ³ 0. (2.1.13)

Дана постановка задачі відрізняється від транспортної тільки наявністю величини l_ij, яка щодо транспортної постановки буде інтерпретуватися, як кількість вантажу, що його може перевезти одиниця і -го транспорту на j -му маршруті. Для зведення цієї задачі до транспортної потрібно виключити l_ij, що роблять, виразивши всі величини через деяке стандартизоване l_ijст. Стандартизованим вважається вид транспорту з найменшою продуктивністю. Позначивши , отримаємо , , , 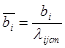а підставивши у попередню модель, отримаємо модель відкритої транспортної задачі

,max (2.1.14)

, (2.1.15)

, (2.1.16)

. (2.1.17)

Розподіл обладнання між ремонтними структурами

Бурові та нафтогазовидобувні підприємства виконують деякі види ремонтів обладнання на спеціалізованих базах виробничого обслуговування (БВО). Інженерна служба при цьому має вирішити, скільки і якої техніки слід ремонтувати на тих чи інших БВО. Собівартість ремонту при цьому визначатиметься сумою собівартостей власне ремонту та транспортних витрат. Математична постановка такої задачі матиме вигляд за формулами (2.1.4 - 2.1.7) при позначеннях: х_ij – кількість обладнання і -го виду, що ремонтується на j -ій базі; а_і – сумарна потреба в ремонті і -го обладнання; b_j – потужність j -ої бази виробничого обслуговування;

с_ij – вартість ремонту, доставки та монтажу-демонтажу техніки.

5 Обмеження пропускної здатності

Приклад. За умовою задачі, поданої в таблиці, на ділянці дороги від А₂ до В₁ можна перевезти лише 15 одиниць продукції із 45.

Вj Аі	В1	В2	В3
А1 55
А2 45
А3 50

Для розв”язання задачі споживача В₁ “розділяють” на фіктивного з потребою в заблоковані 20 одиниць вантажу та нульовою собівартістю перевезень від другого постачальника, та дійсного із дозволеними для перевезення 15-ма одиницями вантажу. Умова задачі матиме такий табличний вигляд:

Вj Аі	В1	В1^*	В2	В3
А1 55
А2 45
А3 50

Якщо від одного або декількох постачальників необхідно перевезти вантаж у заданій кількості, незважаючи на собівартість перевезень (так звані обов”язкові поставки), то в умові задачі зменшуємо потужність відповідних постачальників та попит відповідних споживачів на величину обов”язкової поставки, а дальше розв”язуємо задачу звичайними алгоритмами.

Задача планування оптимального випуску продукції

Математична постановка такої задачі відрізняється від попередньої видом цільової функції та обмежень. Задача може бути розв”язана більш загальним, ніж транспортний, алгоритмом, який отримав назву симплекс-метод. Розглянемо один із типових прикладів.

На підприємстві випускається продукція (деталі) видів B_j (j=1,2,…n), кожен з яких обробляється на верстатах A_i (i = 1,2,…m) (послідовність обробки не має значення). На обробку однієї деталі виду В_j,на верстаті А_i витрачається час а_ij (годин). Для кожного із верстатів А_i, фонд робочого часу (максимально можливий час роботи одного верстата) становить b_j годин. Прибуток від продажу одиниці деталі виду В_j становить с _j. Дані задачі в загальному вигляді занесені в табл. 2.1.3.

Таблиця 2.1.3 — Задача лінійного програмування у табличному вигляді

Верстати	Види деталей	Фонд часу
В1	В2	···	Вп
А1	а11	а12	...	а1n	b1
А2	а21	а22	...	a2n	b2
···	…	…	…	…	…
Аm	am1	am2	...	аmn	bm
Прибуток	с1	с2	...	сп

Потрібно скласти такий план випуску продукції видів Bj, щоб прибуток від реалізації всієї продукції виявився максимальним.

Якщо позначити через x_j (j=1,2,...,n) відповідно кількість одиниць продукції (деталей) виду Bj призначених до випуску, то вищенаведену задачу можна записати у вигляді системи нерівностей

a₁₁x₁ + a₁₂x₂ + …+ a_1nx_n £ b₁

a₂₁x₁ + a₂₂x₂ + …+ a_2nx_n £ b₂ (2.1.18)

…………………………………

a_m1x₁ + a_m2x₂ + …+ a_mnx_n £ b_m,

яка буде відображати суть обмежень при використанні ресурсів.

Прибуток від реалізації продукції, тобто цільова функція, буде мати вигляд

F = с₁x₁ + с₂x₂ + …+ с_nx_n. (2.1.19)

Продемонструємо реалізацію симплекс-методу розв”язання даної задачі із значеннями змінних, наведених у табл. 2.1.4.

Таблиця 2.1.4 – Таблиця вхідних даних

Верстати	Види деталей та витрати часу на одну деталь	Фонд часу bj, год
В1	В2	В3	В4
А1
А2
Аm
Прибуток сj, грн./од.

Необхідно максимізувати загальний прибуток, тобто цільову функцію

F = 13x₁+14x₂+15x₃+16x₄ ®max при обмеженнях:

6х₁+3х₂+7х₃+5х₄£ 4000

3х₁+4х₂+2х₃+6х₄£1500

4х₁+1х₂+5х₃+2х₄£ 4000

х₁, х₂, х₃, х₄ ³ 0.

Спочатку необхідно звести систему нерівностей до системи рівнянь. Роблять це, доповнюючи нерівності додатковими змінними х_n+j, де n – кількість нерівностей. У нашому прикладі n =3, j =1,2,3,4, отже отримаємо

6х₁+3х₂+7х₃+5х₄+х₅ =4000

3х₁+4х₂+2х₃+6х₄ +х₆ =1500

4х₁+1х₂+5х₃+2х₄ +х₇ =4000.

Економічний зміст додаткових змінних в обмеженнях визначається, як невикористаний обсяг ресурсу. Очевидно, якщо фонд часу буде використано повністю, то значення додаткових змінних будуть рівні нулю.

У цільову функцію ці змінні входять з нульовими коефіцієнтами. Якщо позначити остаточний результат цільової функції через F_опт, то можна записати

F_опт – 13х₁ – 14х₂ – 15х₃ – 16х₄ = 0.

Симплекс метод – це чисельний метод, який складається з декількох ітерацій розв”язування. На першому етапі (першій ітерації) приймають, що F_опт =0 (початкове наближення функції), тому

13х₁ – 14х₂ – 15х₃ – 16х₄ = 0,

що можливе за умови, коли всі змінні рівні нулю, а отже х₅ = 4000, х₆ = 1500, х₇ = 4000.

Останній запис має свій економічний зміст, а саме – на початковому етапі весь наявний ресурс (фонд робочого часу) є невикористаним.

На підставі попередніх викладок створюють так звану сиплекс-таблицю, зручну для застосування симплекс-алгоритму, суть якого полягає в тому, що розраховують так звані базисні змінні, переставляючи місцями за спеціальними правилами додаткові змінні, які на першому кроці є базисними, з основними (або вільними) змінними.

Базисні змінні	Фонд часу(ре-сурси bi)	Матриця аij для вільних змінних	bj/ais
х1	х2	х3	х4
-		-13	-14	-15	-16	-
х5
х6
х7

Оптимізація відбувається доти, поки коефіцієнти при вільних змінних в рядку цільової функції не стануть додатними. Це означатиме, що функція F досягла свого оптимального значення.

Симплекс-метод розв”язування задачі реалізовано у такому алгоритмі.

Визначаємо розв”язний стовпець та розв”язний рядок, які будуть визначати відповідно вільну та базисну змінні, що мінятимуться місцями. Розв”язний стовпець визначається через максимальне за модулем значення коефіцієнта в рядку цільової функції - max(êс₁ê, êс₂ê, êс₃ê, êс₄ê). Для нашого прикладу розв”язний стовпець відповідає вільній змінні х₄. Всі коефіцієнти цього стовпця позначимо а_{is .}

Розв”язний рядок визначається через мінімальне значення співвідношення кожного ресурсу b_i та коефіцієнта а_is в розв”язному стовпці

b_i/а_is ® min.

Для нашого прикладу цей рядок відповідатиме базисній змінні х₆.

На перехресті розв”язного рядка і розв”язного стовпця визначається розв”язний елемент a_rs.

Для нашого прикладу a_rs = 6. В подальшому індекси r та s будуть стосуватись до всіх величин відповідно розв”язних рядка та стовпця.

При взаємозаміні базисної та вільної змінних на наступних ітераціях всі члени матриці коефіцієнтів перераховуються за такими правилами:

для розв”язного рядка ;

для розв”язного стовпця ;

для розв”язного елемента ;

для решти елементів матриці 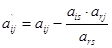в тому числі для ,

де всі позначення із штрихом стосуються елементів наступної ітерації у перерахунку симплекс-таблиці.

Так, для першої ітерації маємо

Базисні змінні	Вільні члени bі	Матриця aij для вільних змінних xj
х1	х2	х3	х6
-	24000/6	-30/6	-20/6	-58/6	16/6	-
х3	16500/6	21/6	-2/6	32/6	-5/6	51,56
х4	1500/6	3/6	4/6	2/6	1/6
х7	21000/6	18/6	-2/6	26/6	-2/6	80,77

А остаточний результат розв”язку буде виглядати таким чином

Базисні змінні	Вільні члени bі	Матриця aij для вільних змінних xj
х1	х4	х5	х6
-		2,95	5,73	1,46	2,41	-
х3		0,68	0,09	0,18	-0,14	-
х2		0,41	1,68	-0,09	0,32	-
х7		0,18	0,09	-0,82	0,36	-

Інтерпретація отриманих результатів

Результати розрахунку: х₁ =0 – випускати деталі першого виду не потрібно;

х₂ =113 – кількість деталей 2-го виду;

х₃ =523 – кількість деталей третього виду;

х₄ =0 – випускати деталі четвертого виду не потрібно.

Невикористаний час роботи (недовантаження) третього верстата становить

х₇ =1272 год;

у випадку обмежень виду ≥ тлумачити цю змінну необхідно, як кількість продукції, що може бути вироблена понад план.

Прибуток підприємства при умові реалізації всіх деталей становитиме

F=9432 грн.

Для небазисних вільних змінних у рядку цільової функції (х₁ =2,95 та х₄ =5,73)

отримані результати визначають відхилення цієї функції, коли значення даної змінної змінюється на одиницю.

Коефіцієнти при додаткових змінних у цільовій функції (х₅ =1,68 та х₆ =2,41) визначають ціну ресурсу, наприклад, ціну оренди верстатів або часу їх роботи.

Інші коефіцієнти визначають кількісні співвідношення між базисними й небазисними змінними в оптимальному плані.

Значення ціни ресурсу можна отримати, розв”язавши також двоїсту задачу до вищеподаної прямої задачі лінійного програмування. Поняття двоїстості визначає, наскільки модель чутлива до змін вхідних параметрів, тобто, якщо змінити ціну ресурсу, то чи залишиться даний план і надалі оптимальним.

Різницю у постановці прямої і двоїстої задач видно із розв”язку у програмному забезпеченні Mathcad 2001 Pro.

Розв”язок задачі можна отримати також у програмному забезпеченні Excel, що зводиться до таких кроків.

Заповнити таблицю вхідних даних

В клітинку А8 заносимо значення цільової функції: =СУММПРОИЗВ(Н2:Н5;В2:В5).

Перший масив складається із значень прибутку від реалізації кожної деталі, другий – із значень змінних х_і. У клітки С8:Е8 вводимо ліві частини нерівностей системи. У клітку С8 вводимо формулу =СУММПРОИЗВ(С2:С5; $B2:$B5), а у клітки D8 і Е8 – відповідно =СУММПРОИЗВ(D2:D5; $B2:$B5); =СУММПРОИЗВ(E2:E5; $B2:$B5).

У режимі відображення формул вхідні дані будуть виглядати таким чином

В меню Сервис вибираємо Поиск решения, де заповнюємо

Запускаємо команду на рахунок за допомогою Выполнить, після чого на екрані з”являється вікно Результаты поиска решения, у якому зберігаємо результати розрахунків.

Запитання та завдання

Сформулюйте умову транспортної задачі. Назвіть всі вхідні дані для розв”язку задачі, що задана табличним виглядом.

Сформулюйте математичну постановку транспортної задачі. Економічна суть цільової функції та обмежень.

Загальний алгоритм розв”язання транспортної задачі методом потенціалів.

Загальна схема розв”язання транспортної задачі в програмному забезпеченні Mathcad.

Загальна схема розв”язання транспортної задачі в програмному забезпеченні Excel.

Сформулюйте приклади економічних задач, які розв”язуються транспортними методами.

Яким чином розв”язується транспортна задача у випадку обмеження пропускної здатності?

Яким чином розв”язується транспортна задача у випадку обов”язкових поставок?

Сформулюйте задачу завантаження виробничої потужності. Поясніть відмінність цієї задачі порівняно із транспортною. Назвіть всі вхідні дані для розв”язання задачі, що задана табличним виглядом.

Сформулюйте математичну постановку задачі завантаження виробничої потужності. Економічна суть цільової функції та обмежень.

Суть симплекс-методу розв”язання задачі лінійного програмування. Економічна інтерпретація значень симплекс-таблиці розв”язку.

Загальна схема розв”язання задачі завантаження виробничої потужності в програмному забезпеченні Mathcad.

Загальна схема розв”язання задачі завантаження виробничої потужності в програмному забезпеченні Excel.

В чому полягає суть двоїстої задачі лінійного програмування?

Дата добавления: 2015-10-28