
Читайте также:
|
1. Вычислить интеграл  , рассматривая его как предел интегральной суммы.
, рассматривая его как предел интегральной суммы.
2. Оценить интеграл  .
.
3. Исходя из геометрического смысла определенного интеграла, найти: а)  ; б)
; б)  .
.
4. Исследовать сходимость интеграла  .
.
5. Вычислить  .
.
6. При каком а площадь, ограниченная линиями  и
и 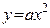 , равна
, равна  ?
?
7. Найти длину пространственной кривой 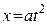 ,
,  ,
, 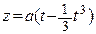 ,
,  .
.
8. Цепная линия  вращается вокруг оси абсцисс. При этом получается поверхность, называемая катеноидом. Найти объем тела, ограниченного катеноидом и двумя плоскостями, отстоящими от начала координат на а и b единиц и перпендикулярными к оси абсцисс.
вращается вокруг оси абсцисс. При этом получается поверхность, называемая катеноидом. Найти объем тела, ограниченного катеноидом и двумя плоскостями, отстоящими от начала координат на а и b единиц и перпендикулярными к оси абсцисс.
9. При гармоническом колебательном движении вдоль оси абсцисс около начала координат скорость ν дается формулой:  . Найти положение точки в момент времени t 2, если в момент времени t 1 она находилась в точке х = х 1.
. Найти положение точки в момент времени t 2, если в момент времени t 1 она находилась в точке х = х 1.
Ответы. Часть 1: 1. а) нет; б)нет; в) да. 2. 0. 3. а)  <
<  ; б)
; б)  <
<  .
.
4.  ,
, 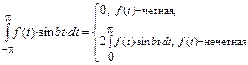 . 5. а)
. 5. а)  ; б)
; б)  ; в) ln2; г)
; в) ln2; г)  ; д)
; д)  ; е) 4-ln9; ж)
; е) 4-ln9; ж)  ; з)
; з)  . 6.
. 6.  7. а)
7. а)  ; б) расходится.
; б) расходится.
Часть2. 1 а)  б)3π а 2/2 2. а)ln3–0,5 б)12. 3. 24π. 4. 150кг 5. 2γ аb 2/3. 6. 135 дж
б)3π а 2/2 2. а)ln3–0,5 б)12. 3. 24π. 4. 150кг 5. 2γ аb 2/3. 6. 135 дж
вариант 4
Часть1
1. Используя теорему существования определенного интеграла, установить, существует ли определенный интеграл от данной функции по указанному промежутку:
а)  ; б);
; б);  в)
в)  .
.
2. Используя одно из свойств определенного интеграла, упростите вычисление интеграла  .
.
3. Не вычисляя, определить, какой из интегралов больше:
а)  или
или  ; б)
; б)  или
или  . Ответ обосновать.
. Ответ обосновать.
4. Чему равны выражения: 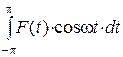 и
и 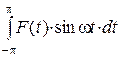 , если F (t)- четная функция; нечетная функция?
, если F (t)- четная функция; нечетная функция?
5. Вычислить:
а)  б)
б)  , в)
, в)  , г)
, г) 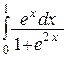 ; д)
; д)  ;
;
е)  ; ж)
; ж)  ,; з)
,; з) 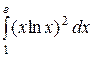 .
.
7. Вычислить  , если f (x) =
, если f (x) =  .
.
8. Вычислить интегралы, или установить их расходимость:
а)  б)
б)  , а > 0.
, а > 0.
Часть 2
1. Построить фигуру, ограниченную линиями, и найти ее площадь:
а) x × y = 4, x + y - 5 = 0; б) r = a(1+sinj).
2. Найти длину дуги кривой: а)  между точками пересечения ее с осью ОХ; б)
между точками пересечения ее с осью ОХ; б) 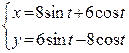 ,
,  .
.
3. Найти объем тела, полученного вращением вокруг оси OY фигуры, ограниченной линиями  . Сделать чертеж.
. Сделать чертеж.
4. Скорость тела, брошенного вертикально вверх с начальной скоростью ν 0, без учета сопротивления воздуха равна  , где t - протекшее время; g – ускорение свободного падения. На какую максимальную высоту поднимется тело?
, где t - протекшее время; g – ускорение свободного падения. На какую максимальную высоту поднимется тело?
5. Найти момент инерции относительно оси OX площади прямоугольника, ограниченного линиями x = 0, x = a, y = 0, y = b.
6. Вычислить работу, необходимую для выкачивания масла (плотность γ) из вертикального цилиндрического резервуара высотой Н и радиусом R.
Дата добавления: 2015-10-30; просмотров: 81 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дополнительные задачи | | | Дополнительные задачи. |