Тема 3. Задание и изображение поверхностей

Плоскость. Взаимное положение точки и плоскости,

Двух плоскостей

Вопросы

1. Запишите определитель каждой изображённой плоскости.

2. Как расположена каждая плоскость относительно П₁ и П₂?

3. Как расположена точка М относительно плоскости (принадлежит, не принадлежит, расположена выше, ниже, дальше, ближе по отношению к наблюдателю?

4.Запишите символически, как расположена прямая а относительно плоскости Ф?    

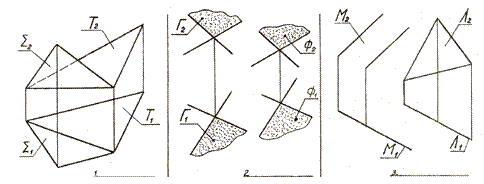5. Запишите символически, каково взаим-ное положение двух плоскос- тей – Σ и Τ, Γ и Ф, Μ и Λ.

Задачи 3.1.1. Через заданные точки провести плоскости указанного класса с помощью указанных определителей. В плоскости Σ построить горизонталь и фронталь.

а) Σ (a, b), где a ∩ b, б) Ф (a, М), об- в) Т (a, b), где a ∩ b, г) Ώ (А, В, С),

общего положения щего положения профильно - горизонталь-

проецирующую ную

3.1.2. Построить горизонтальную проекцию прямой m, принадлежащей плоскости Σ (a, b), где a|| b.

3.1.3. Построить горизонтальную проекцию точки М, принадлежащей плоскости Σ (a, b), где a|| b.

3.1.4. Построить проекции отрезка АВ, принадлежащего плоскости Σ (a, b), где a ∩ b.

3.1.5. Построить горизонтальную проекцию плоского пятиугольника АВСDE.

3.1.6. Через точку А провести прямую l, пересекающую прямую m и параллельную плоскости Т.

3.1.7. Через точку М провести плоскость Т, параллельную плоскости Σ (a, b), где a|| b.

3.1.8. Построить горизонтальную проекцию прямой с, принадлежащей плоскости Σ (а ∩ b).

3.1.9. Через точку К провести плоскость Т (m ∩ n), параллельную плоскости Σ (АВС).

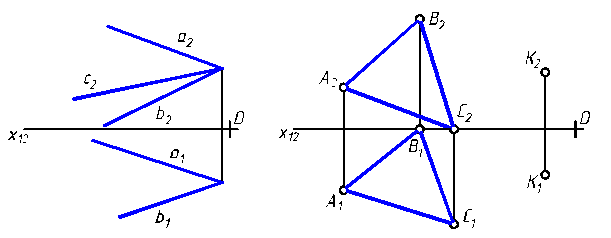3.1.10. Через точку К провести горизонтально-проецирующую плоскость Т, параллельную прямой n. Построить одно из положений горизонтальной проекции М₁ точки М, расположенной перед плоскостью Т.

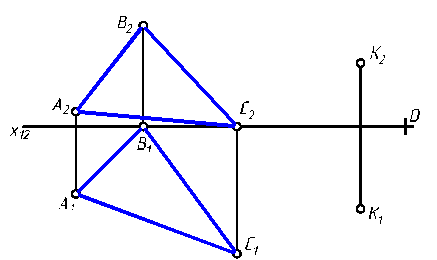
3.1.11. Через точку К провести фронтально-проецирующую плоскость Σ, параллельную фронтали, принадлежащей плоскости Т (АВС).

Задание на дом

3.1.12. Через точку К провести прямую d, пересекающую прямую m и параллельную плоскости Σ (АВС).

3.1.13. Определить, параллельна прямая n плоскости Σ (а ∩ b), или не параллельна.

3.1.14. Построить натуральную величину треугольника АВС при

помощи дополнительной плоскости П₄ ^ П₁.

3.1.15. Построить натуральную величину линии m при помощи дополнительной плоскости П₅ ^ П₂ .

Дата добавления: 2015-10-23