Многогранники и кривые поверхности

Вопросы

1. Каковы основные способы задания поверхностей? __________________

2. Что называется определителем поверхности? _______________________

3. Какая поверхность называется линейчатой? ________________________

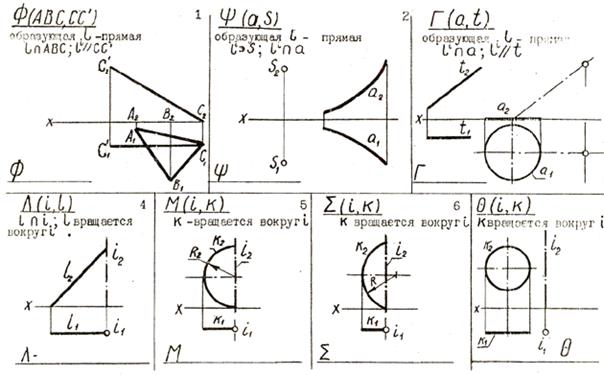
4. Напишите названия поверхностей, заданных определителями.

3.2.1. Построить недостающие проекции точек M, N и К, принадлежащих граням пирамиды.

3.2.2. Построить профильную проекцию призмы и недостающие проекции точек А, В и С.

3.2.7. Вписать в таблицу названия изображённых на рисунке элементов процесса вращения.

3.2.8. Точку А повернуть вокруг оси i на 90º по часовой стрелке.

3.2.9. Построить очерки проекций конической поверхности вращения Ω (l, i) и недостающие проекции точек М и N, расположенных на этой поверхности.

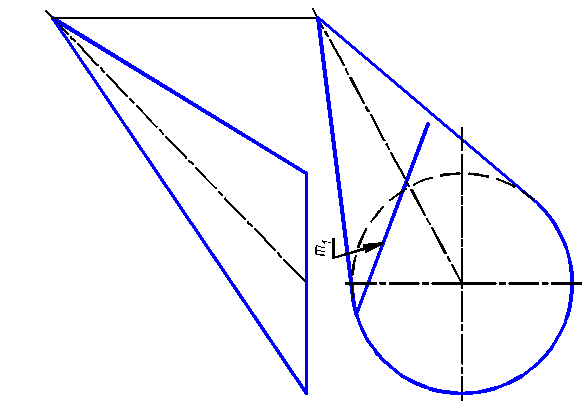
3.2.10. Построить недостающие проекции линии m, принадлежащей поверхности конуса вращения. Определить видимость линии m.

i₂

3.2.11. Построить очерки проекций сферы Ф (m, i). Построить недостающие проекции точек А и В, расположенных на сфере.

3.2.12. Построить очерки проекций тора Ф (b, i). Построить недостающие проекции точки К и линии n, расположенных на торе, и определить видимость.

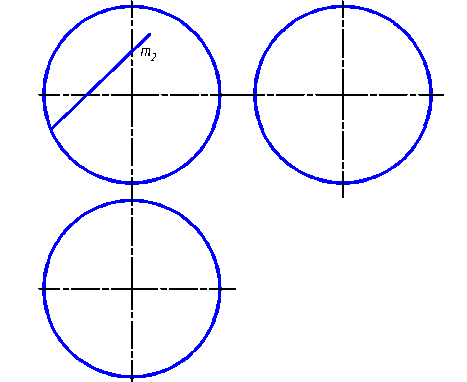
3.2.13. Построить недостающие проекции линии m, расположенной на сфере. Определить видимость этой линии.

3.2.14.Построить недостающие проекции точек К и М, принадлежащих поверхности тора, определить их видимость

3.2.15. Построить горизонтальную проекцию точки К и фронтальную проекцию линии m, принадлежащих поверхности тора. Определить их видимость.

3.2.16. Построить очерки проекций поверхности вращения Т (k, i). Построить горизонтальную проекцию точки М и фронтальную проекцию линии m, принадлежащих этой поверхности. Определить видимость точки М илинии m.

Задание на дом

3.2.17. Построить горизонтальные проекции цилиндра вращения с осью i и точек А и В, расположенных на поверхности цилиндра.

3.2.18. Построить фронтальную проекцию линии m, расположенной на поверхности тора. Определить видимость этой линии.

3.2.19. Построить очерки проекций поверхности однополостного гиперболоида Ф (i, l) и горизонтальную проекцию точки N, расположенной на этой поверхности.

3.2.20. Построить линии каркаса поверхности прямого геликоида Θ (i, l, h). Построить очерки проекций этой поверхности и проекцию точки N Θ.

3.2.21. Построить линии каркаса поверхности цилиндроида Т (а, b, Σ). Построить недостающие проекции точки N и линии m, расположенных на этой поверхности.

3.2.22. Построить линии каркаса поверхности гиперболического параболоида (косой плоскости) Ώ (а, b, П₁). Построить недостающие проекции точки К и линии m, расположенных на этой поверхности.

Дата добавления: 2015-10-23