Експериментальна частина. Схема лабораторної установки представлена на рис

Схема лабораторної установки представлена на рис. 1. Джерело струму 1 живить лампу розжарювання 4. Струм та напруга на лампі

Рисунок 5.1

фіксуються відповідно амперметром 2 та вольтметром 3, що розташовані на джерелі струму 1. Світло від лампи розжарювання відбивається від екрану 5 і потрапляє на термостовпчик 6, що генерує напругу, яка вимірюється міліамперметром 7.

5.3 Хід роботи

1. Перед тим як увімкнути джерело струму в мережу впевнимось, що потенціометр 8 джерела знаходиться у крайньому лівому положенні, при якому струм та напруга на лампі розжарювання дорівнюють нулю. Увімкнемо джерело струму в мережу і повільно обертаючи потенціометр джерела по годинній стрільці, встановимо максимальне значення струму через лампу 5А (не більше!).

2. Зачекаємо приблизно 1 хвилину поки в системі не встановиться стан рівноваги і мілівольтметр 7 покаже певне стале значення напруги, що генерується термостовпчиком 6.

3. Результати вимірів струму та напруги на лампі, а також напругу на термостовпчику занести в таблицю. Поступово зменшуючи струм через лампу, повторити виміри при значеннях сили струму в інтервалі від 5 до 1 амперу з кроком в 0,5 ампера. Після встановлення кожного нового значення струму напругу на термостовпчику - записувати не раніше ніж через 1 хвилину для того, щоб система була в змозі прийти в стан рівноваги. Данні вимірювань занести в таблицю 5.1.

Таблиця 5.1

№	I,A	U, B	R, Ом	t, ^0C	T,K	u, мВ	ln T	ln u
	4,5
	3,5
	2,5
	1,5

4. Для кожної пари значень сили струму та напруги визначити по закону Ома опір нитки накалу лампи розжарювання

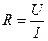. (5.8)

Данні занести в таблицю 5.1.

5. Опір лампи розжарювання пов'язаний з температурою її нитки формулою:

, (5.8)

де - опір при ; - температурний коефіцієнт опору, який дорівнює: ; - температура по шкалі Цельсія.

З формули (5.8) знаходимо температуру нитки лампи в градусах Цельсія

(5.9)

і абсолютну температуру за формулою

(5.10).

6. Напруга, що виникає в термостовпчику практично лінійно залежить від енергетичної світимості нитки, тобто можна вважати, що

, (5.11)

де - певна стала величина. З іншого боку згідно закону Стефана-Больцмана енергетична світимість пропорційна четвертому ступеню температури. Для перевірки цього факту, користуючись формулами (5.6) та (5.11) для енергетичної світимості запишемо:

. (5.12)

Після логарифмування формули (12) одержуємо:

, (5.13)

де - певна стала величина.

Візьмемо логарифми від напруги , та температури . Данні занесемо в таблицю.

7. Побудуємо графік залежності від 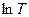(рис.5.2).

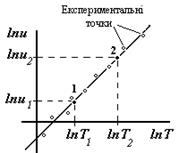
Рисунок 5.2

8. Користуючись побудованим графіком, визначимо показник . Для чого виберемо на графіку (але не з таблиці!) дві будь-які довільні точки і розрахуємо за формулою:

. (5.14)

Порівняймо одержане значення з показником ступеня в законі Стефана-Больцмана.

Контрольні запитання

1. Яке випромінювання називається тепловим?

2. Що таке енергетична світимість?

3. Що таке густина енергетичної світимості?

4. Як пов’язані між собою енергетична світимість і густина енергетичної світимості?

5. Яке тіло називається абсолютно чорним?

6. В чому полягає закон Стефана-Больцмана?

Література

1. Ландcберг Г. С. Оптика. – М.: Наука, 1976.- с. 682 – 698.

2. Сивухин Д. В. Общий курс физики. – т. 4. – М.: Наука, 1980.- с. 685 – 687.

3. Савельев И. В. Курс общей физики.– т. 3. – М.: Наука, 1982.- с. 16 – 18.

6 ЛАБОРАТОРНА РОБОТА № 66. ПОБУДОВА ДИСПЕРСІЙНОЇ КРИВОЇ МОНОХРОМАТОРА УМ-2

Мета роботи - Побудувати дисперсійну криву монохроматора УМ-2 по відомим довжинам хвиль лінійчатого спектра ртуті.

Прилади і обладнання: Монохроматор УМ-2, ртутна лампа, джерело живлення ЕПС-2.

Дата добавления: 2015-10-29