
Читайте также:
|
На рис. 7 представлены направления векторов линейной скорости  , угловой скорости
, угловой скорости  и псевдовектора угла поворота
и псевдовектора угла поворота  при вращательном движении
при вращательном движении
 Рис.7
Рис.7
На рис.8 представлены направления векторов линейной скорости  , тангенциального
, тангенциального  , нормального
, нормального  и полного
и полного 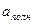 ускорений в случае равноускоренного (рис.8а) и равнозамедленного (рис.8б) вращательных движений.
ускорений в случае равноускоренного (рис.8а) и равнозамедленного (рис.8б) вращательных движений.


а) Рис. 8 б)
КИНЕМАТИКА
| Поступательное движение | Вращательное движение | |
 путь путь
 линейная скорость линейная скорость 
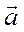 - ускорение - ускорение
 
 равноускоренное ( равноускоренное ( )
равнопеременное ( )
равнопеременное ( ) )


| 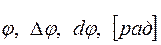 угол поворта
угловая скорость угол поворта
угловая скорость  
 - угловое ускорение - угловое ускорение
 
 равноускоренное ( равноускоренное ( )
равнопеременное ( )
равнопеременное ( ) )


| |
Связь линейной и угловой скорости
 Связь тангенциального и углового ускорений
Связь тангенциального и углового ускорений

 
| ||
| Динамика | ||
Поступательное движение
Инертные свойства - масса

 Основное уравнение динамики поступательного движения
Основное уравнение динамики поступательного движения  
 
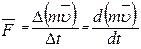 производная импульса определяет действующую силу
Кинетическая энергия при поступательном движении
производная импульса определяет действующую силу
Кинетическая энергия при поступательном движении
 

| Вращательное
Инертные свойства – момент инерции

  , , 
 Момент силы направлен вдоль оси вращения по правилу правого винта (смотри рисунок ниже)
Момент силы направлен вдоль оси вращения по правилу правого винта (смотри рисунок ниже)
 Основное уравнение динамики вращательного движения
Основное уравнение динамики вращательного движения
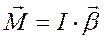  Момент импульса
Момент импульса
   
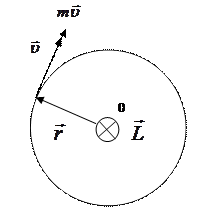
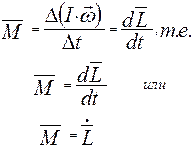 Уравнение моментов (производная момента импульса определяет вращающий момент силы) Уравнение моментов (производная момента импульса определяет вращающий момент силы)
  Кинетическая энергия при вращательном
движении
Кинетическая энергия при вращательном
движении
  Плоское движение (тело катится)
Плоское движение (тело катится)
 
| |
Работа при поступательном движении
 
| Работа при вращательном движении
 
| |
Момент инерции твердого тела относительно данной оси можно трактовать как количественную меру инертности тела относительно этой оси.
Здесь следует отметить, что некоторые студенты ошибочно считают момент инерции мерой инертности тела при вращательном движении твердого тела относительно данной оси. В действительности же, момент инерции тела относительно данной оси существует независимо от того, вращается ли данное тело или нет. При вращательном движении твердого тела мы наблюдаем одно из частных, конкретных проявлений этого свойства инертности, так же как, например, масса тела, существуя независимо от характера движения тела, играет роль инертности тела при его поступательном движении.
В тех случаях, когда дискретностью вещества можно пренебречь, считают, что в объеме твердого тела вещество распределено непрерывно. Это позволяет при вычислении момента инерции тела использовать интегральное исчисление.
Твердое тело “разбивают” на элементарно малые участки объемом dV, такие, что их можно считать материальными точками. Распределение вещества внутри объема тела можно характеризовать величиной
 ,
,
которая называется плотностью в малой окрестности dV данной точки тела.
Выразив элементарную массу dm с помощью  , определение запишем в виде
, определение запишем в виде
 ,
,
где суммирование по всем материальным точкам заменено интегрированием по объему твердого тела. В соотношении) величина  определяет расстояние от элементарного объема dV до оси, относительно которой вычисляется момент инерции тела. В общем случае величины
определяет расстояние от элементарного объема dV до оси, относительно которой вычисляется момент инерции тела. В общем случае величины  и R являются функциями положения элементарного объема
и R являются функциями положения элементарного объема  (например, декартовых координат x, y, z). Для однородного тела
(например, декартовых координат x, y, z). Для однородного тела  и поэтому вычисление момента инерции тела упрощается:
и поэтому вычисление момента инерции тела упрощается:
 . Видно, что величина момента инерции тела относительно данной оси существенным образом зависит не столько от общей массы тела, сколько от того, как эта масса распределена относительно данной оси.
. Видно, что величина момента инерции тела относительно данной оси существенным образом зависит не столько от общей массы тела, сколько от того, как эта масса распределена относительно данной оси.
· Момент инерции характеризуется инертные свойства тел при вращательном движении.
· Момент инерции характеризуется распределение массы относительно оси вращения
· Момент инерции – величина аддитивная (ее можно суммировать и вычитать)
· Момент инерции твердого тела любой формы относительно неподвижной оси Z вычисляется по формуле:

Вычислим моменты инерции нескольких однородных тел простейшей формы
1. Момент инерции однородного цилиндра




2. Момент инерции полого цилиндра


 Для тонкого цилиндра
Для тонкого цилиндра 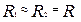

2. Момент однородного стержня относительно оси Z


3. Момент инерции шара относительно центра масс.

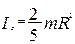
4. Теорема Штейнера
 с-центр масс
с-центр масс
m-масса

Момент импульса.
1. Момент импульса относительно точки О






- момент импульса относительно точки
2. Момент импульса относительно неподвижной оси Z Z'








 - момент импульса относительно произвольной оси = произведению угловой скорости на момент инерции тела относительно этой же оси (величина скалярная).
- момент импульса относительно произвольной оси = произведению угловой скорости на момент инерции тела относительно этой же оси (величина скалярная).
Основное уравнения динамики вращательного движения твердого тела.
Продифференцируем выражение для момента импульса

Скорость изменения момента импульса равна моменту сил, приложенных к телу.

Получили, что момент силы = моменту инерции, умноженному на угловое ускорение
 -- основное уравнение динамики вращательного движения твердого тела. Проведем сравнение формул основного уравнения динамики поступательного и вращательного движений:
-- основное уравнение динамики вращательного движения твердого тела. Проведем сравнение формул основного уравнения динамики поступательного и вращательного движений:




Дата добавления: 2015-10-23; просмотров: 207 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основы кинематики и динамики вращательного движения твердого тела. Законы сохранения | | | Определение модуля кручения пружины D |