Медианы треугольника и тетраэдра

Теорема 3. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

Доказательство. Пусть медианы АD и ВЕ пересекаются в точке О (рис. 3). Построим четырехугольник MNDE, где М и N – середины отрезков АО и ВО. Тогда MN || AB и MN = 0,5AB как средняя линия треугольника АОВ; ED || AB и ED = 0,5AB как средняя линия треугольника АВС. Поэтому MN || ED и MN = ED, т. е. фигура MNDE – параллелограмм с диагоналями MD и NE. Значит, МО = ОD і так как МО = АМ, то АМ = МО = ОD. Следовательно, точка О делит медиану АD отношении АО;ОD = 2:1 и в таком же отношении эта точка делит медиану ВЕ.

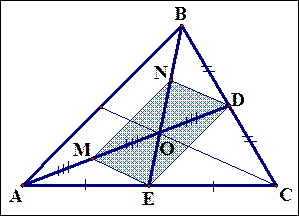
Рис. 3

Очевидно, что в том же отношении должна делить и третью медиану точка ее пересечения как с первой, так и со второй медианами. При этом третья медиана не может пересечь их в точках, отличных от О, поскольку тогда на каждой медиане имелись бы две различные точки, делящие ее в отношении 2:1, считая от вершины, что невозможно. Теорема 3 доказана.

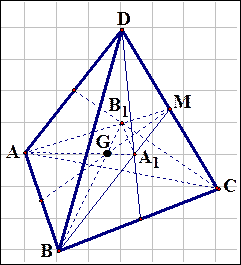
Рис. 4

Назовем медианой тетраэдра отрезок, соединяющий вершину тетраэдра с центроидом противолежащей грани. Оказывается, для медиан тетраэдра справедлива теорема 4, аналогичная теореме 3.

Теорема 4. Четыре медианы тетраэдра пересекаются в одной точке и делятся ею в отношении 3:1, считая от вершины.

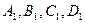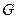Доказательство. Вершины А, В, С, D тетраэдра АВСD (рис. 4) соединены отрезками с центроидами (точками пересечения медиан) его граней ВСD, СDА, DАВ, АВС. Докажем, что отрезки имеют общую точку (центроид тетраэдра), которая делит каждый из этих отрезков в отношении 3: 1. Пусть отрезк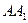и и 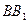пересекаются в некоторой точке 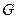(рис. 4). Тогда . Далее используя теорему, обратную теореме Фалеса получаем: АВ || 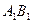. Отсюда следует подобие треугольников АМВ и 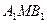(коэффициент их подобия АМ: 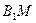= 3:1). Тогда подобны треугольников АGB и с тем же коэффициентом подобия. Значит, 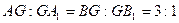. Очевидно, что в том же отношении должна делить и третью (четвертую) медиану точка ее пересечения как с первой, так и со второй медианами (по аналогии с теоремой 3). При этом третья (четвертая) медиана не может пересечь их в точках, отличных от О, поскольку тогда на каждой медиане имелись бы две различные точки, делящие ее в отношении 3:1, считая от вершины, что невозможно. Теорема 4 доказана.

Заметим, что отрезки, соединяющие середины противоположных ребер тетраэдра, проходят через центроид 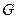и делятся им пополам. Для доказательства следуетрассмотреть трапецию и учесть, что середины ее оснований, точка пересечения ее диагонале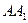й и 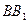и точка пересечения продолжений боковых сторон 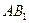и 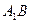расположены на одной прямой.

Дата добавления: 2015-10-29