Пары аналогичных утверждений

В каждой паре пункт а) – некоторая теорема планиметрии, а в пункте б) – ее пространственный аналог.

1. а) Площадь треугольника, описанного около окружности, вычисляется по формуле , где радиус этой окружности, 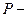периметр треугольника.

б) Объем тетраэдра, описанного около сферы, вычисляется по формуле , где радиус этой сферы, полная поверхность тетраэдра.

2. а) Если в треугольник вписана окружность с радиусом ,

то , где высоты треугольника.

б) Если в тетраэдр вписана сфера с радиусом ,

то , где высоты тетраэдра.

3. а) Через центр правильного треугольника проведена прямая, параллельная основанию. На этой прямой внутри треугольника взята произвольная точка О. Докажите, что расстояние от точки О до основания треугольника равно среднему арифметическому расстояний от точки О до боковых сторон треугольника.

б) Через центр правильного тетраэдра проведена плоскость, параллельная основанию. На этой плоскости внутри тетраэдра взята произвольная точка О. Докажите, что расстояние от точки О до основания тетраэдра есть среднее арифметическое расстояний от точки О до боковых граней тетраэдра.

Чтобы доказать определенное утверждение в стереометрии, часто полезно обратиться к более простой аналогичной теореме планиметрии. Происходит обобщение плоского случая на пространственный. В качестве примера приведем еще две такие пары аналогичных утверждений. Расположим их параллельно:

Планиметрия	Стереометрия
Если две прямые на плоскости пересекаются тремя параллельными прямыми, то соответствующие отрезки пропорциональны.	Если две прямые в пространстве пересекаются тремя параллельными плоскостями, то соответствующие отрезки пропорциональны.
Диагонали параллелограмма пересекаются в их общей середине.	Четыре диагонали параллелепипеда имеют общую точку, являющуюся серединой каждой из них.

Заключение

Таким образом, мы установили, что гораздо легче и естественней постигать связи и выводить утверждения для пространственных фигур, пользуясь аналогичными плоскими примерами и конструкциями. Мы провели аналогию геометрических понятий, исследовали пары аналогичных утверждений в планиметрии и стереометрии: свойство биссектрисы треугольника и свойство биссектора двугранного угла тетраэдра; свойство медиан треугольника и медиан тетраэдра; соотношение между радиусом вписанной окружности в треугольник и его тремя высотами на плоскости и соотношение между радиусом вписанной сферы в тетраэдр и его четырьмя высотами в пространстве; формула площади треугольника, описанного около окружности, и формула объема тетраэдра, описанного около сферы. Во многих случаях доказательство может быть прямо распространено с плоскости на пространство. Это дает возможность лучше вникнуть во взаимоотношения, существующие между плоской и пространственной геометрией.

Список использованной литературы

1. Кот, В. И. Как одолеть олимпиадные задачи по математике: Пособие для учителей общеобразовательной школы/В. И. Кот – Мн.: «Бестпринт», 2002. – 400 с.

2. Кот, В. И. Развитие исследовательской деятельности учащихся / В. И. Кот // Хрустальная Альфа: сборник материалов IV межрегиональной научно-практической конференции: в 2-х ч.: часть 1: работы преподавателей ВУЗов и учителей. – Гродно: УО “Гродненский ГОИПК и ПРР и СО”. – 2006. – С. 53 – 57.

Дата добавления: 2015-10-29