Биссектриса и биссектор

Геометрические аналогии

Роман Рафалович, учащийся 10 «А» класса ГУО «Ивьевская средняя школа»

( Научный руководитель – Кот В. И., кандидат педагогических наук)

Содержание

Введение………………………………………………………………….............1

Основная часть

1. Биссектриса и биссектор….…………………………………........................1

2. Медианы треугольника и тетраэдра……………………………………….2

3. Площади и объемы…………………....………………………………...........4

4. Пары аналогичных утверждений…………………………………………..5

Заключение………………………………………………………………………6

Список использованной литературы………………………...........................7

Введение

Изучая геометрию, можно заметить, что некоторые свойства треугольника и тетраэдра похожи, а многие геометрические понятия, связанные с треугольником, имеют пространственные аналоги. Например, сторона треугольника – грань тетраэдра, длина стороны – площадь грани, вписанная окружность – вписанная сфера, описанная окружность – описанная сфера площадь – объем, биссектриса угла – биссектор двугранного угла и т. п. Понятию плоской геометрии параллелограмм аналогично понятие пространственной геометрии параллелепипед, прямоугольнику – прямоугольный параллелепипед, квадрату – куб и т. д.

Эта аналогия – не только внешняя. Многие теоремы о треугольниках, если заменить в их формулировках планиметрические термины соответствующими стереометрическими и соответствующим образом «подправить» формулировки, превращаются в теоремы о тетраэдрах. В данной работе мы рассмотрим пары таких теорем. В каждой паре первая теорема – некоторая теорема планиметрии, вторая – ее пространственный аналог.

Биссектриса и биссектор

Теорема 1. Биссектриса СD внутреннего угла треугольника АВС делит противолежащую сторону на отрезки, пропорциональные его сторонам АС и ВС.

Доказательство. Примем сначала за основания треугольники ADC и DCB (рис. 1) отрезки АС и ВС соответственно. Точка D равноудалена от сторон угла АСВ, поэтому .

Рис.1

Теперь примем за основания этих же треугольников отрезки AD и DB. Ясно, что 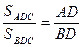. Следовательно, 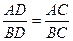, что и требовалось доказать.

Биссектором двугранного угла называется полуплоскость, делящая его на два равных по величине двугранных угла. Биссектор двугранного угла является множеством точек, равноудаленных от его граней. Докажем свойство биссектора двугранного угла тетраэдра (теорема 2), аналогичное свойству биссектрисы угла треугольника (теорема 1).

Теорема 2. Биссектор двугранного угла тетраэдра делит противолежащее ребро в отношении, равном отношению площадей граней, образующих этот двугранный угол.

Доказательство. Пусть ADM – сечение тетраэдра АВСD биссектором двугранного угла с ребром АD (рис. 2). Объемы тетраэдров АСМD и АВМD обозначим через и соответственно. Так как точка М одинаково удалена от граней АDС и АDВ, то .

С другой стороны, легко видеть, что . Поэтому . Следовательно, теорема 2 доказана.

Рис. 2

Попутно заметим, что , что еще раз подчеркивает аналогичность теорем 1 и 2.

Дата добавления: 2015-10-29