Определение физико-механических характеристик провода

Согласно [1, табл.2.5.8] для провода АС 300/39 с отношением 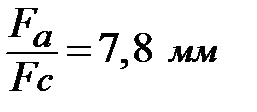температурный коэффициент линейного расширения , модуль продольной упругости .

Согласно [1, табл.2.5.7]:

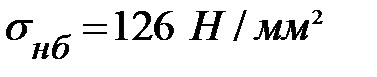- механическое напряжение при воздействии на провод наибольшей удельной механической нагрузки ,

- механическое напряжение при воздействии на провод низшей температуры t_,

- механическое напряжение при воздействии на провод среднегодовой температуры tсг.

Составим и решим основное уравнение состояния провода для двух вариантов. В каждом из вариантов искомыми будут среднеэксплуатационные значения среднеэксплуатационного механического напряжения.

Вариант 1: Исходные условия – возникновение наибольшей удельной нагрузки, искомые условия – среднеэксплуатационные, тогда уравнение состояния примет следующий вид:

Полученное уравнение можно представить как неполное кубическое:

Решим неполное кубическое уравнение методом Ньютона:

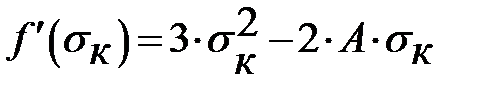- производная функции.

Определим, как изменится напряжение в проводе в зависимости от изменения длины пролета при возникновении наибольшей удельной нагрузки.

При :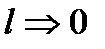

При :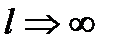

Таким образом, среднеэксплуатационное механическое напряжение при условии возникновения наибольшей удельной нагрузки будет изменяться в пределе от 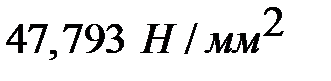до .

Получим зависимости А и В от li.

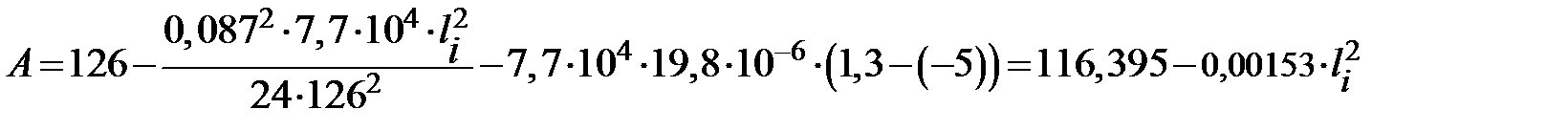
Вычислим значения А и В, а также значения механического напряжения при длинах пролетов от 100 м до 470 м. Результаты расчетов представлены в таблице 4.4.

Таблица 4.4-Результаты расчета уравнения состояния провода для первого варианта

L	A	B	sigma0	sigma1	sigma2	sigma3	sigma4
	116,395		116,395	116,395	116,395	116,395	116,395
	101,099		107,642	104,49685	104,3108	104,3102	104,3102
	81,979		94,761	91,588971	91,39155	91,3908	91,3908
	55,211		87,552	79,441106	78,15048	78,11924	78,11922
	20,795		82,292	70,568126	68,11381	68,01141	68,01123
	-21,269		78,542	64,75013	61,7341	61,59661	61,59633
	-70,981		75,854	60,981884	57,81524	57,67735	57,67709
	-128,34		73,895	58,468772	55,31704	55,18932	55,18911
	-221,493		71,962	56,188824	53,13629	53,02363	53,02347

Вариант 2: Исходные условия наинизшая температура окружающей среды; искомые условия – среднеэксплуатационные, тогда уравнение состояния примет вид:

Исследуем, как изменится напряжение в проводе в зависимости от изменения длины пролета при возникновении наибольшей удельной нагрузки.

При :

При

Таким образом, среднеэксплуатационное механическое напряжение при условии возникновения наибольшей удельной нагрузки будет изменяться в пределе от до .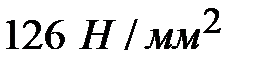

Зависимости А и В от длины пролета :

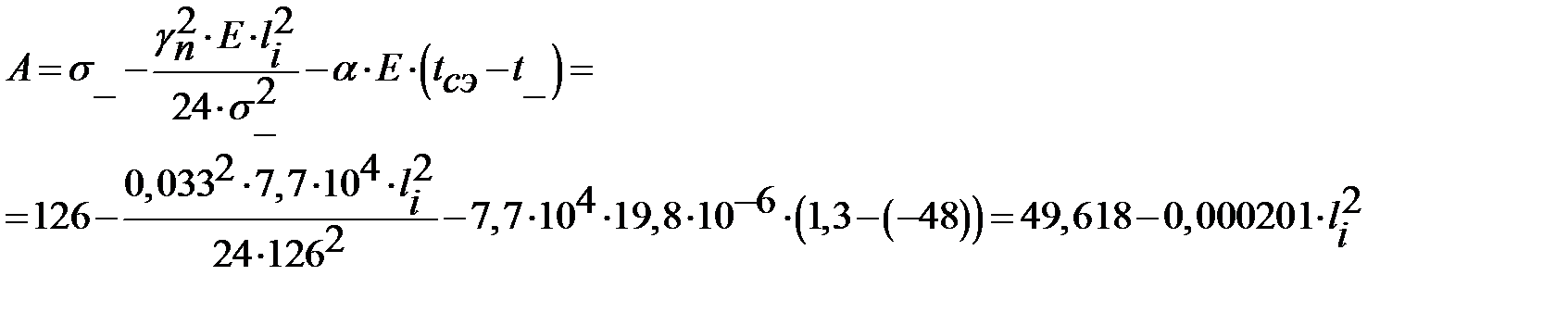
Вычислим значения А и В, а также значения механического напряжения при длинах пролетов от 100 м до 470 м. Результаты расчетов представлены в таблице 4.5.

Таблица 4.5 -Результаты расчета уравнения состояния провода для второго варианта

L	A	B	sigma0	sigma1	sigma2	sigma3
	49,618		49,618	49,618	49,618	49,618
	47,417		92,012	71,463	61,179	58,125
	44,666		92,66	73,584	65,521	63,967
	40,815		93,527	76,258	70,344	69,645
	35,863		94,577	79,275	75,139	74,846
	29,811		95,771	82,447	79,646	79,528
	22,659		97,071	85,627	83,768	83,721
	14,406		98,438	88,708	87,489	87,47
	1,003		100,403	92,739	92,068	92,064

Зависимости напряжений в проводе от длины пролета представлены на рисунке 4.1.

Рисунок 4.1 – Зависимости напряжений в проводе от длины пролета

Дата добавления: 2015-10-23