Магнит өрісінің кернеулігі. Индукция векторы.

Интеграл астында жақшалар ішінде орналасқан шама H әрпімен белгіленеді және магнит өрісі кернеулігі деп аталады.

L контурмен қамтылатын өткізгіштік токтардың алгебралық қосындысын ток тығыздығынан L контурына тірелген S_L бет арқылы алынған ағын түрінде жазуға болатынын еске алсақ осы өрнекті былай жазуға болады: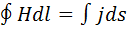

Сонымен магниттердегі магнит өрісін сипаттау үшін тек өткізгіштік токтармен анықталатын магнит өрісі кернеулігі деген физикалық шама кіргізуге болады екен. Осы өрнек магниттердегі магнит өрісі үшін ток заңы болып табылады. Егер магнит өрісін сипаттайтын векторларды электр өрісін сипаттайтын векторлармен салыстырсақ, магнит өрісінің кернеулігі Н электр өрісі ығысу векторына D, ал магнит өрісі индукциясы векторы В электр өріс кернеулігіне Е ұқсас шамалар. Бұл шамалардың арасында өзара сәйкестіктің болмауы электрлік және магниттік құбылыстарды зерттеудің бастапқы кезінде солай аталып кетуіне байланысты.

Ендігі жерде магнит өрісі индукциясының векторы туралы қарастырайық. Жіңішке шексіз ұзын токтың тудыратын магнит өрісі индукциясының өрнегін пайдаланып, магнит өрісі индукциясы векторынан тұйық контур бойынша алынған интегралдың неге тең екенін анықталық:

Интеграл алынатын контур ретінде жіңішке шексіз ұзын токты қамтитын кез-келген тұйық L контурды алуға болады.

Токтан r қашықтықтағы контур нүктесінде алынған dl элементі екі құраушыға жіктеуге болады: бірі токқа парллель dl_ll, екіншісі токқа перпендикуляр болғандықтан, және Осы қатынастарды ескерсек,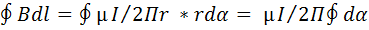

Тоқты қамтитын кез келген тұйық контур бойымен алган кезде α бұрышы ылғида бір жаққа қарай айналады толық бір айналыс жасағанда α бұрышының өзгеруі 2Π-ге тең болады:

Ендеше,

Егер L контур бірнеше тоқты қамтитын болса,суперпозиция принципін пайдаланып,осы өрнектіктің орнына: екенін табамыз.Бұл өрнектің сол жагында L контурмен қамтылатын тоқтардың алгебралық қосындысы тұр.Оң тоқ ретінде контур бойымен интегралдау бағыты ток бағытымен оң бұранда ережесімен байланысқан токты алады,ал қарама қарсы бағыттағы токты теріс деп алу керек.Алынған контурмен қамтылған токтардың алгебралық қосындысын ток тығыздықтары арқылы жазуға болады.Егер L контурға тірелген S бет алсақ, бұл бет токтар жүріп тұрған өткізгіштермен S₁ ,S₂,… S_n беттер бойымен қиылысады.Олай болса, .

Соңғы өрнектің оң жағын ток тыгыздыгынын L контурға тірелген S бет бойымен алынған ағыны ретінде жазуға болады, себебі ток жоқ жерлерде өткізгіштің көлденең қималары S бетпен қиылыспайтын жерлерде интеграл нольге теі, яғни Сондықтан

Егер L контур токты қамтымайтын болса, себебі контур бойымениайнала интеграл алған кезде радиалдық түзу бір жаққа қарай, одан кейін екінші жаққа айналады. Бірінші бөлікті айналған кезде α бұрышының өзгеруі α₁₂ екінші бөлікті айналған кездегі α бұрышының өзгеруі α₂₁ шамасы жағынан тең, бірақ таңбасы қарама-қарсы болады, яғни

6-сурак. Био-Савар Лаплас заңы. Био және Савар 1820 жылы формасы әртүрлі токтардың магниттік өрісіне зерттеу жүргізді.Олар магнит индукциясы, барлық жағдайда магнит өрісін туғызатын ток күшіне пропорционал және азды-көпті түрде И анықталатын нүктеге дейінгі ара қашықтыққа да байланысты болатынын анықтаған. Био және Савардың экспериментальды мәліметтеріне анализ жасай отырып, Лаплас кез келегн токтың магнит өрісін, токтардың жеке элементар учаскелерінің тудырған өрісінің векторлық қосындысы (суперпозиция) ретінде есептеуге болатынын тапты. Ұзындығы dl ток элементінің тудыратын өріс магнит индукциясы үшін Лаплас мына формуланы алды:

(1)

Мұндағы к’ – пропорционалдық коэффициенті, ол өлшем бірліктерін таңдап алуға байланысты, i- ток күші, dl – вектор, элементар ток учаскесімен және токтың өту бағытына сәйкес келетін вектор, r – элемент пен dB анықталатын нүктені қосатын

вектор,r-осы вектордың модулы. (1) қатысын Био-Савар-Лаплас немесе Био-Савар заңы дейміз. dB векторы dl және өріс есептелетін нүкте арқылы өтетін жазықтыққа перпендикуляр бағытталған: сонымен қатар dB бағытында dl-дің айналуы оң бұранда ережесімен dl-мен байланысты. dB модулі үшін мына өрнекті жазуға болады:

(2)

dB=k’

мұндағы α-dl және r векторлары арасындағы бұрыш. Био-савар заңы рационализациялық формада былай жазылады:

dB= (3)

яғни k= 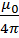. Магнит индукциясының СИ системасындағы бірлігі тесла (тл) деп аталады.

Біз білетіндей, электр тогы зарядтардың реттелген қозғалысы. Ендеше қозғалыстағы зарядтар магнит өрісін тудырады. (1) өрісі dl ток элементіндегі зарядтардың қозғалысынан туады. Қозғалыстағы бір зарядтың тудырған өрісінің магнит индукциясын табу үшін (1) өрнегіндегі i ток үшін токтың j тығыздығы мен өткізгіштің S көлденең қимасының көбейткіші арқылы алмастыра отырып түрлендіру жасаймыз. Ток тығыздығының j векторы мен dl векторының бағыттары бірдей. Сондықтан былай жазуға болады:

idl=Sjdl (4)

Егер өткізгіштегі барлық заряд тасымалдаушылары бірдей әрі e’ заряды болса десек (e’-алгебралық шама), онда токтың тығыздық векторын мынадай түрде қарастыруға болады:

j=e’nu (5)

мұндағы n-бірлік көлеміндегі заряд тасушылардың саны, u-олардың реттелген қозғалысының орташа жылдамдығы. Ток тасымалдаушылары оң болғанда j мен u-дың бағыттары бірдей болады. Тасымалдаушылар теріс болған жағдайда j мен u-дың бағыты бір-біріне қарама-қарсы болады.

(1) формуласына idl-ге арналған (4) өрнекті қойып, ондағы j-ді (5) –ге сәйкес ауыстырсақ (k'-ны μ₀/4π-ге тең деп алайық), нәтижесінде мынаны аламыз:

dB= (6)

Sdln көбейтіндісі ұзындығы dl өткізгіш элементіндегі заряд тасушыларының санын береді. (6) өрнекті осы санға бөліп, u жылдамдықпен қозғалатын бір зарядтың туғызған өрісінің магнит индукциясын аламыз.

Егер e’ заряды v жылдамдықпен қозғалса, онда магнит өрісінің осы заряд тудырған индукциясы, орны осы зарядқа қатысты нүктеде r радиус-вектормен анықталады, ол мынаған тең:

(7)

Гаусс системасында бұл формула мына түрде болады:

(8)

Кеңістікте электромагниттік ұйытқудың шекті жылдамдығы с жарық жылдамдығына тең жылдамдықпен тарайтынын еске ұстаған жөн. Сондықтан кеңістіктің берілген нүктесіндегі өріс, зарядтың τ=r/c секунд уақыттан бұрынғы күйіне сәйкес келеді. Сөйтіп, неғұрлым өрістің осы берілген нүктесі өріс тудырған зарядтан қашықтаған сайын өрістің мәнінің кешігуі соғұрлым көбірек болады. Егер зарядтың τ (υτ-ға тең болатынын) уақытын берілген нүктеге дейінгі r аралыққа қатысты орын ауыстыруын елемейтін болсақ, яғни υτ
≤r шартын сақтасақ, (7) және (8) формуласы дұрыс нәтиже береді. Осы теңсіздікті τ-ға бөліп, =c екенін ескерсек,

υ≤c (9)

шартын аламыз. Бұл жағдайда (7) және (8) формулалары орындалады.

Дата добавления: 2015-10-29