Синтез цифрових коректуючих пристроїв

Під час розробки цифрових систем керування зручно використовувати метод синтезу, що базується на логарифмічних частотних характеристиках. Передаточна функція розімкнутої ЦС є добутком дискретних передаточних функцій приведеної безперервної частини і цифрового регулятора: Якщо перейти до логарифмічних характеристик, як функцій абсолютної псевдочастоти l, то можна записати:

(3.79)

де - амплітудні логарифмічні характеристики розімкнутої системи, приведеної безперервної частини і цифрового регулятора.

Звідси ЛАЧХ цифрового регулятора:

(3.80)

Як зауважувалось раніше за умови wТ₀ < 2 псевдочастоту l можна замінити дійсною частотою w, тому для низьких частот (w < 2/Т₀) побудова ЛАЧХ і ЛФЧХ дискретної системи зводиться по суті до побудови відповідних характеристик початкової (не приведеної) безперервної частини системи з передаточною функцією

Розглянемо побудову логарифмічних характеристик у зоні високих частот (при w > 2/Т₀). Якщо сталі часу передаточної функції такі, що всі частоти спряження асимптотичної ЛАЧХ лежать ліворуч від частоти w = 2/Т₀ і ЛАЧХ при цій частоті має нахил (-20×n) дБ/дек, то високочастотна частина ЛАЧХ апроксимується інтегруючою ланкою 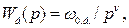де - базова частота високочастотної частини ЛАЧХ, яка визначається як частота перетину її першої асимптоти з віссю нуля децибел (горизонтальною віссю) (рис. 3.17).

Нехай, наприклад, низькочастотна частина ЛАЧХ на частоті w = l = 2/Т₀ має нахил –60 дБ/дек (тобто n=3). Тоді і, коли імпульсний елемент є екстраполятором нульового порядку, дискретна передаточна функція має вигляд:

(3.81)

За даними таблиці 3.1 отримуємо:

Виконуємо w-перетворення:

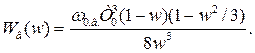
Переходимо до частотної функції:

(3.82)

Високочастотну частину ЛАЧХ, побудовану за виразом (3.82), наведено на рис. 3.17 праворуч від лінії l=2/Т₀: на частоті l=2/Т₀ нахил ЛАЧХ змінюється на +20дб/дек, а на частоті - на +40 дБ/дек, оскільки передавальна функція W_в(jl) у чисельнику містить дві ланки з однаковою сталою часу .

Збіг ЛАЧХ для дискретної передаточної функції безперервної частини системи в зоні низьких частот дає можливість виконувати синтез корегуючих пристроїв (цифрових регуляторів) відомими методами синтезу корегуючих пристроїв неперервних систем і використовувати розроблені для них номограми, графіки і таблиці.

Внаслідок синтезу методом ЛАЧХ знаходять ЛАЧХ корегуючого пристрою L_к(l) і за її виглядом визначають комплексну частотну функцію W_к(jl). Після цього виконують підстановку:

, (3.83)

визначають дискретну передаточну функцію W_к(z), а потім різницеве рівняння корекції, яке реалізується цифровим регулятором.

Дата добавления: 2015-10-29