
Читайте также:
|
База даних Kyiv-91.sav.
1. Дослідницьке запитання: “Чи ставлення респондентів до посилення в країні контролю за виконанням трудової дисципліни, включаючи перевірку громадян на вулицях у робочий час (v133), залежить від рівня їхньої освіти (v167)?”.
2. Програмуємо таблицю кростабуляцій з одночасним проведенням тесту χ2.
Підготовча дія: визначаємо, яка змінна має меншу кількість категорій, а яка – більшу (v133 – 3; v167 – 4). Analyze – Descriptive Statistics – Crosstabs. До колонок переводимо v133, до рядків – v167. Statistics – Chi-square – Continue. Cells – Counts: Observed, Expected – Percentages: Row – Residuals: Unstandardized – Continue – OK.
3. Аналізуємо таблицю:

3.1. Для df=6 та α=0,05 χ2*=12,59
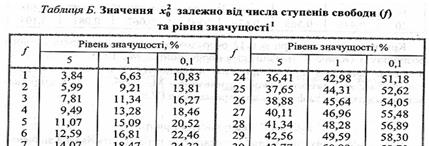
3.2. χ2=31,85 > χ2*=12,59
3.3. Гіпотезу-0 про те, що змінні є незалежні одна від одної відхиляємо і приймаємо Гіпотезу-1, що змінні є залежні одна від одної.
3.4. Підставою для відхиляння Гіпотези-0 є також й інший показник: Asymptomatic Significance (2-sided). Пригадаймо, що це є q – ймовірність помилки першого роду (типу альфа), тобто ймовірність допуститися помилки, відкидаючи Гіпотезу-0 як фальшиву, в той час коли вона є коректною.
В рамках тесту χ2 співвідношення між значеннями q та силою залежності числових (відсоткових) розподілів показникової змінної від категорій факторної змінної виглядає наступним чином:

| Інтервали | Ймовірність помилки (q) | ДІЯ: | Оцінка залежності змінних | |
| формулювання | символ | |||
| 0.00 ≤ q < 0.01 | Ймовірність помилки при відхилянні Гіпотези-0 є дуже малою (значимою на рівні 0.01) | відкидаємо Гіпотезу 0 | NN(%%) розподіли показни-кової змінної є дуже залежні від категорій факторної змінної (залежність є значимою на рівні 0.01) | ** |
| 0.01 ≤ q < 0.05 | Ймовірність помилки при відхилянні Гіпотези-0 є малою (значимою на рівні 0.05) | NN(%%) розподіли показни-кової змінної є залежні від категорій факторної змінної (залежність значимою на рівні 0.05) | * | |
| 0.05 ≤ q ≤ 1.00 | Ймовірність помилки при відхилянні Гіпотези-0 є великою | приймаємо Гіпотезу 0 | NN(%%) розподіли показни-кової змінної є не залежні від категорій факторної змінної | ns |
q=0,000 < 0,01, а тому ймовірність помилки є дуже малою.
Отже, числові (відсоткові) розподіли показникової змінної є дуже залежні від категорій факторної змінної (залежність є значимою на рівні 0,01).
4. Загальний висновок: “Ставлення респондентів до посилення в країні контролю за виконанням трудової дисципліни, включаючи перевірку громадян на вулицях у робочий час, дуже сильно залежить від рівня їхньої освіти.”
5. Деталізований висновок в рамках загального висновку здійснюємо за аналізом відсоткових розподілів у Таблиці кростабуляцій, а також за різницями (Residuals) між відповідними спостережуваними та очікуваними частотами.

Дата добавления: 2015-10-28; просмотров: 111 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тест хі-квадрат (χ2) для встановлення міри зв’язку між двома дискретними змінними (тест χ2 незалежності). | | | о лишении родительских прав |