
Читайте также:
|
Ви вже знаєте, що тест хі-квадрат (χ2) базується на обчисленні різниці між так званими “очікуваними” значеннями та значеннями, що спостерігаються.
У випадку встановлення міри зв’язку між двома змінними схематичний формат тесту виглядає наступним чином.
Очікуваний розподіл значень: у відповідності до встановлених правил ми очікуємо, що кореляції немає (ідеальний, змодельований стан). В такому випадку, якщо розділити поле графіку на чотири однакових сегменти, тоді в кожному з них є по 25% всіх значень.
В реальності кореляція завжди є, навіть якщо й дуже мала. В реальності, якщо розподілити поле графіку на чотири однакових сегменти, то в кожному з них є різні відсотки значень, наприклад, 10%, 35%, 5%, 50%.
Порівнюючи два графіки бачимо, що чим більшою є різниця між очікуваними значеннями та тими, що спостерігаються, тим сильнішою є кореляція між змінними. 1900 року Карл Пірсон запропонував наступну формулу для обчислення хі-квадрату:
 , де fe – частоти, що очікуються (expected); fo – частоти, що спостерігаються (observed).
, де fe – частоти, що очікуються (expected); fo – частоти, що спостерігаються (observed).
ПРИКЛАД
Уявімо, що Ви прагнете встановити, чи рівень агресивності людей на роботі залежить від кількості ситуацій, коли вони переживали страх. Отже, маємо дві змінні: А – чи більшість часу на роботі проходить в умовах високого, середнього чи низького рівня страху – це ви з’ясовували у самих робітників; Б – рівень агресивності робітників (низький, високий) – його ви з’ясували у тих, хто керує їхньою роботою. Ви дослідили ситуацію зі 100 робітниками певного підприємства. Результати досліджень представлено в таблиці:
Таблиця №1. Спостережувані частоти.
| Змінна Б | Змінна А Кількість робітників з рівнем страху: | ЗАГАЛОМ | |||
| низький | середній | високий | |||
| N робітників з рівнем агре-сивності: | високий | 4 (10) | 18 (25) | 18 (15) | 40 (50) |
| низький | 16 (10) | 32 (25) | 12 (15) | 60 (50) | |
| ЗАГАЛОМ |
Це є так звана таблиця контингентності.
Отже, дослідницьке запитання: “Чи рівень агресивності людей на роботі залежить від кількості ситуацій, коли вони переживали той чи інший рівень страху?” Іншими словами: “Чи кількість спостережуваних частот в межах однієї змінної залежить від кількості спостережуваних частот в межах іншої змінної?”
Нагадаймо, що це є тест χ2 незалежності змінних одна від одної. Це означає, що при проведенні зазначеного тесту Гіпотеза-0 має наступний універсальний зміст: “Дві змінні є незалежними одна від одної.” Таким чином, якби значення змінної Б не залежали від значень змінної А, то в кожній з колонок, наприклад, були б однакові числа (вони є представлені в дужках).
Отже, ми маємо спостережувані частоти. Щоб мати можливість застосувати формулу Пірсона для обчислення хі-квадрату нам потрібні очікувані частоти. В рамках таблиці контингентності очікувані частоти обчислюються у відповідності до наступних двох основних умов:
- очікується, що змінні є незалежними одна від одної;
- очікувані частоти розраховуються із врахуванням, що факторною змінною може бути або одна, або друга.
За таких умов для кожної з комірок таблиці контингентності ви розраховуєте ймовірність одночасності двох відповідних подій. Наприклад, якою є ймовірність одночасності як високої агресивності, так і низького рівня страху (в таблиці це є зелена комірка).
| ймовірність “високої агресії” та “низького страху” | = | ймовірність “високої агресії” | Х | ймовірність “низького страху” |
| ймовірність “високої агресії” | = | загальна кількість осіб з високою агресією | : | загальна кількість осіб у вибірці | 40 |
| ймовірність “низького страху” | = | загальна кількість осіб з низьким страхом | : | загальна кількість осіб у вибірці | 20 |
| ймовірність “високої агресії” та “низького страху” | = | 40 | Х | 20 |
| очікувана частота в зеленій комірці | = | ймовірність одночасності двох відповідних подій | х | загальна кількість осіб у вибірці | 
| 
|
| Очікувана частота у певній комірці | = | Е | = | (R)(C) N |
де: R – загальна кількість одиниць спостереження у відповідному рядку;
C – загальна кількість одиниць спостереження у відповідній колонці;
N – загальна кількість одиниць спостереження.
За даними Таблиці №1 студенти розраховують відповідні очікувані частоти у відповідних комірках.
Таблиця №2. Очікувані частоти.
| Змінна Б | Змінна А Кількість робітників з рівнем страху: | |||
| низький | середній | високий | ||
| N робітників з рівнем агре-сивності: | високий | 
| 
| 
|
| низький | 
| 
| 
|
Перевірка: загальна кількість очікуваних частот має відповідати загальній кількості спостережуваних частот: 8+20+12+12+30+18=100.
Ви також знаєте, що для проведення тесту хі-квадрат необхідно обчислити df – ступінь свободи.
 ,
,
де: KR – кількість категорій змінної, що займає рядки
KC – кількість категорій змінної, що займає колонки.
Для нашого прикладу:

Процедура тесту χ2
1. Гіпотеза-0. Агресивність та відчуття страху є незалежними одна від одної змінними (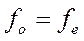 )
)
2. Гіпотеза-1. Агресивність та відчуття страху є залежними одна від одної змінними ( )
)
3. Для α=0,05, та для df=2 за даними таблиці знаходимо χ2*= 5,99

3. Створюємо таблиці спостережуваних та очікуваних частот.
4. Обчислюємо χ2

5. Оскільки 8,67 > 5,99, то Гіпотезу-0 відхиляємо.
Робимо висновок: Рівень агресивності людей на роботі залежить від кількості ситуацій, коли вони переживали страх.
Дата добавления: 2015-10-28; просмотров: 423 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Remember the pronunciation of the following geographical names. | | | Тест χ2 з використанням програмного забезпечення SPSS |