равноточных наблюдений при прямых измерениях.

Лабораторная работа №4

Обработка результатов многократных

равноточных наблюдений при прямых измерениях.

Цель работы: изучить порядок обработки результатов многократных наблюдений при прямых измерениях; приобрести навыки стандартной обработки результатов наблюдений, оценки погрешностей и предоставления результатов измерений.

1. Теоретические сведения

В измерительной практике для уменьшения влияния случайных погрешностей на результат измерения проводят измерения с многоразовыми наблюдениями, а затем статистически обрабатывают полученные результаты. При этом могут быть использованы различные процедуры обработки.

Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях.

Результат измерения содержит погрешность, представляющую сумму систематической составляющей D_С и случайной составляющей :

.

Эти две составляющие погрешности резко отличаются по своим свойствам.
Их анализ, способы оценки и уменьшение совершенно различны.

Систематическая погрешность D_С остается постоянной или изменяется по определенному закону при повторных измерениях одной и той же физической величины. Она является математическим ожиданием погрешности измерения

.

Обнаружение систематической погрешности – трудоемкая операция и может быть выполнена несколькими способами:

1) Проверка данного измерительного прибора с помощью образцового (более точного). При одновременном измерении одной и той же физической величины получают разные показания X _раб и X _обр. Их разность

является абсолютной систематической погрешностью прибора.
Тогда в показания рабочего прибора вводится поправка П, равная

При этом за результат измерения необходимо принимать величину

.

2) Метод замещения. В этом случае измеряемая величина 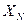заменятся известной величиной таким образом, чтобы показания прибора осталось неизменными. Тогда результат измерения .

3) Метод компенсации по знаку применяется при направленном действии причины, вызывающей систематическую погрешность. Выполняют измерения так, чтобы погрешность входила с разными знаками в формулы

; ,

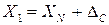тогда .

Переменные систематические погрешности разделяют на прогрессирующие и периодические. Для устранения этих составляющих необходимо найти функциональную связь погрешности и влияющего фактора и вводить поправку на основании полученных зависимостей и таблиц.

Сложную задачу по выявлению и исключению систематической погрешности не всегда удается довести до конца и поэтому остается неисключенная часть систематической погрешности.

Нетрудно убедиться, что результат измерения – случайная величина.
Для этого достаточно измерить несколько раз одну и ту же физическую величину с помощью прибора, обладающего достаточно высокой чувствительностью. Результаты измерений будут в общем случае отличаться друг от друга. Это объясняется влиянием многих дестабилизирующих факторов, к которым можно отнести: тепловой шум, шум электронных приборов, случайные воздействия на результат измерения коммутационных процессов в цепях, случайное изменение электромагнитных полей, температуры окружающей среды, влажности, вибрации, напряжения питания измерительного прибора и т.д. Полное совпадение результатов измерений всегда указывает на то, что чувствительность средств измерений недостаточна для того, чтобы обнаружить это явление.

Таким образом, случайная погрешность изменяется нерегулярно, непредсказуемо при повторных измерениях. Она вызывается большим количеством причин, характер и размер влияния которых на измеряемую величину при единичном измерении не может быть определен. Однако путем выполнения многократных наблюдений и путем обработки результатов наблюдений статистическими методами можно дать оценку этим погрешностям. Вклад в случайную погрешность вносит случайная составляющая погрешности средства измерений.

Одной из важнейших характеристик случайной погрешности является закон распределения плотности вероятности – плотность распределения вероятностей или – функция распределения вероятностей.

Законы распределения могут быть дискретными (для дискретных случайных величин) и непрерывными (для непрерывных величин).

Дискретный закон распределения представляет совокупность значений случайной величины и соответствующих им вероятностей , причем (условие нормировки закона распределения вероятностей дискретной случайной величины).

Для непрерывных случайных величин с известным законом распределения вероятность того, что данная случайная величина (рис. 4.1) примет значение в интервале от до , определяется площадью, ограниченной этой кривой и осью абсцисс, т.е.

.

Рис. 4.1. Нормальный закон распределения.

Следует помнить, что 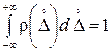является условием нормировки для непрерывной случайной величины.

Если дестабилизирующих факторов, обуславливающих случайную погрешность много (3 и более), то закон распределения плотности вероятности будет стремиться к гауссовой кривой – нормальному закону распределения (рис. 4.2, а)

,

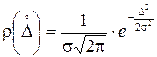если считать, что исключена систематическая погрешность и М[D] = 0, т.е. .

а) б)

Рис. 4.2. Кривые Гаусса а) для разных значений среднеквадратического отклонения s, б) для разных значений систематической составляющей погрешности.

Если в составе погрешности есть систематическая погрешность, то закон распределения плотности вероятности будет смещен на величину .

Характер закона распределения изменяется в зависимости от параметров s и s² (рис. 4.2, а). Дисперсия характеризует рассеяние случайной величины относительно среднего значения. Среднеквадратическое значения отклонения (СКО) . Дисперсия и СКО характеризуют точность измерений. Чем больше s² и s, тем меньше точность, т.е. больше погрешность.

При нормальном законе распределения вероятность появления случайной погрешности в интервале от –D_гр до +D_гр определяется выражением

.

При введении нормированной случайной переменной выражение P (D) преобразуется к виду:

,

где Ф(z) – интеграл вероятности.

Доверительная вероятность P _дов при заданных граничных значениях погрешности – это вероятность нахождения случайной величины внутри доверительного интервала D_дов (доверительных границ). Доверительная вероятность определяется площадью под кривой (на рис. 4.3 заштрихованная область).

Рис. 4.3.

Функция Ф(z) табулирована или определяется по графику (рис. 4.4).

Рис. 4.4. Функция Лапласа для разных значений z _гр.

Если задана P _дов, то по графику или таблице находят z _гр, затем определяют D_гр = z _гр×s. Доверительный интервал D_дов = –D_гр … +D_гр, он с заданной вероятностью накрывает истинное значение , Р _дов = …

В зависимости от целей измерений доверительную вероятность на практике устанавливают Р _дов = 0,95 … 0,99.

За максимальное значение погрешности D_max принимают D_max = ±3s, что соответствует вероятности появления погрешности в этом интервале Р _дов = 0,9973. Вероятность того, что погрешность превысит максимальное значение определяется выражением . Это означает, что погрешность в 369 случаях из 370 попадает в интервал ±3s и лишь в одном случае выходит за эти пределы.

Информационная концентрация измерений

С точки зрения измерительной информации суть измерений состоит в сужении интервала неопределенности измеряемой величины от значения, известного до проведения измерения, до проведения измерения, до некоторой величины d, которая стала известной после проведения измерений.

Мерой неопределенности знаний о значении измеряемой величины является энтропия:

Энтропия является единственной числовой характеристикой закона распределения величины x.

Разность энтропий до и после измерения физической величины есть количество информации:

,

где Н (x) – априорная энтропия (до измерения);

Н (x / x_N) – апостериорная энтропия (после измерения).

Энтропия погрешности или дезинформирующее

действие погрешности

Основное преимущество информационного подхода к описанию измерений состоит в том, что размер энтропийного интервала неопределенности d можно найти строго математически для любого закона распределения. Это исключает недоразумение при произвольном выборе различных значений доверительной вероятности.

Найдем энтропию погрешностей основных законов распределения.

1. Энтропия погрешности с равномерным законом распределения плотности вероятности.

Максимальное значение погрешности равномерного закона распределения принимают за энтропийное значение D _m = D_Э. Соотношение между энтропийным D_Э и среднеквадратическим s значениями погрешности характеризуют энтропийным коэффициентом: Тогда

а поскольку для равномерного закона то

Энтропийный интервал погрешностей

2. Энтропия погрешности с нормальным законом распределения плотности вероятности.

Энтропийный коэффициент равен а энтропийный интервал

Энтропийное значение погрешности,

представленное гистограммой распределения

Если на основе ограниченного числа измерений была построена ступенчатая гистограмма, то, найдя ее энтропию, можно затем заменить гистограмму законом распределения выбранной формы (равномерным, нормальным) и определить энтропийный интервал погрешности.

Пусть гистограмма состоит из m столбов.

Высота столбца: , где j = 1, 2, …, m – количество интервалов; n –число всех измерений; ni – число измерений, попавших в j -й интервал.

Энтропия погрешности определяется суммой энтропийных значений каждого j -го интервала:

2. Порядок выполнения работы

1. Измерить сопротивление n резисторов одного номинала прибором Щ 4313 в режиме омметра. Результаты наблюдений занести в табл. 4.1.

2. Предполагаем, что измеряемые значений R_i подчиняются нормальному закону распределения. Последовательность обработки результатов проводить в соответствии с методикой, изложенной в ГОСТ 8.207–76:

2.1. Вычислить среднее арифметическое значение измеряемой величины

2.2. Вычислить разности между результатами отдельных наблюдений R_i и среднего значения – случайное отклонение результата наблюдения . Значение D _i занести в табл. 4.1. Определить сумму всех погрешностей .

При большом числе измерений сумма случайных погрешностей стремится к нулю . Этот вывод основывается на аксиоме случайности теории случайных погрешностей, что при очень большом числе измерений и при отсутствии систематических D_С погрешностей, положительные и отрицательные погрешности встречаются одинаково часто.

2.3. Рассчитать величины квадрата абсолютной погрешности , результаты занести в табл. 4.1.

Таблица 4.1

№	Измеренное значение Ri, Ом, кОм, МОм	Абсолютная погреш-ность измерения	Квадрат абсолютной погрешности
…	…	…	…
n
	Среднее арифметическое значение сопротивлений	Сумма абсолютных погрешностей	Сумма квадратов абсолют-ных погрешностей

Сумма квадратов случайных погрешностей должна быть минимальной . Такой вывод основывается на аксиоме распределения, что при большом количестве измерений малые погрешности встречаются чаще, чем большие; очень большие погрешности практически не встречаются.

2.4. Определить оценку среднеквадратического отклонения результатов каждого из n одноразовых наблюдений .

2.5. Исключить аномальные результаты (грубые промахи) по критерию «трех сигм». Для этого из ряда значений D _i найти наибольшие и сравнить их с . Такой критерий надежный при числе измерений . Если , то подозреваемый в аномальности результат D_max исключить, а затем повторить сначала расчеты по пунктам 2.1. – 2.4.

2.6. Найти оценку СКО среднего арифметического значения .

2.7. Определить доверительные границы случайной составляющей погрешности и записать результат измерений. Если за результат измерений принято среднее значение , то

При Р _дов = 0,997 z _гр = 3 и .

При любой другой доверительной вероятности Р _дов можно воспользоваться табличным (или из графика) значением интервала вероятности Ф(z) = Р _дов, по его значению можно найти z _гр и далее, так как , можно определить D_гр и записать результат

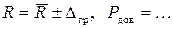
2.8. В случае, если число измерений n мало , то ,
где t – коэффициент Стьюдента, который определяют из табличных данных при заданных Р _дов и количестве (n) наблюдений.

2.9. Учитывая, что систематическая погрешность D_С вошла в состав результата измерений , необходимо определить вычислить доверительные границы неисключенной систематической погрешности. В качестве D_С используют погрешность средства измерения

,

где g – класс точности прибора, %.

Для прибора Щ 4313 относительная погрешность определяется по формуле:

,

где a и b – коэффициенты, зависящие от конечного значения шкалы R _к.

При R _к = 500 Ом, a = b = 1,5. При R _к = 5 кОм и более, a = b = 0,5.

Абсолютная погрешность: .

В случае, если , то неисключенной систематической погрешностью пренебрегают и принимают D = D_гр; если , то пренебрегают случайной погрешностью и считают, что D = D_С. В случае равенства вычисляют 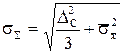, , и тогда , а результат представляют в виде:

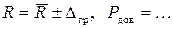
Числовое значение результата измерения должно заканчиваться цифрой того же порядка, что и значение погрешности D. При этом число значащих цифр при определении D не должно превышать двух.

3. Определить закон распределения погрешностей результатов измерений.

Для идентификации закона распределения необходимо построить гистограмму (рис. 4.4). Для этого весь диапазон D _i разбивают на m одинаковых интервалов. Значение m должно быть нечетным (m = 9 … 13).

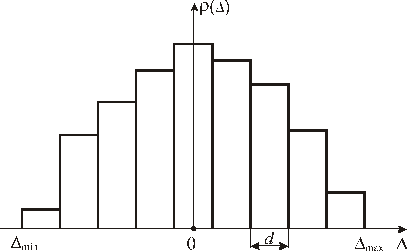
Рис. 4.4. Гистограмма.

Ширину интервала определяют по соотношению:

,

где D_max, D_min – соответственно наибольшее и наименьшее значение погрешности D _i; m – количество интервалов.

Затем подсчитывают вероятность нахождения случайной погрешности в j интервале

,

где j – 1, 2, …, m; n_j – число погрешностей, которые попадают в j -ый интервал;

n – число всех измерений.

Если погрешность попадает на границу интервала D _j, то ее можно отнести либо к j -му интервалу, либо к (j +1)-му интервалу, т.е. она учитывается только один раз.

По оси результатов наблюдений откладывают интервалы D _j в порядке нарастания номеров и на каждом интервале строится прямоугольник высотой (средняя плотность в интервале D _j = d).

В этом случае площадь под гистограммой будет равна единице. Полученную гистограмму аппроксимируют кривой и делают выводы о законе распределения.

Как способ оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения используется критерий согласия. Наибольшее распространение в практике получил критерий Пирсона.

3.1. Приравняв энтропию распределения, представленного гистограммой, к энтропии равномерного закона, получим энтропийное значение случайной погрешности D_Э. При этом равенство энтропий Н _гист(D) = Н _равн(D) создает одинаковое дезинформирующее действие погрешности на измеряемую величину.

Н _гист(D) = Н _равн(D) = ln(2D_Э).

Þ

С учетом полученного значения D_Э результат измерения сопротивления R запишем в виде:

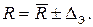
3.2. Приравняем энтропию распределения, представленного гистограммой, к энтропии нормального закона:

Вычислим s:

Энтропийный интервал: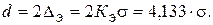

Используя рассчитанное значение s, можно построить график r(D) нормального закона распределения по известной формуле .

Þ

Площадь под кривой r(D) и площадь всех столбцов гистограммы должны быть одинаковыми. Для наглядности сравнения кривую r(D) нормального закона распределения необходимо совместить с рисунком гистограммы (см. рис.).

Дата добавления: 2015-10-23