Указатели см таблицу 3. Операции, проводимые над математическими моделями

Читайте также:

ТЕКСТ???

Билет 5

Операции, проводимые над математическими моделями

1. Анализ (прямая задача) – вычисление характеристик по известным значениям параметров. На любом уровне различают одновариантный анализ, когда анализируется ОС однозначно заданным параметрам, и многовариантный анализ, когда определяются характеристики при изменении конструкционных параметров.

Анализ по своей сути представляет моделирование работы проектируемого на данном уровне объекта с целью определения его характеристик. В большинстве случаев анализ реализуется в настоящее время как математическое, компьютерное моделирование. В некоторых случаях применяется макетирование (изготовление проектируемого объекта).

Характерной особенностью анализа является наличие нескольких (иногда довольно большого) числа уровней, отличающихся глубиной и полнотой анализа и его трудоемкостью. На начальных уровнях определяется сравнительно небольшое количество основных характеристик. Это требует минимального количества вычислений. Поэтому эти уровни характеризуются малой трудоемкостью. На следующих, более глубоких уровнях, анализируется намного большее число характеристик. Это требует возрастающего объема вычислений, причем трудоемкость различных уровней анализа может отличаться в десятки и даже сотни раз. Разделение анализа на уровни очень важно для экономии ресурсов компьютера, времени проектировщика и исключения ненужных затрат. На каждом уровне проектирования можно выделить следующие виды анализа: одновариантпый (точечный), поливариантпый, технологический.

Одновариантным называется анализ, при котором характеристики проектируемого объекта определяются только для одного набора значений параметров. Он применяется в случае, когда требуются значения характеристик конкретного проектного решения. На практике он распространен наиболее широко. На языке математики об одновариантном анализе можно сказать, что при его реализации вычисления производятся в одной точке пространства параметров. Поэтому такой вид анализа называют также точечным.

Поливариантным называется анализ, при котором характеристики проектируемого объекта определяются для нескольких вариантов. Последние имеют по отношению друг к другу небольшие отличия: возмущения или приращения в значениях некоторых параметров. Тем самым как бы определяется чувствительность характеристик объекта к изменениям параметров. Поэтому поливариантный анализ называют иногда анализом влияния параметров или анализом чувствительности. При полном анализе чувствительности определяется влияние всех параметров на все характеристики.

2. Синтез (обратная задача) – первоначальное формирование конструктивных параметров для получения заданного значения функции. В основном, это эвристическая операция.

Задача синтеза заключается в создании первоначального описания объекта проектирования по техническому заданию (на данном уровне данной ветви). Формально она сводится к определению неизвестного вектора параметров x по заданному вектору характеристик f.

Задача синтеза отличается крайней эвристичностью. Особенно это относится к структурному синтезу. Задача синтеза обладает также явно выраженной объектной ориентированностью, поскольку бесспорно, что методы синтеза не только оптических или электронных схем, но даже разных оптических схем, совершенно различны. Из-за высокой степени эвристичности синтез (особенно структурный) в значительной своей части выполняется непосредственно проектировщиком. Тем более, что для опытного проектировщика синтез путем правильного выбора из типовых структур с возможной их модификацией является сравнительно нетрудоемкой, хотя и эвристической задачей. Синтез принципиально новой, ранее неизвестной

структуры является весьма редким и относится к числу трудных изобретательских задач, выполняемых лишь опытными, талантливыми

проектировщиками. Различают два этапа синтеза – структурный и параметрический. На первом

этапе определяется структура проектируемого объекта, то есть количество и типы элементов, последовательность расположения и связи между ними; на втором – определяются численные значения параметров этой структуры. Так, при структурном синтезе оптических систем определяют из скольких линз будет состоять проектируемый объектив.

После структурного синтеза следует параметрический, в процессе

которого определяются численные значения параметров синтезированной

структуры.

3. Оптимизация – направленное изменение конструктивных параметров с целью достижения полученных значений характеристик. Операция оптимизации является совершенно объектно-вариантной и детерминированной. Выбор оптимизационной модели – чисто эвристическая операция.

Последней и, вероятно, наиболее важной задачей проектирования является оптимизация. Она представляет собой плавное, постепенное изменение параметров проекта с целью улучшения его качества, достижения оптимальных наиболее благоприятных, наилучших значений заданных характеристик. Оптимизация не может начинаться “от нуля”, от пустого места, для нее необходимо начальное приближение, стартовая точка. Эта точка соответствует предварительно синтезированной структуре, полученной с некоторыми приближенными, начальными значениями параметров. По завершении оптимизации определяют окончательные значения параметров, обеспечивающие лучшие, оптимальные значения характеристик.

Существенно, что при оптимизации структура проектируемого объекта остается неизменной, меняются лишь значения параметров этой структуры. В количественном выражении эти изменения часто столь малы, что оптимизированные конструкция или схема внешне практически не отличаются от исходных, хотя улучшение характеристик может быть разительным. Проблема оптимизации состоит в том, чтобы найти правильную

закономерность одновременного изменения большого количества параметров, или, другими словами, найти нужную “траекторию движения” в пространстве параметров. Для решения этой проблемы привлекается довольно сложный математический аппарат.

Для выполнения оптимизации необходимо прежде всего построить так называемую оптимизационную модель объекта. Эта модель включает в себя параметры оптимизации, оптимизируемые функции, критерий оптимизации, а также ограничения.

Параметры оптимизации – это те параметры, изменением которых пытаются добиться улучшения характеристик. Обычно не все параметры структуры объекта (конструктивные параметры) включаются в оптимизацию. Так как при прочих равных условиях, трудоемкость оптимизации пропорциональна числу параметров, то начинать оптимизацию надо с небольшого количества тщательно отобранных параметров, а затем их количество постепенно увеличивается. По этой же причине при оптимизации часто изменяют не непосредственно конструктивные параметры, а другие величины, связанные с ними определенным образом.

Критерий оптимизации, или оценочная функция, – это число, дающее общую оценку оптимизации по всем функциям. Обычно в качестве критерия выбирают сумму квадратов оптимизируемых функций. Правильный выбор оптимизируемых функций является одним из ключевых моментов оптимизации. Этот выбор должен удовлетворять трем противоречивым требованиям: адекватности, простоты и низкой трудоемкости.

Трудоемкость оптимизации определяется тем количеством вычислений, которые необходимых для реализации процесса нахождения значений функций по текущим значениям параметров. Этот процесс (часто называемый “пробой”) при оптимизации повторяется гигантское количество раз. Поэтому затраты на оптимизацию прямо пропорциональны трудоемкости “пробы” и, если она оказывается большой, то процесс оптимизации может стать долгим, а

олучение результатов за обозримое время проблематичным.

Марки аберраций сагиттального сечения

┌─────┬───────┬───────────────────────────────────────┐

│ имя │указа- │ аберрация │

│ │тели │ │

├─────┼───────┼───────────────────────────────────────┤

│ DYS │ LJI │ мер.составляющая аберрации саг.сечения│

│ DXS │ LJI │ саг.составляющая аберрации саг.сечения│

└─────┴───────┴───────────────────────────────────────┘

Указатели см таблицу 3

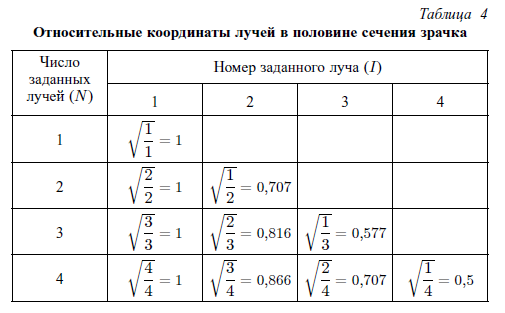
По умолчанию через систему рассчитывается только один луч, идущий через правый край входного зрачка. Другое число лучей задается идентификатором RAYS = N;, где N может принимать значения от 1 до 4. Задание разбиения зрачка через произвольные относительные величины осуществляется с помощью идентификатора PCS(*) = 1,...;

В правой части выражений через запятую указывают необходимые относительные координаты лучей по зрачку, например:

RAYS = 4; PCS(*) = 1, 0.8, 0.5, 0.3;

Билет 7

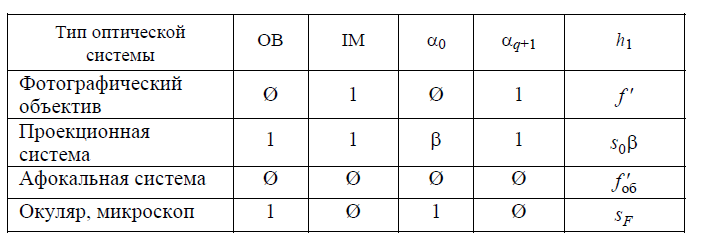
Характеристики предмета и изображения для системы OB=0, IM=1

Фотообъектив

α₀=0, α_n’=1, h’=f’_об

Предмет задаётся в угловой мере

Изображение задаётся в линейной мере

Обобщенное увеличение задаётся передним фокусным расстоянием (мм)

Оптимизационная модель телескопа

Пусть дан телескоп Кеплера, с симметричным окуляром, в телескопах по той причине что поле не велико правят сферическую аберрацию, кому и хроматизм положения.

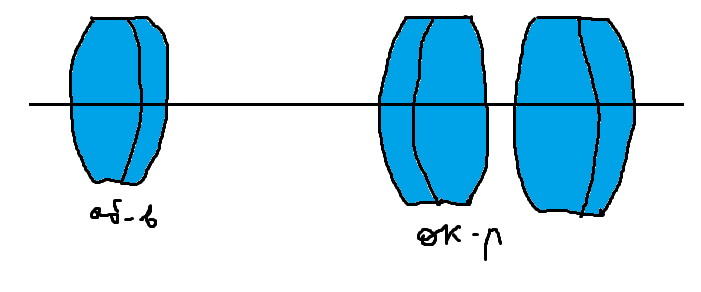
Поскольку окуляр обычно не трогаем то правим кривизны объектива и расстояние между объективом и окуляром, но необходимо чтобы система оставалась афокальной и при этом видимое увеличение не изменялось.

PAR(*)=C/1-3,D/3;

EQF(*)=VG0,SG’;

MF(*)=DSA/’0,DYA/01,DYM/011*;

Билет 8

Описание поверхности предмета и изображения и величины поля для случая OB=1, IM=0

Микроскоп

α₀=1, α_n’=0, h’=…

Предмет задаётся в линейной мере

Изображение задаётся в угловой мере

Обобщенное увеличение задаётся 1/f’ (1/мм)

Оптимизационная модель телескопа

PAR(*)=C/1-3,D/3;

EQF(*)=VG0,SG’;

MF(*)=DSA/’0,DYA/01,DYM/011*;

Билет 9

Задание апертуры для различных типов ОС

Количество световой энергии, проходящей через оптический прибор для осевой точки предмета основной длины волны, может ограничиваться апертурной диафрагмой и оправами оптических компонентов. Выходной зрачок задается как апертурная диафрагма, расположенная за оптической системой. Следует иметь в виду, что апертурная диафрагма (материальный экран с отверстием) в центрированных оптических системах всегда перпендикулярна оптической оси прибора, а входной зрачок всегда перпендикулярен главному лучу, т. е. разворачивается относительно оптической оси для своей точки предмета, что позволяет рассчитывать оптические системы с большими угловыми полями.

Если задана апертурная диафрагма, то ее местоположение определяется числом поверхностей до диафрагмы ND и расстоянием SD от предыдущей поверхности в миллиметрах, а проходящая энергия ограничивается высотой y_D на апертурной диафрагме. В случае, когда SD=Ø, апертурная диафрагма принимает форму той поверхности, с которой она совпадает. Если апертурная диафрагма расположена перед оптической системой, то ND=Ø, а SD – расстояние от первой поверхности до апертурной диафрагмы.

Передняя и задняя апертуры воспринимаются по-разному в зависимости от того, где расположен предмет (изображение). Для систем удаленного типа под апертурой понимается произведение половины входного (выходного) зрачка на показатель преломления среды в пространстве предметов (изображения): Α = n ₀ h _вх.зр(Α′ = n ′ h _вых.зр). Положение входного (выходного) зрачка задается расстоянием SP (SP′) в миллиметрах от первой (последней) поверхности.

Для систем ближнего типа положение входного (выходного) зрачка задается в диоптриях как расстояние SP (SP′) относительно поверхности предмета (изображения). Передняя (задняя) апертура является произведением синуса апертурного угла в пространстве предметов (изображения) на показатель преломления среды в этом пространстве: Α = n ₀sinσ₀ (Α′= n_i sinσ _i).

Какие операции необходимо осуществить, чтобы, ставя в телескопическую систему призму (плоско-параллельную пластинку), получить афокальную систему.

Есть ТС, вставляются две поверхности (F2-перестройка-вставить поверхность) между окуляром и объективом, материал К8, расстояние от второй поверхности до окуляра равно -D₅= 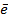+S_F_,где 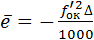, переднее расстояние подгоняем (F2-система-подгонка характеристик-положение пл. Гаусса-осевое расстояние-и вписываем номер поверхности расстояние которой мы меняем, в данном случае третья)

Удлинение призмы в зависимости от показателя преломления н * длинну

Билет 10

Задание оптических поверхностей

Программа Opal позволяет задавать оптические системы через радиусы, кривизны и углы первого вспомогательного луча. Перед заданием оптической поверхности необходимо настроить программу на данный вид задания поверхностей. Если в системе присутствуют асферические поверхности, то оптическую систему необходимо описывать через радиусы.

Оптические поверхности в OPAL-PC рассматриваются как глад-

кие непрерывные поверхности, преломляющие или отражающие лучи.

Поверхности типа линз Френеля не рассматриваются.

Поверхности описываются уравнением относительно координат

X, Y, Z точки на поверхности. Общий вид уравнения

f(x,y,x) = 0 (2.1)

Возможны следующие поверхности: плоскость, сфера, несфери-

ческие поверхности вращения второго и высшего порядков, цилинд-

ры, торы, конусы, поверхности с дополнительными деформациями.

Входной зрачок. Апертурная диафрагма. Примеры задания для различных ОС.

Если ND=999, то это значит, что в системе задан входной зрачок, а не диафрагма и SD задает положение входного зрачка. При OB=0, SD есть расстояние в мм от первой поверхности до зрачка, при OB=1 в диоптриях.

Пример: допустим предмет дальнего типа входной зрачок расположен на 15мм перед ОС, и имеет высоту 10мм, его задается след. образом: ND=0, SD=-15, А=10

Пример2: допустим система ближнего типа АД расположен после 2-й поверхности системы на расстоянии 5мм, и синус апертурного угла равен 0.5, его задается след. образом: ND=2, SD=10, передняя апертура А=0.5 sin

Билет 11

Оценочные функции и критерии качества при оптимизации.

При выполнении процесса оптимизации необходимо:

1. Определить критерий качества

2. Задать параметры, которые могут быть изменятся

3. Задать ограничения на те параметры и функции, которые изменяются

Под исправляющей функцией будем понимать те величины, которые при оптимизации должны получить определённые значения => каждая текущая аберрация вычисляется из заданной величины, делится на норму и умножается на весовой коэффициент. Отмасштабированная функция называется исправляющей. Сумма квадратов исправляющей функции является критерием качества, т.е. при оптимизации минимальному критерию качества. Чем меньше величина критерия качества при заданном количестве функций, тем оптимальней решение.

ключевых моментов оптимизации. Этот выбор должен удовлетворять трем противоречивым требованиям: адекватности, простоты и низкой трудоемкости. Требование адекватности означает, что минимизация суммы квадратов оптимизируемых функций должна соответствовать действительному улучшению качества проектируемого объекта. Сложность обеспечения адекватности заключается в том, что, во-первых, истинное качество проекта часто описывается достаточно большим набором характеристик, иногда сформулированных недостаточно четко, и поэтому часто не позволяющим количественно описать это качество суммой квадратов функций. Во-вторых, в тех случаях, когда это можно сделать, оптимизируемые функции получаются сложными и не удовлетворяют требованиям простоты и низкой трудоемкости. Требование простоты оптимизации математически выражается линейным характером зависимости оптимизируемых функций от параметров. Чем ближе указанные зависимости к линейным, тем успешнее идет оптимизация. При строгой линейности современные методы дают решение за один шаг. Напротив, чем более нелинейны эти функции, тем больше шагов требует процесс оптимизации, тем медленнее он сходится.

Задание предела изменения коррекционных параметров. Примеры.

С помощью ограничений можно описать интервал изменения коррекционных параметров. Минимальное значение (ограничение слева) коррекционного параметра обозначается знаком «<», а максимальное (ограничение справа) — знаком «>». Идентификатор состоит из указателя, вида марки коррекционного параметра, его ограничения, номера параметров (в скобках), после знака равенства указываются предельные значения для каждого параметра, указанного в скобках.

Пример:

D < (1 − 3) = 2, 3, 4;

D > (1 − 3) = 10, 5, 7;

Данная запись означает, что первая толщина (расстояние от вершины первой до вершины второй поверхности вдоль оптической оси) изменяется от 2 до 10 мм, вторая толщина изменяется от

3 до 5 мм и т. д.

Билет 12

Параметры оптимизации и связи между ними.

В процессе оптимизации между конструктивными параметрами могут быть

выдержаны определенные связи вида:

пз = кс * пс

пз, пс - значения связанного(зависимого) и свободного (независимого) параметров соответственно; кс - коэффициент связи.

Связи выдерживаются для следующих пар параметров:

радиус - радиус;

радиус - толщина;

толщина - положение диафрагмы;

передний отрезок - задний отрезок;

передний отрезок - радиус первой поверхности;

задний отрезок - радиус последней поверхности.

Описание связей включает:

список марок свободных параметров;

список марок связанных параметров;

список коэффициентов связей (массив чисел).

Марки свободных параметров определяются оператором:

PARF(*) = пс1,пс2,...,псn;

или

PARF(к1-к2) = пск1,...,пск2;

или

PARF(к1,к2) = пск1,пск2;

где n - общее число марок свободных параметров;

пс1,пс2,пск1,пск2,псn - марки свободных параметров

Марки связанных параметров указываются в строгом соответствии с расположением соответствующих им марок свободных параметров с помощью оператора:

PARC(*) = пз1,пз2,...,пзn;

или

PARC(к1-к2) = пзк1,...,пзк2;

или

PARC(к1,к2) = пзк1,пзк2;

где n - общее число марок связанных параметров;

пз1,пз2,пзк1,пзк2,пзn - марки связанных параметров

Коэффициенты связи записываются в строгом соответствии с расположением марок свободных и связанных параметров в операторах PARF и PARC с помощью оператора:

CC(*) = кс1,кс2,...,ксn;

или

CC(к1-к2) = кск1,...,кск2;

или

CC(к1,к2) = кск1,кск2;

где n - общее число коэффициентов связи;

кс1,кс2,кск1,кск2,ксn - коэффициенты связи между пс1 и пз1,

пс2 и пз2, пск1 и пзк1, пск2 и пзк2, псn и пзn соответственно.

Какими способами можно пересчитать окуляр на другую величину фокусного расстояния.

Изменение масштаба

С помощью изменения радиусов кривизн

С помощью изменения альфа

Подгонка характеристик-заднее фокусное расстояние-радиус/осевое расстояние (лучше радиус).

Допустим у нас окуляр Кельнера (() () фокусное расстояние равно 56мм, надо получить окуляр с фокусным расстоянием 80мм, что можно сделать? (Окуляр рассчитывается в обратном ходе лучей)

1) Масштабирование делим 80 на 56 и получаем коэффициент масштабирования, недостаток такого метода в том, что изменяются осевые расстояния и кривизны. Кривизны все гостированны поэтому приводя их к госту всё поплывет, осевые расстояния могут получиться с точностью до черти какого знака и их тяжело выдержать. Достоинства: (простота?)

2) Можно изменить одну кривизну или одно осевое расстояние, путем подгонки характеристик: Подгонка характеристик-заднее фокусное расстояние-радиус/осевое расстояние (лучше радиус). В случае окуляра Кельнера имеет смысл изменить осевое расстояние D3 (между склейкой и одиночной линзой). Недостаток в случае изменения осевого расстояния оно может стать отрицательным, либо увеличиться до такого расстояния, что луч не пройдет. В случае радиуса кривизны он может стать слишком маленьким и толщины линзы может не хватить будет пересечение поверхностей (типо того)

3) Изменение альфа: Настроить-поверхности-углами нулевого луча, в появившемся окне вписываем требуемое фокусное расстояние в «H 1» в «alf 0» оставляем ноль, чтобы текущее фокусное расстояние стало искомым требуется, чтобы последняя альфа была равна единице. (по сути урезанный предыдущий способ, так например если изменить только последнюю альфу и по прошлому методу изменять кривизну последней поверхности получится тоже самое).

4) Оптимизация:

PAR(*)=… // варьируемые параметры

EQF(*)=VG0;

EQF#(*)=-80 //требуемое фокусное расстояние (минус из-за того что это передний фокус)

Недостаток в том что заранее тяжело сказать что станет с системой, но зато можно совместить изменение фокуса непосредственно с оптимизацией.

Билет 13

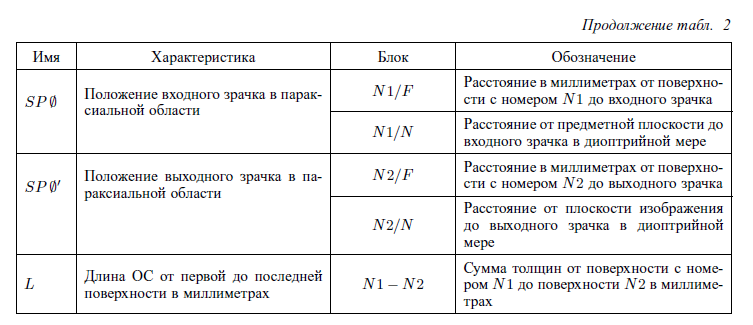
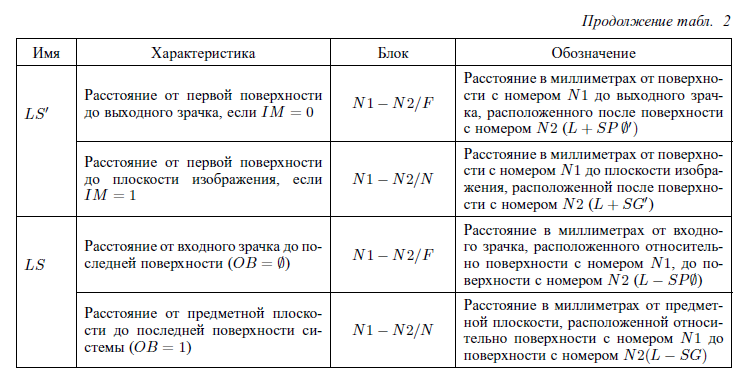
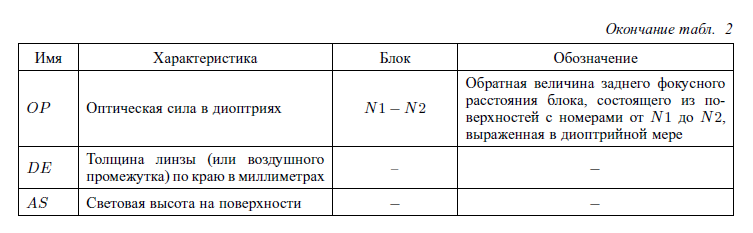
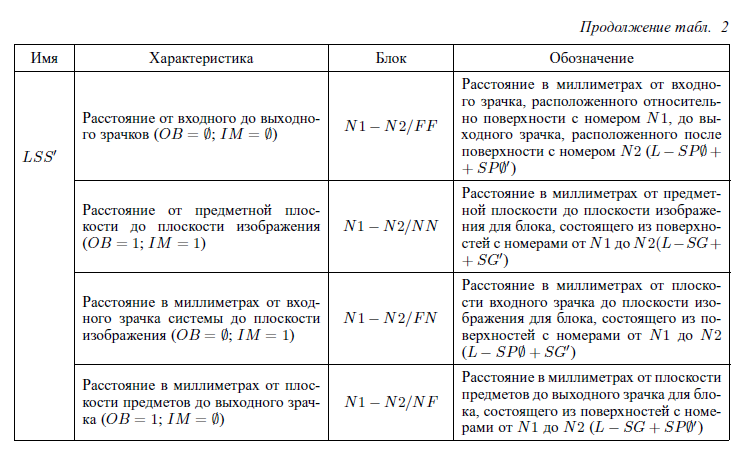
Марки параксиальных характеристик

┌──────┬──────────┬─────────────────────────────────────────────────┐

│ имя │указа- │ характеристика │

│ │тели │ │

├──────┼──────────┼─────────────────────────────────────────────────┤

│ V0 │ │ Обобщенное увеличение в заданной плоскости │

│ │ │ оптической системы │

│ VG0 │ N1*N2/пи │ Обобщенное увеличение в плоскости Гаусса │

│ SG │ N1/п │ Положение плоскости предмета для блока │

│ SG' │ N2/и │ Положение плоскости Гаусса │

│ DSG' │ │ Смещение плоскости Гаусса относительно заданной │

│ │ │ в оптической системе │

│ SP0 │ N1/п │ Положение входного зрачка │

│ SP0' │ N2/и │ Положение выходного зрачка │

│ L │ N1*N2 │ Сумма толщин с N1 по N2 │

│ LS' │ N1*N2/и │ L + SG' (L + SP0') │

│ LS │ N1*N2/п │ L - SG (L - SP0) │

│ LSS' │ N1*N2/пи │ L - SG + SG' │

│ │ │ (L-SP0+SG' или L-SG+SP0' или L-SP0+SP0') │

│ OP │ N1*N2 │ Оптическая сила в дптр. │

│ DE │ │ Толщины "по краю" │

│ AS │ │ Световые высоты │

│ ID │ K │ Функция светораспределения для K-ого пучка │

└──────┴──────────┴─────────────────────────────────────────────────┘

Тут имеет смысл посмотреть в приложение, таблицу 2

Какими способами можно пересчитать 2-х линзовый объектив на другое фокусное расстояние.

Подгонка характеристик-заднее фокусное расстояние-радиус/осевое расстояние (лучше радиус).

Допустим у нас объектив с фокусным расстоянием равным 56мм, надо получить объектив с фокусным расстоянием 80мм, что можно сделать?

5) Масштабирование делим 80 на 56 и получаем коэффициент масштабирования, недостаток такого метода в том, что изменяются осевые расстояния и кривизны. Кривизны все гостированны поэтому приводя их к госту всё поплывет, осевые расстояния могут получиться с точностью до черти какого знака и их тяжело выдержать. Достоинства: (простота?)

6) Можно изменить одну кривизну или одно осевое расстояние, путем подгонки характеристик: Подгонка характеристик-заднее фокусное расстояние-радиус/осевое расстояние (лучше радиус). Недостаток в случае изменения осевого расстояния оно может стать отрицательным, либо увеличиться до черти каких размеров. В случае радиуса кривизны он может стать слишком маленьким и толщины линзы может не хватить будет пересечение поверхностей ((типо того))

7) Изменение альфа: Настроить-поверхности-углами нулевого луча, в появившемся окне вписываем требуемое фокусное расстояние в «H 1» в «alf 0» оставляем ноль, чтобы текущее фокусное расстояние стало искомым требуется, чтобы последняя альфа была равна единице. (по сути урезанный предыдущий способ, так например если изменить только последнюю альфу и по прошлому методу изменять кривизну последней поверхности получится тоже самое).

8) Оптимизация:

PAR(*)=… // варьируемые параметры

EQF(*)=VG0;

EQF#(*)=-80 //требуемое фокусное расстояние (минус из-за того что это передний фокус)

таблица 3

┌──────┬──────────┬────────────────────────────────────┐

│указа-│допустимые│ тип аберрации │

│ тель │ значения │ │

├──────┼──────────┼────────────────────────────────────┤

│ L │0,1,2,3,4 │ 0 -аберрация основной длины волны │

│ приз-│ ',",* │ 1,2,3,4, - аберрации │

│ нак │ │ 1-ой,2-ой,3-й,4-ой │

│хрома-│ │ дополнительных длин волн │

│тизма │ │ соответственно │

│ │ │ ' -(апостроф)-хроматическая │

│ │ │ разность аберраций для крайних │

│ │ │ дополнительных длин волн; │

│ │ │ " -(кавычки)-хроматическая │

│ │ │ аберрация вторичного спектра; │

│ │ │ * -символ размножения марки на │

│ │ │ марки со значениями 0,1...nl │

│ │ │ где nl - число длин волн. │

│ │ │ │

│ J │ 0,1,2,3, │ 0,1,2,3,4,5 -аберрация │

│номер │ 4,5,* │ 1-го,2-го, и т.д.пучка в │

│пучка │ │ соответствии с массивом в(J) │

│ │ │ относительных высот предмета; │

│ │ │ * -символ размножения марки со │

│ │ │ значениями индекса J=0,J=1 и │

│ │ │ т.д. в зависимости от │

│ │ │ количества внеосевых пучков; │

│ │ │ │

│ I │1,2,3,4,* │ 1,2,3,4 -аберрация │

│номер │ │ 1-го,2-го, и т.д.луча в │

│луча в│ │ половине сечения осевого или │

│ 1/2 │ │ J-го внеосевго пучка,в соот- │

│сече- │ │ ветствии с массивами относи- │

│ния │ │ тельных высот лучей │

│ │ │ * - символ размножения марки с │

│ │ │ индексами I=1,I=2, и т.д.до │

│ │ │ значения I=RAYA,I=RAYM,I=RAYS │

│ │ │ или I=RAYT, в зависимости от │

│ │ │ типа аберрации │

│ │ │ │

│ S │U,D,* │ U -аберрации верхней половины │

│указа-│ │ сечения пучка; │

│тель │ │ D -аберрации нижней половины │

│сече- │ │ сечения пучка; │

│ния │ │ * -символ размножения марки │

└──────┴──────────┴────────────────────────────────────┘

VG0/n1-n2/FN0

│ │ │││ номер состояния

номер начальной поверхности │ │ ││└──────────────────────────

─────────────────────────────┘ │ ││

│ ││ ┌─ F - дальний

номер конечной поверхности │ ││ тип изображения ─┴─ N - ближний

─────────────────────────────────┘ │└───────────────────────────

│

│ ┌─ F - дальний

│ тип предмета ─┴─ N - ближний

└────────────────────────────

Касательно OB и IM… 1 - это конечное расстояние 0 – это бесконечность

Дата добавления: 2015-10-23; просмотров: 95 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
Указатели см таблицу 3	\|	равноточных наблюдений при прямых измерениях.

mybiblioteka.su - 2015-2024 год. (0.063 сек.)