
Читайте также:
|
Наибольшим общим делителем (НОД) двух чисел u и v называется такое наибольшее целое число НОД(u, v), которое делит оба числа u и v.
Прямой метод нахождениянаибольшего общего делителя (НОД) состоит в разложении чисел u и v на простые множители и выборе среди них всех общих множителей. Эта задача является сложной, поскольку требует для своего выполнения числа операций, экспоненциально зависящего от числа разрядов чисел u и v. Однако существует быстрый метод вычисления НОД. Он основан на алгоритме Евклида и состоит в следующем. Пусть, не умаляя общности, u > v > 0. Тогда производятся вычисления
| u | = a 1 v + b 1 | b 1 | = res v u | 0 £ b 1< v | |
| v | = a 2 b 1 + b 2 | b 2 | = 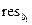 v v
| 0 £ b 2< b 1 | |
| b 1 | = a 3 b 2 + b 3 | b 3 | =  b 1 b 1
| 0 £ b 3 < b 2 | |
| … bk – 2 | … = ak bk – 1+ bk | … bk | …
=  bk – 2 bk – 2
| … 0 £ bk < bk – 1 |
до тех пор, пока не будет получено, что bk = 0 или bk = 1. Если bk = 1, то НОД(u, v) = 1, т.е. u и v взаимно простые числа. Иначе, когда bk = 0, имеем НОД(u, v) = bk – 1, т.е. bk – 1 и дает решение задачи. Сложность данного алгоритма полиномиально зависит от числа разрядов u и v и требует 0 (log v) делений.
Обращение элементов по модулю n
Элемент a обратный к элементу a по модулю n (записывается a = a –1 mod n) – это такое целое число a, которое удовлетворяет уравнению
a a = 1 mod n.
Для целых чисел a и n решение данной задачи (называемой решением сравнения) существует не всегда, а только при условии, что НОД чисел a и n равен единице. В частности, обратный элемент a существует всегда, когда a строго меньше n и само n простое число.
В тех случаях, когда обратный элемент существует, его нахождение является простой задачей. Решается она с помощью алгоритма Евклида. Действительно, если проанализировать алгоритм Евклида, можно видеть, что он дает возможность не только вычислить НОД чисел a и n, но и представить его в следующей форме:
НОД(a, n) = x a + y n,
где x и y – целые (не обязательно положительные) числа. Поскольку предполагается, что обратный элемент существует, должно быть выполнено условие НОД(a, n) = 1, или
x a + y n =1mod n.
Но y n =0mod n, поскольку произведение y n кратно n. В силу этого
a –1 = x mod n.
Дата добавления: 2015-10-26; просмотров: 113 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Особенности асимметричных криптосистем | | | Основы построения асимметричных систем |